- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Логические операции компьютеров презентация
Содержание
- 1. Логические операции компьютеров
- 2. Логические операции инверсия конъюнкция дизъюнкция импликация эквивалентность исключающее или
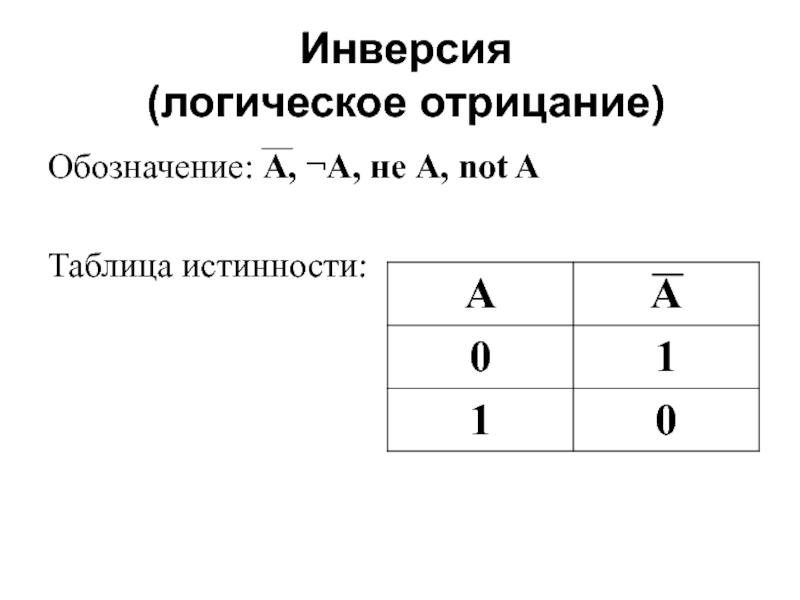
- 3. Инверсия (логическое отрицание) Обозначение: A, ¬А,
- 4. Конъюнкция (логическое умножение) Обозначение: A&B, A∧B, А⋅В,
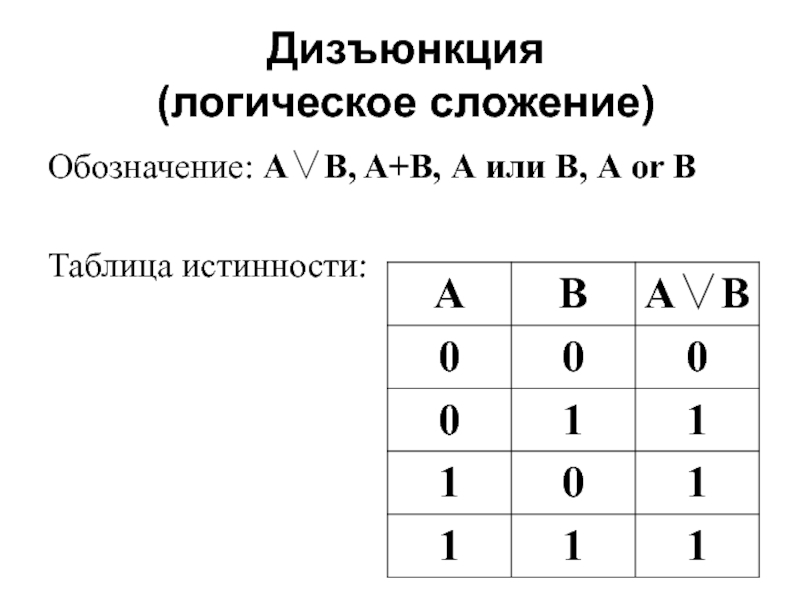
- 5. Дизъюнкция (логическое сложение) Обозначение: A∨B, A+B, А
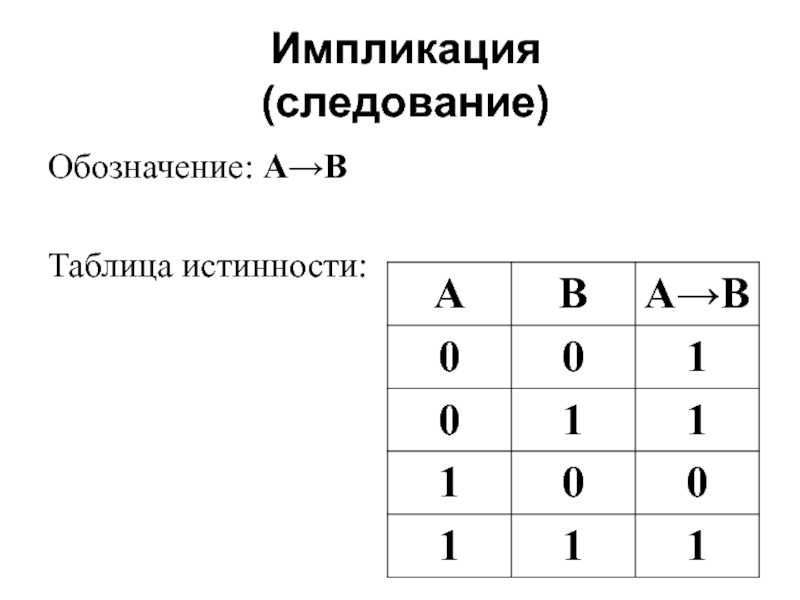
- 6. Импликация (следование) Обозначение: A→B Таблица истинности:
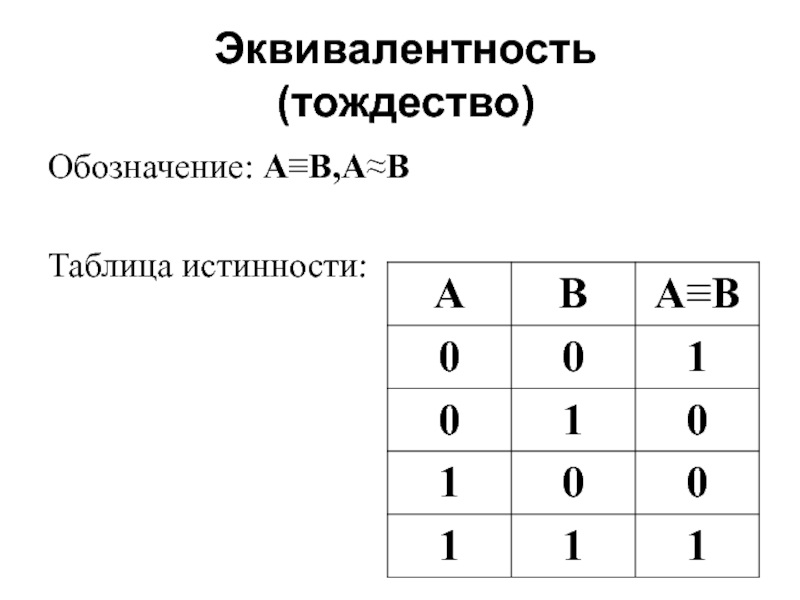
- 7. Эквивалентность (тождество) Обозначение: A≡B,А≈В Таблица истинности:
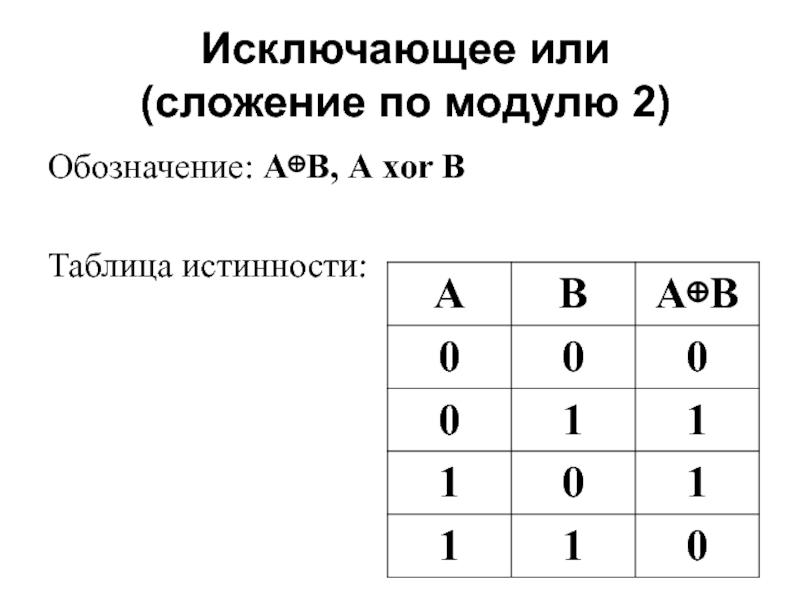
- 8. Исключающее или (сложение по модулю 2) Обозначение:
- 9. Приоритет логических операций инверсия конъюнкция дизъюнкция импликация эквивалентность исключающее или
- 10. Алгоритм составления таблиц истинности 1. Посчитать
- 11. Выполните задание Сколько различных решений имеет система
- 13. Решение системы логических уравнений Метод отображений Е.В.Хламов, Е.А.Мирончик
- 14. Выполните задание Сколько различных решений имеет система
- 15. Алгоритм решения 1. Составить таблицу истинности к
- 16. Алгоритм решения 2. Выписать такие наборы переменных,
- 17. Алгоритм решения 2. Выписать такие наборы переменных,
- 18. Алгоритм решения 2. Дописать вверху таблицы переменные
- 19. Алгоритм решения 2. Выделить в таблице значения
- 20. Алгоритм решения 3. Определить количество одинаковых переменных,
- 21. Алгоритм решения 3. Записать все возможные комбинации
- 22. Алгоритм решения 3. Выписать из таблицы все
- 23. Алгоритм решения 4. Составить итоговую таблицу
- 24. Алгоритм решения 4. Заполнить первую строку итоговой
- 25. Алгоритм решения 4. Заполнить оставшиеся строки таблицы
- 26. Алгоритм решения 4. Заполнить оставшиеся строки таблицы
- 27. Алгоритм решения 5. Сложить все значения последней
- 28. Задание для самостоятельного решения Сколько различных решений
- 29. Эталон решения 1.
- 30. Задание для работы в парах Сколько различных
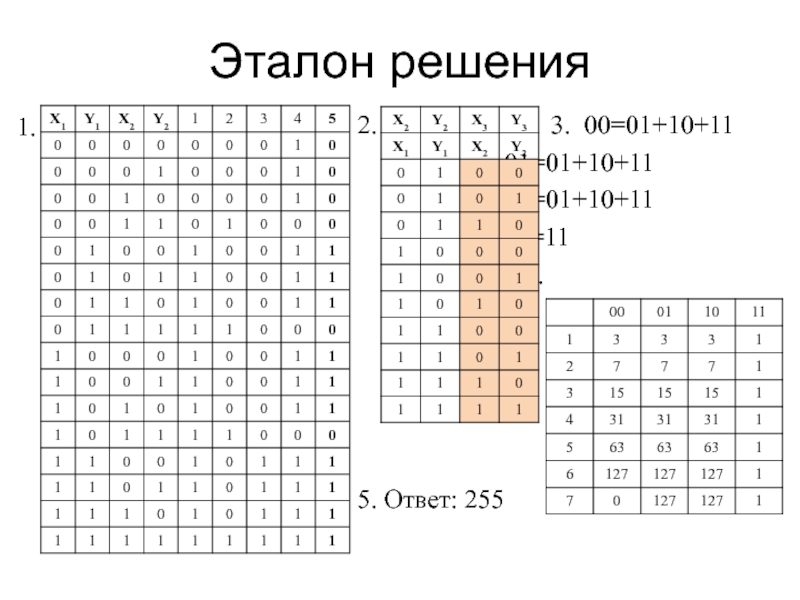
- 31. Эталон решения 2.
- 32. Задание для индивидуальной работы Сколько различных решений
- 33. Эталон решения 1.
- 34. сегодня я узнал … было трудно… я понял, что… я научился… я смог… меня удивило…
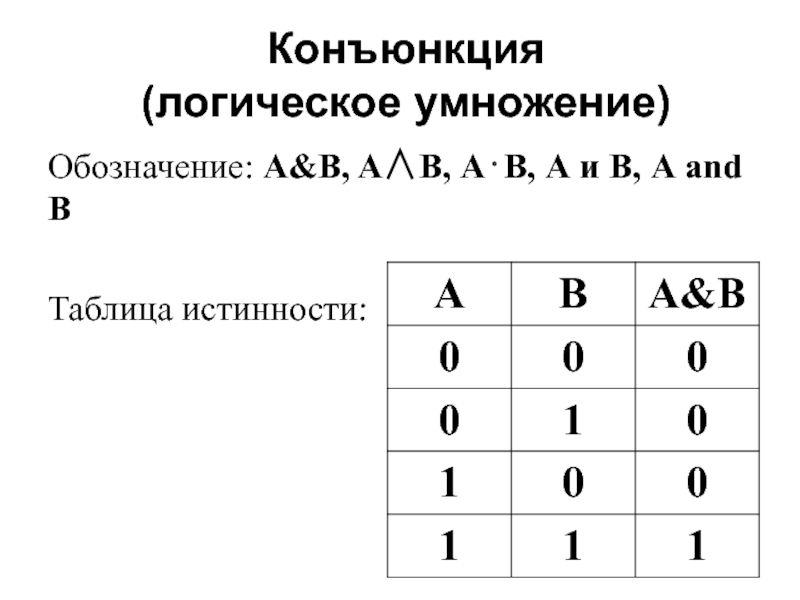
Слайд 4Конъюнкция
(логическое умножение)
Обозначение: A&B, A∧B, А⋅В, А и В, А and В
Таблица
истинности:
Слайд 9Приоритет логических операций
инверсия
конъюнкция
дизъюнкция
импликация
эквивалентность
исключающее или
Слайд 10
Алгоритм составления таблиц истинности
1. Посчитать количество переменных (n) в логическом выражении.
2. Определить
число строк в таблице, которое равно m=2n .
3. Посчитать количество логических операций и определить количество столбцов в таблице, которое равно: количество переменных + количество операций.
4. Ввести название столбцов в таблицу в соответствие с последовательностью выполнения логических операций с учетом скобок и приоритетов.
5. Заполнить столбцы входных переменных наборами значений.
6. Провести заполнение таблицы истинности по столбцам, выполняя логические операции.
3. Посчитать количество логических операций и определить количество столбцов в таблице, которое равно: количество переменных + количество операций.
4. Ввести название столбцов в таблицу в соответствие с последовательностью выполнения логических операций с учетом скобок и приоритетов.
5. Заполнить столбцы входных переменных наборами значений.
6. Провести заполнение таблицы истинности по столбцам, выполняя логические операции.
Слайд 11Выполните задание
Сколько различных решений имеет система уравнений
(X1 ≡ X2) →
(X2 ≡ X3) = 1
(X2 ≡ X3) → (X3 ≡ X4) = 1
...
(X5 ≡ X6) → (X6 ≡ X7) = 1
где x1, x2, …, x7 – логические переменные?
В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство.
В качестве ответа нужно указать количество таких наборов.
(X2 ≡ X3) → (X3 ≡ X4) = 1
...
(X5 ≡ X6) → (X6 ≡ X7) = 1
где x1, x2, …, x7 – логические переменные?
В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство.
В качестве ответа нужно указать количество таких наборов.
Слайд 14Выполните задание
Сколько различных решений имеет система уравнений
(X1 ≡ X2) →
(X2 ≡ X3) = 1
(X2 ≡ X3) → (X3 ≡ X4) = 1
...
(X5 ≡ X6) → (X6 ≡ X7) = 1
где x1, x2, …, x7 – логические переменные?
В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство.
В качестве ответа нужно указать количество таких наборов.
(X2 ≡ X3) → (X3 ≡ X4) = 1
...
(X5 ≡ X6) → (X6 ≡ X7) = 1
где x1, x2, …, x7 – логические переменные?
В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство.
В качестве ответа нужно указать количество таких наборов.
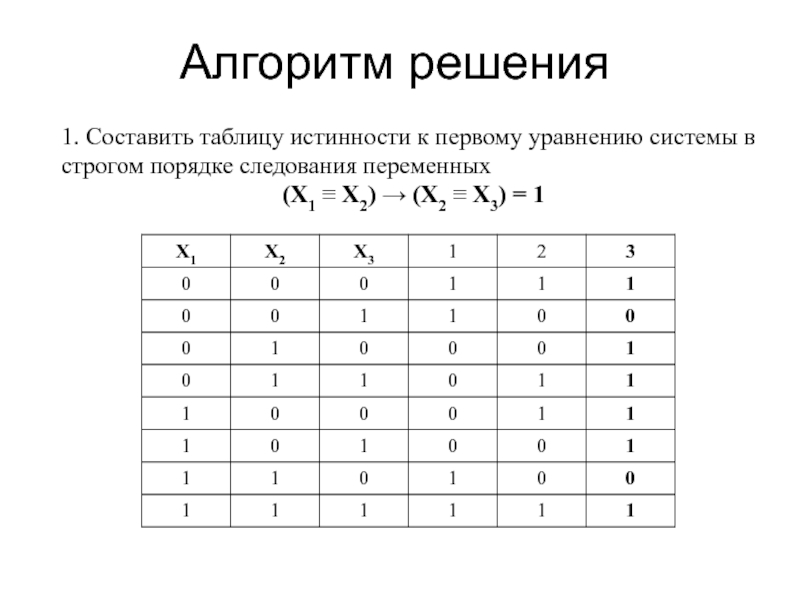
Слайд 15Алгоритм решения
1. Составить таблицу истинности к первому уравнению системы в строгом
порядке следования переменных
(X1 ≡ X2) → (X2 ≡ X3) = 1
(X1 ≡ X2) → (X2 ≡ X3) = 1
Слайд 16Алгоритм решения
2. Выписать такие наборы переменных, которые приводят в результате к
получению «1».
(X1 ≡ X2) → (X2 ≡ X3) = 1
(X1 ≡ X2) → (X2 ≡ X3) = 1
Слайд 17Алгоритм решения
2. Выписать такие наборы переменных, которые приводят в результате к
получению «1».
(X1 ≡ X2) → (X2 ≡ X3) = 1
(X1 ≡ X2) → (X2 ≡ X3) = 1
Слайд 18Алгоритм решения
2. Дописать вверху таблицы переменные второго уравнения, стоящие на соответствующих
местах
(X1 ≡ X2) → (X2 ≡ X3) = 1
(X2 ≡ X3) → (X3 ≡ X4) = 1
(X1 ≡ X2) → (X2 ≡ X3) = 1
(X2 ≡ X3) → (X3 ≡ X4) = 1
Слайд 19Алгоритм решения
2. Выделить в таблице значения переменных, которые встречаются в обоих
уравнениях
(X1 ≡ X2) → (X2 ≡ X3) = 1
(X2 ≡ X3) → (X3 ≡ X4) = 1
(X1 ≡ X2) → (X2 ≡ X3) = 1
(X2 ≡ X3) → (X3 ≡ X4) = 1
Слайд 20Алгоритм решения
3. Определить количество одинаковых переменных, встречающихся в обоих уравнениях. В
данных уравнениях
их 2 (X2, X3).
(X1 ≡ X2) → (X2 ≡ X3) = 1
(X2 ≡ X3) → (X3 ≡ X4) = 1
их 2 (X2, X3).
(X1 ≡ X2) → (X2 ≡ X3) = 1
(X2 ≡ X3) → (X3 ≡ X4) = 1
Слайд 22Алгоритм решения
3. Выписать из таблицы все комбинации второго уравнения (в красной
рамке), соответствующие строкам таблицы первого уравнения (оранжевое). Количество выписанных комбинаций должно совпадать с количеством строк таблицы (6 строк).
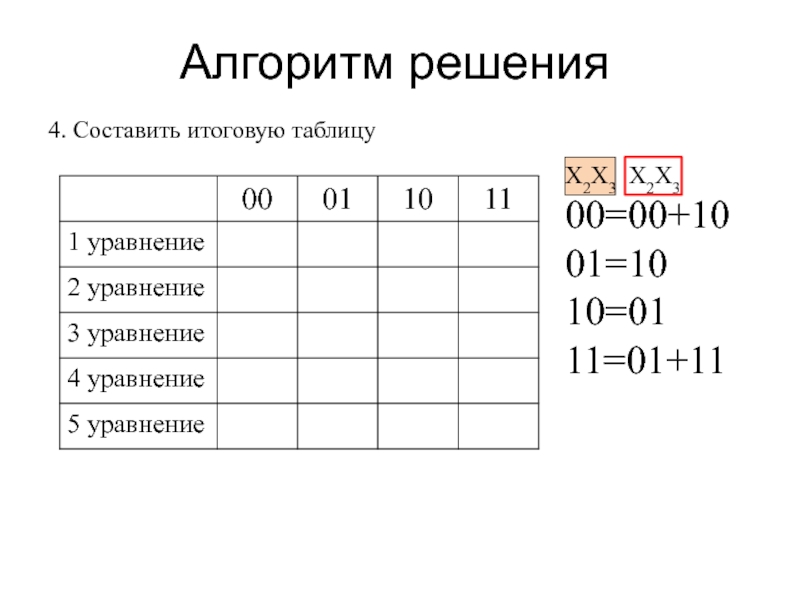
Слайд 24Алгоритм решения
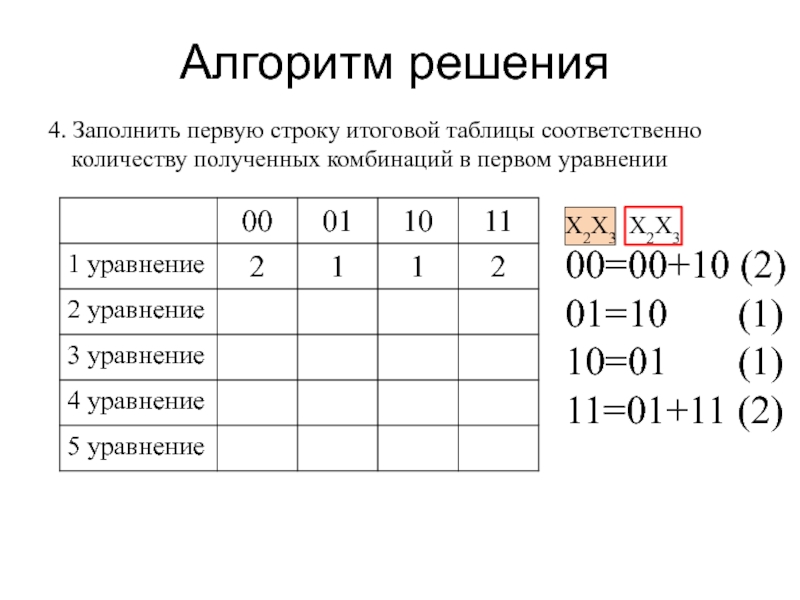
4. Заполнить первую строку итоговой таблицы соответственно количеству полученных комбинаций
в первом уравнении
Слайд 25Алгоритм решения
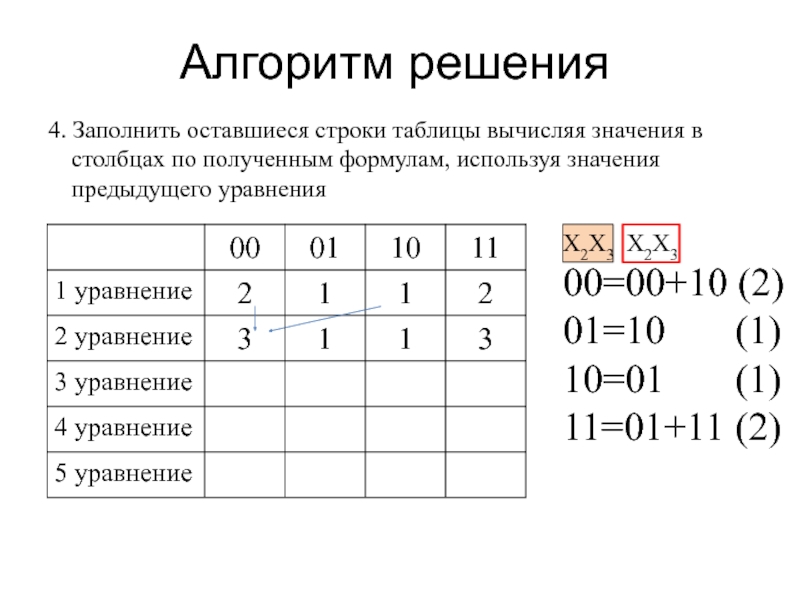
4. Заполнить оставшиеся строки таблицы вычисляя значения в столбцах по
полученным формулам, используя значения предыдущего уравнения
Слайд 26Алгоритм решения
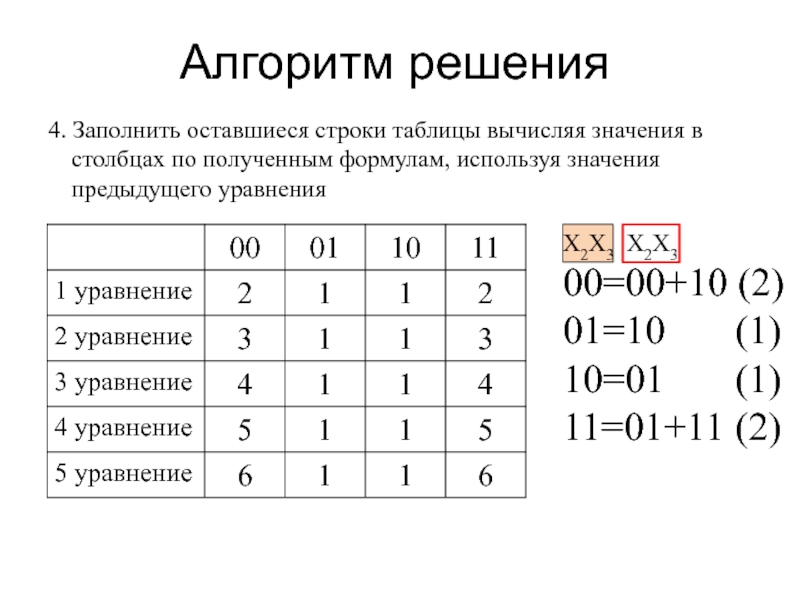
4. Заполнить оставшиеся строки таблицы вычисляя значения в столбцах по
полученным формулам, используя значения предыдущего уравнения
Слайд 28Задание для самостоятельного решения
Сколько различных решений имеет система уравнений
(x1 ≡
¬x2) ∧ (¬x1 ≡ x3) = 0
(x2 ≡ ¬x3) ∧ (¬x2 ≡ x4) = 0
...
(x7 ≡ ¬x8) ∧ (¬x7 ≡ x9) = 0
где x1, x2, …, x9 – логические переменные?
В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство.
В качестве ответа нужно указать количество таких наборов.
(x2 ≡ ¬x3) ∧ (¬x2 ≡ x4) = 0
...
(x7 ≡ ¬x8) ∧ (¬x7 ≡ x9) = 0
где x1, x2, …, x9 – логические переменные?
В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство.
В качестве ответа нужно указать количество таких наборов.
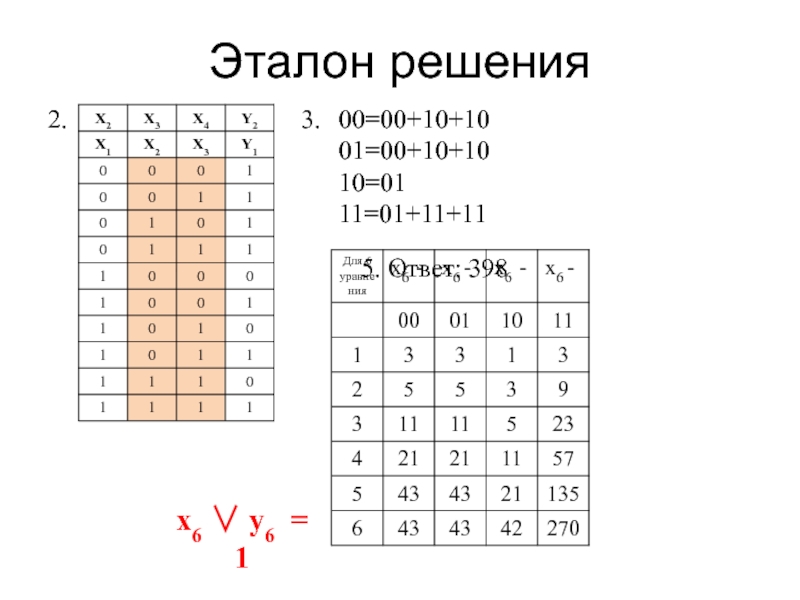
Слайд 30Задание для работы в парах
Сколько различных решений имеет система уравнений
(x1
∧ x2 → x3) ∧ (x1 ∨ y1) = 1
(x2 ∧ x3 → x4) ∧ (x2 ∨ y2) = 1
(x3 ∧ x4 → x5) ∧ (x3 ∨ y3) = 1
(x4 ∧ x5 → x6) ∧ (x4 ∨ y4) = 1
(x5 ∧ x6 → x7) ∧ (x5 ∨ y5) = 1
x6 ∨ y6 = 1
где x1, x2, …, x6, y1, y2, …, y6, – логические переменные?
В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство.
В качестве ответа нужно указать количество таких наборов.
(x2 ∧ x3 → x4) ∧ (x2 ∨ y2) = 1
(x3 ∧ x4 → x5) ∧ (x3 ∨ y3) = 1
(x4 ∧ x5 → x6) ∧ (x4 ∨ y4) = 1
(x5 ∧ x6 → x7) ∧ (x5 ∨ y5) = 1
x6 ∨ y6 = 1
где x1, x2, …, x6, y1, y2, …, y6, – логические переменные?
В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство.
В качестве ответа нужно указать количество таких наборов.
Слайд 32Задание для индивидуальной работы
Сколько различных решений имеет система уравнений
(x1 ∨
y1) ∧ ((x2 ∧ y2) → (x1 ∧ y1)) = 1
(x2 ∨ y2) ∧ ((x3 ∧ y3) → (x2 ∧ y2)) = 1
...
(x6 ∨ y6) ∧ ((x7 ∧ y7) → (x6 ∧ y6)) = 1
x7 ∨ y7 = 1
где x1, x2, …, x6, y1, y2, …, y6, – логические переменные?
В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство.
В качестве ответа нужно указать количество таких наборов.
(x2 ∨ y2) ∧ ((x3 ∧ y3) → (x2 ∧ y2)) = 1
...
(x6 ∨ y6) ∧ ((x7 ∧ y7) → (x6 ∧ y6)) = 1
x7 ∨ y7 = 1
где x1, x2, …, x6, y1, y2, …, y6, – логические переменные?
В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство.
В качестве ответа нужно указать количество таких наборов.