- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекція №5. Закони розподілу випадкових величин презентация
Содержание
- 1. Лекція №5. Закони розподілу випадкових величин
- 2. ЗМІСТ Рівномірний розподіл Нормальний розподіл
- 3. Рівномірний розподіл Рівномірний розподіл. Розподіл ймовірностей називають
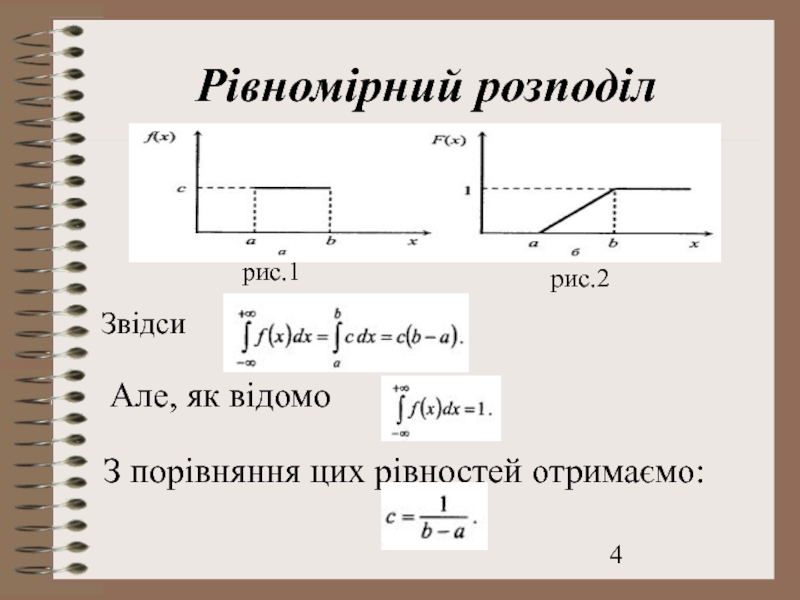
- 4. Рівномірний розподіл Звідси Але, як відомо З порівняння цих рівностей отримаємо: рис.1 рис.2
- 5. Рівномірний розподіл Отже щільність ймовірностей неперервної випадкової
- 6. Рівномірний розподіл Наведемо приклади деяких конкретних величин
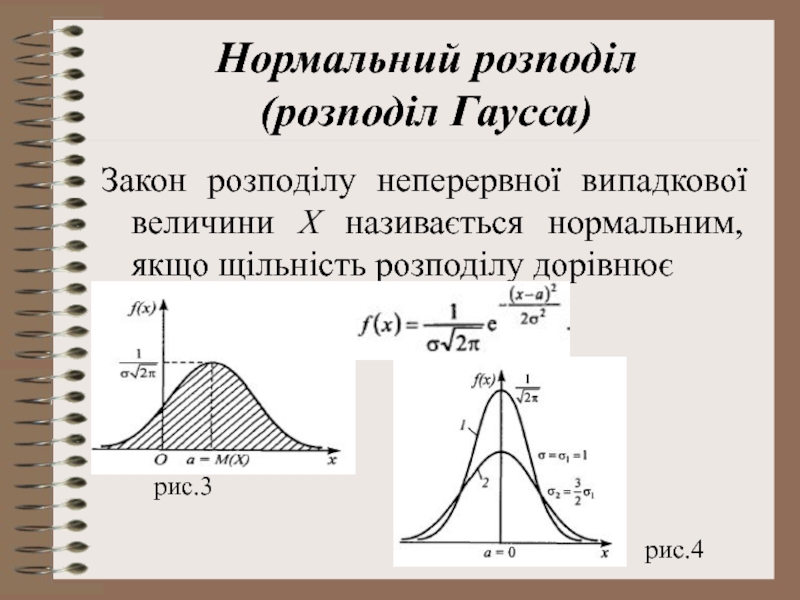
- 7. Нормальний розподіл (розподіл Гаусса) Закон розподілу
- 8. Нормальний розподіл (розподіл Гаусса) Графік розподілу
- 9. Нормальний розподіл (розподіл Гаусса) При збільшені
- 10. Нормальний розподіл (розподіл Гаусса) Щільність розподілу
- 11. Функція Лапласа Припустимо, що випадкова величина Х
- 12. Функція Лапласа Отриманий інтеграл не береться в
- 13. Функція Лапласа Основні властивості функції Лапласа З
- 14. Функція Лапласа Згідно з та з урахуванням виконаної раніше підстановки
- 15. Розподіл “х - квадрат” Припустимо, -
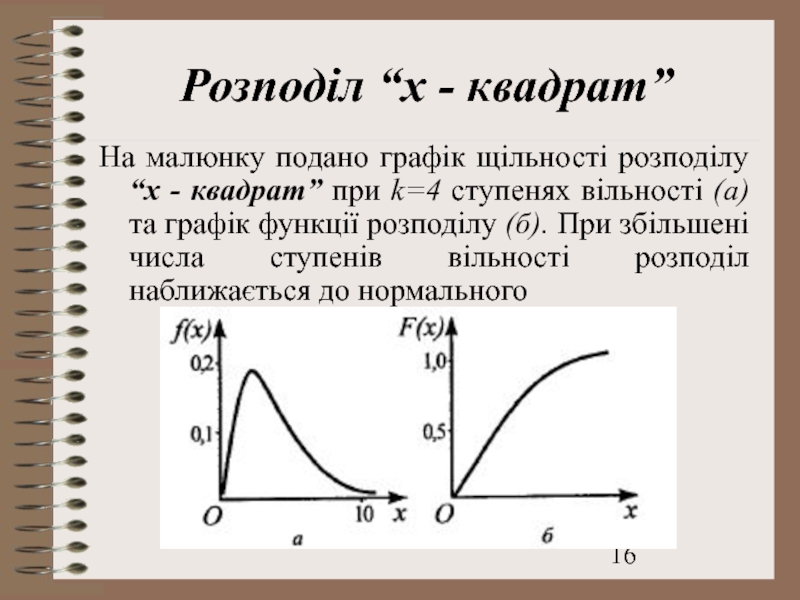
- 16. Розподіл “х - квадрат” На малюнку подано
- 17. Розподіл Стьюдента Припустимо що Z – нормально
- 18. Розподіл Стьюдента Розподіл Стьюдента повністю визначається числом
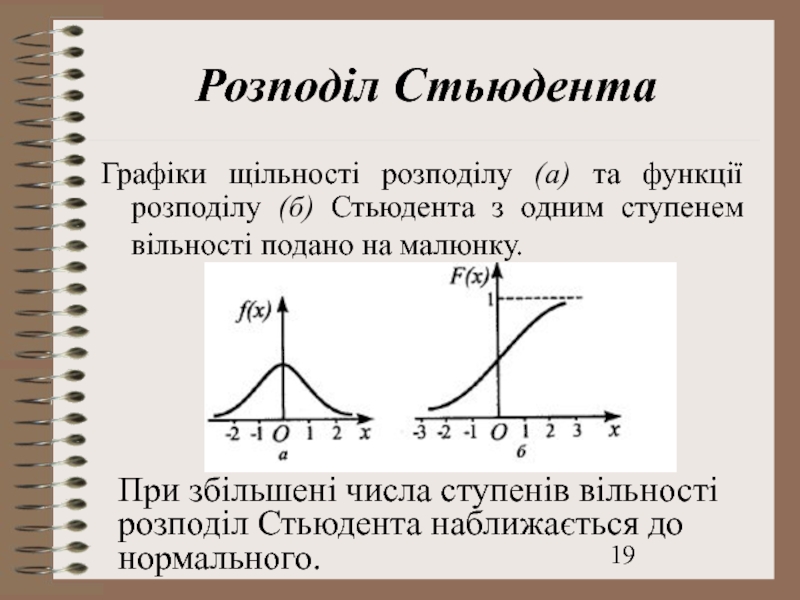
- 19. Розподіл Стьюдента Графіки щільності розподілу (а) та
- 20. ДЯКУЮ ЗА УВАГУ
Слайд 2ЗМІСТ
Рівномірний розподіл
Нормальний розподіл
(розподіл Гаусса)
Розподіл “х - квадрат”
Розподіл
Слайд 3Рівномірний розподіл
Рівномірний розподіл. Розподіл ймовірностей називають рівномірним, якщо на проміжку (а,в),
Слайд 5Рівномірний розподіл
Отже щільність ймовірностей неперервної випадкової величини Х, яка рівномірно розподілена
Інтегральна функція розподілу F(x) для рівномірно розподіленої величини на проміжку
ЇЇ графік зображено на рис.2
Слайд 6Рівномірний розподіл
Наведемо приклади деяких конкретних величин з рівномірним законом розподілу. При
Слайд 7Нормальний розподіл
(розподіл Гаусса)
Закон розподілу неперервної випадкової величини Х називається нормальним,
рис.3
рис.4
Слайд 8Нормальний розподіл
(розподіл Гаусса)
Графік розподілу Гаусса описується симетричною відносно а =
При х=а ордината кривої нормальної щільності ймовірності дорівнює
Слайд 9Нормальний розподіл
(розподіл Гаусса)
При збільшені квадратичного відхилення ця ордината зменшується. При
Нормальний розподіл з параметрами а=0 та
=1 називають стандартним (нормованим)
Слайд 10Нормальний розподіл
(розподіл Гаусса)
Щільність розподілу в такому випадку дорівнює:
Значення функції
наведені
а графік зображено на рис.4 інтегральна функція
Розподілу має вигляд
Слайд 11Функція Лапласа
Припустимо, що випадкова величина Х розподілена нормальним законом. Тоді ймовірність
Зробимо підстановку
Тоді
Функція щільності нормально розподіленої величини набуде при цьому нормованого виду і ми матимемо:
Слайд 12Функція Лапласа
Отриманий інтеграл не береться в елементарних функціях, тому для його
яка називається функцією Лапласа (інтегралом ймовірностей)
Слайд 13Функція Лапласа
Основні властивості функції Лапласа
З допомогою функції Лапласа можна знайти ймовірність
Слайд 15Розподіл “х - квадрат”
Припустимо,
- нормально
розподілені незалежні випадкові величини, математичне сподівання
має розподіл
з k=n ступенями вільності
Якщо ж ці величини пов'язані між собою декількома (наприклад m) лінійними співвідношеннями, то число ступенів вільності k = n - m
Слайд 16Розподіл “х - квадрат”
На малюнку подано графік щільності розподілу “х -
Слайд 17Розподіл Стьюдента
Припустимо що Z – нормально розподілена нормована випадкова величина
a
Слайд 18Розподіл Стьюдента
Розподіл Стьюдента повністю визначається числом ступенів вільності і є парною
де
- коефіцієнт, який залежить від
об'єму вибірки.
Слайд 19Розподіл Стьюдента
Графіки щільності розподілу (а) та функції розподілу (б) Стьюдента з
При збільшені числа ступенів вільності розподіл Стьюдента наближається до нормального.