- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 6. Численное интегрирование функций презентация
Содержание
- 1. Лекция 6. Численное интегрирование функций
- 2. Численное интегрирование функций Подходы: замена исходной функции
- 3. Вероятностные (статистические) методы Пример: задан шар
- 4. Вероятностные (статистические) методы В пределе
- 5. Методы с подбором узлов На отрезке [–1,1]
- 6. Интегрирование интерполирующих полиномов При замене f (x)
- 7. Интегрирование интерполирующих полиномов При замене f (x)
- 8. Интегрирование интерполирующих полиномов Формулы прямоугольников: левосторонних; правосторонних;
- 9. Формула левосторонних прямоугольников На отрезке [xi, xi+1]
- 10. Формула левосторонних прямоугольников
- 11. Формула правосторонних прямоугольников На отрезке [xi, xi+1]
- 12. Формула правосторонних прямоугольников
- 13. Формула центральных прямоугольников На отрезке [xi, xi+1]
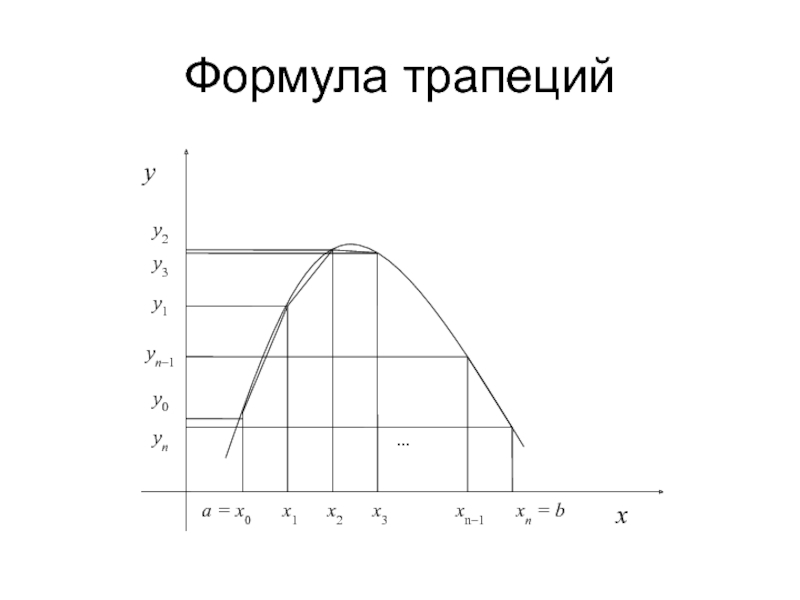
- 14. Формула трапеций На отрезке [xi, xi+1] полагаем
- 15. Формула трапеций На отрезке [a, b]
- 16. Формула трапеций
- 17. Квадратурные формулы Вспомним формулу Выполним
- 18. Квадратурные формулы Если предположить, что cij =
- 19. Квадратурные формулы Если Pi(x) = Lp,i(x), т.е.
- 20. Квадратурные формулы Тогда Для p
- 21. Квадратурные формулы Интегрируем:
- 22. Квадратурные формулы В итоге
- 23. Квадратурные формулы Для p = 2 имеем:
- 24. Квадратурные формулы Интегрируем:
- 25. Квадратурные формулы В итоге получим:
- 26. Квадратурные формулы Для отрезка [a, b]
- 27. Квадратурные формулы Если сетка равномерная, то
- 28. Квадратурные формулы Интерполирующий полином
- 29. Квадратурные формулы Тогда
- 30. Коэффициенты Ньютона-Котеса В случае равномерной сетки положим
- 31. Коэффициенты Ньютона-Котеса Свойства коэффициентов Ньютона-Котеса:
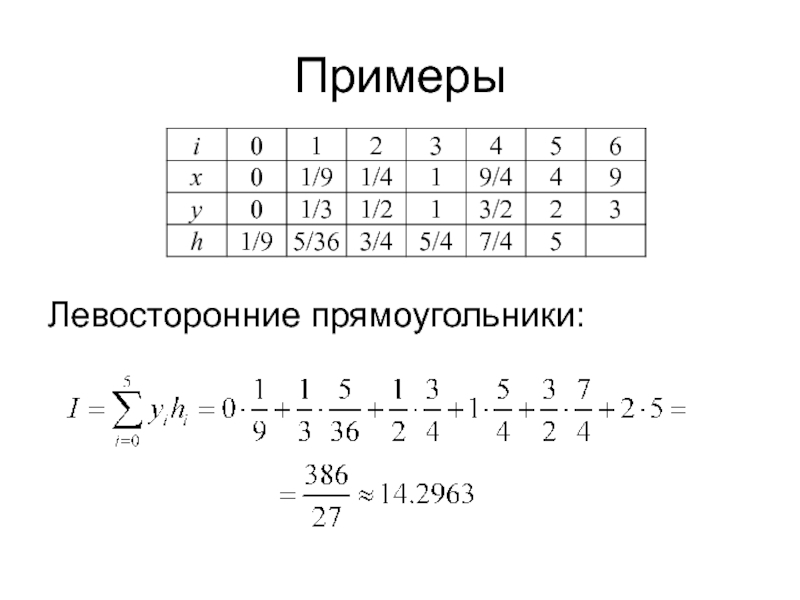
- 32. Примеры n = 6
- 33. Примеры Левосторонние прямоугольники:
- 34. Примеры Правосторонние прямоугольники:
- 35. Примеры Трапеции:
- 36. Примеры Формула Симпсона:
- 37. Примеры Формула Симпсона:
- 38. Примеры Точность интегрирования:
Численное интегрирование функций Подходы: замена исходной функции f (x) (заданной таблично или аналитически) интерполирующим полиномом P(x) с известной первообразной; подбор оптимальных узлов интегрирования при аналитически заданной функции f (x); вероятностные или
Слайд 1Тема. Численное интегрирование функций
Решаемые задачи:
вычисление объемов тел;
вычисление площадей фигур;
вычисление длин кривых;
и
т.д.
Слайд 2Численное интегрирование функций
Подходы:
замена исходной функции f (x) (заданной таблично или аналитически)
интерполирующим полиномом P(x) с известной первообразной;
подбор оптимальных узлов интегрирования при аналитически заданной функции f (x);
вероятностные или статистические методы.
подбор оптимальных узлов интегрирования при аналитически заданной функции f (x);
вероятностные или статистические методы.
Слайд 3Вероятностные (статистические) методы
Пример: задан шар
Соотношение объёмов шара и куба, в который
вписан шар:
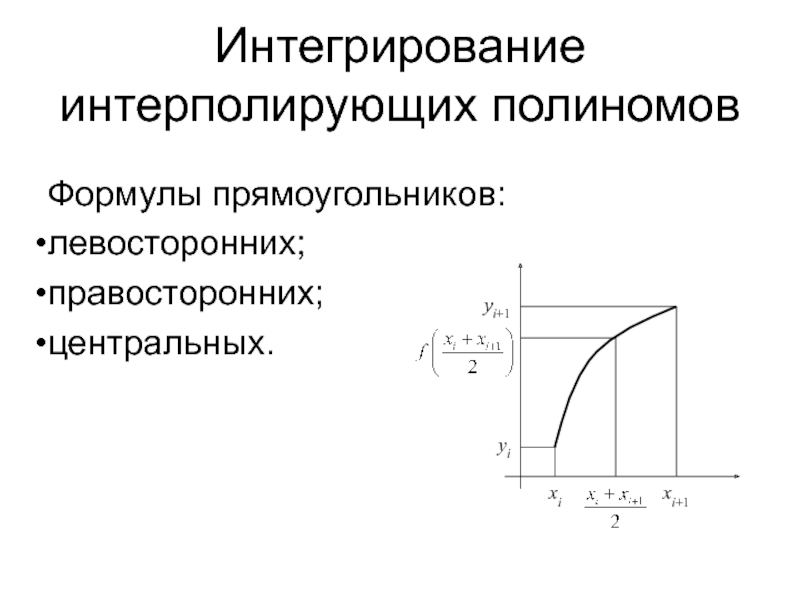
Слайд 8Интегрирование интерполирующих полиномов
Формулы прямоугольников:
левосторонних;
правосторонних;
центральных.
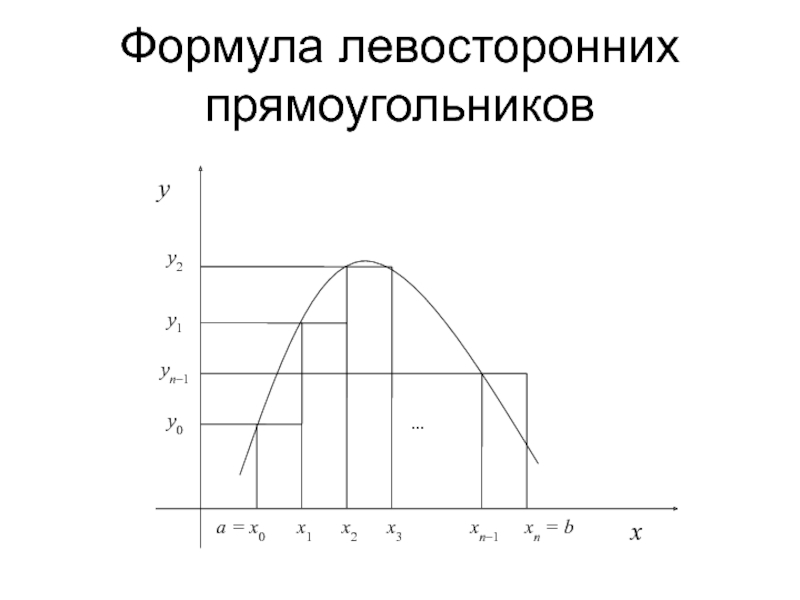
Слайд 9Формула левосторонних прямоугольников
На отрезке [xi, xi+1] полагаем p =1, Pi(x) =
yi. Получаем:
Для равномерной сетки
Для равномерной сетки
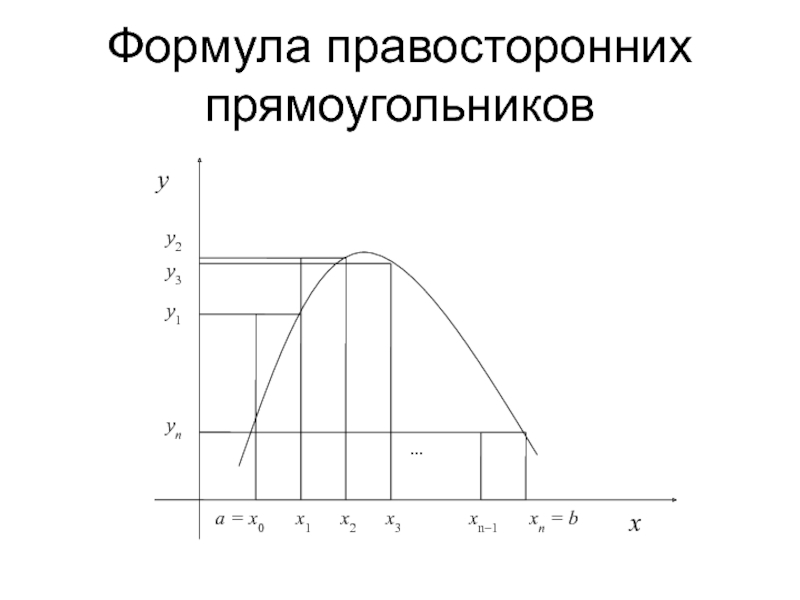
Слайд 11Формула правосторонних прямоугольников
На отрезке [xi, xi+1] полагаем p =1, Pi(x) =
yi+1. Получаем:
Для равномерной сетки
Для равномерной сетки
Слайд 18Квадратурные формулы
Если предположить, что cij = yip+j⋅Cij, то
где Aij – квадратурные
коэффициенты. Тогда
Слайд 27Квадратурные формулы
Если сетка равномерная, то
т.е. коэффициенты Aj не зависят от индекса
i. Для отрезка [a, b]
Слайд 30Коэффициенты Ньютона-Котеса
В случае равномерной сетки положим
Здесь Hi – коэффициенты Ньютона-Котеса. Т.е.
