- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Формулы приведения презентация
Содержание
- 1. Формулы приведения
- 2. Если под знаком преобразуемой тригонометрической функции содержится
- 3.
- 4.
- 5. Любая из формул приведения может быть записана
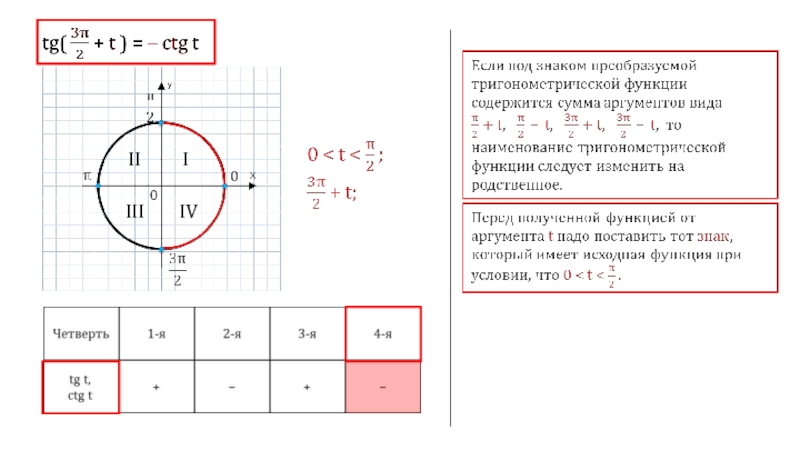
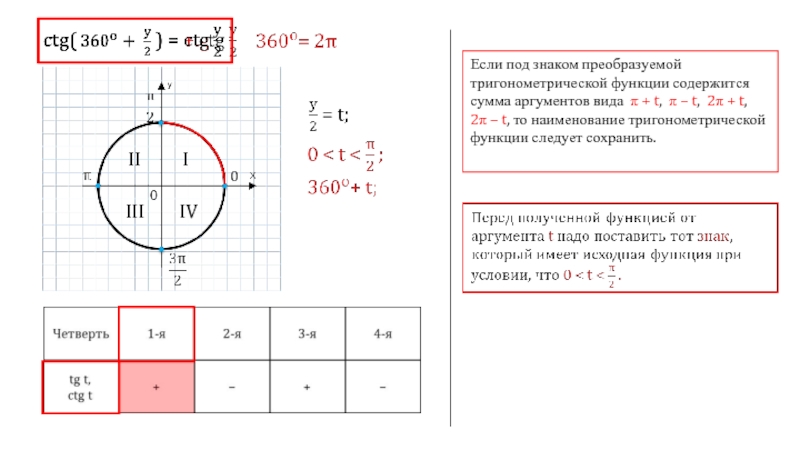
- 6. 0 I II III
- 7. 0 I II III
- 8. 0 I II III
- 9. 0 I II III
- 10. Пример 1. Вычислить с помощью формул приведения
- 11. Пример 1. Вычислить с помощью формул приведения
- 12. Доказательство. ⟹ меняем наименование
- 13. Доказательство. ⟹ наименование
- 14. Доказательство.
Если под знаком преобразуемой тригонометрической функции содержится сумма аргументов вида π + t, π – t, 2π + t, 2π – t, то наименование тригонометрической функции следует сохранить.
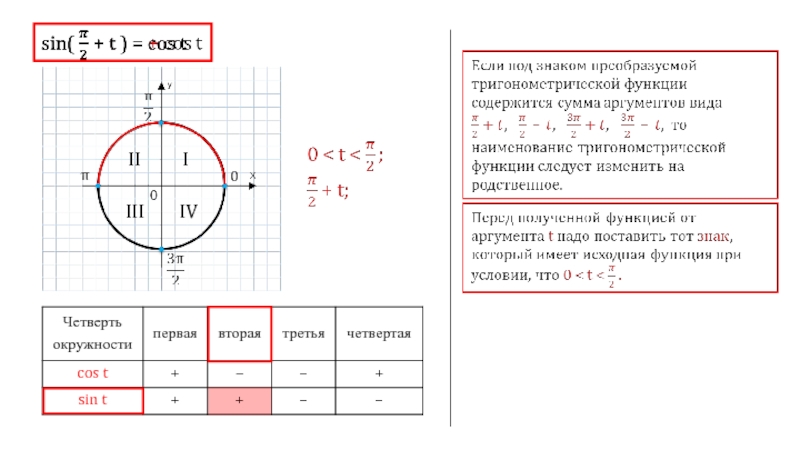
Слайд 2Если под знаком преобразуемой тригонометрической функции содержится сумма аргументов вида π
+ t, π – t, 2π + t, 2π – t, то наименование тригонометрической функции следует сохранить.
Слайд 5Любая из формул приведения может быть записана и для градусной меры
угла, то есть когда под знаком тригонометрической функции записано выражение вида
90° + α, 90° - α, 180° + α.
90° + α, 90° - α, 180° + α.
Слайд 6
0
I
II
III
IV
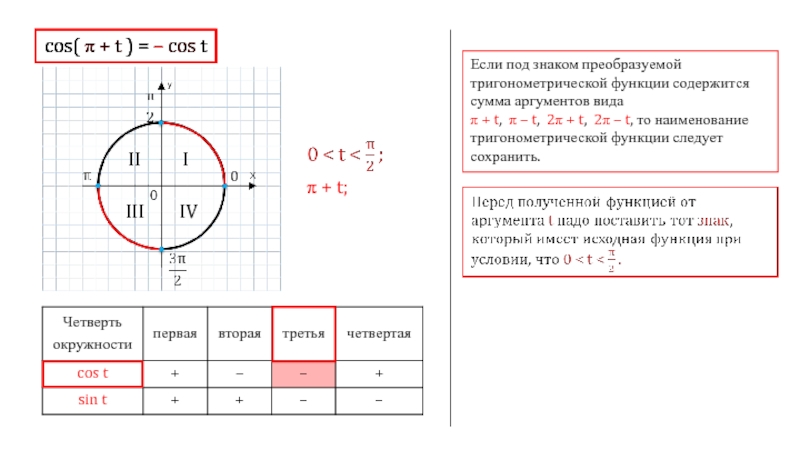
cos( π + t ) = – cos t
Если под знаком
преобразуемой тригонометрической функции содержится сумма аргументов вида
π + t, π – t, 2π + t, 2π – t, то наименование тригонометрической функции следует сохранить.
π + t, π – t, 2π + t, 2π – t, то наименование тригонометрической функции следует сохранить.
cos( π + t ) = – cos t
π + t;
cos( π + t ) = – cos t
Слайд 9
0
I
II
III
IV
Если под знаком преобразуемой тригонометрической функции содержится сумма аргументов вида π
+ t, π – t, 2π + t, 2π – t, то наименование тригонометрической функции следует сохранить.
Слайд 10Пример 1. Вычислить с помощью формул приведения sin ( –330° ).
Решение.
sin
( –t ) = – sin t
sin ( – 330°) = – sin 330°;
sin ( – 330°) = – sin 330° = – sin ( 360° – 30°);
⟹ наименование функции сохраним;
330° = 360° – 30° — аргумент IV четверти;
Слайд 11Пример 1. Вычислить с помощью формул приведения sin ( –330° ).
Решение.
sin
( –t ) = – sin t
sin ( – 330°) = – sin 330°;
sin ( – 330°) = – sin 330° = – sin ( 360° – 30°);
⟹ наименование функции сохраняем;
330° = 360° – 30° — аргумент IV четверти;
