- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Методы решения геометрических задач презентация
Содержание
- 1. Методы решения геометрических задач
- 2. Для решения сложных геометрических задач, следует научить
- 3. Опорные свойства: Теорема о вписанном угле и
- 4. Задача 1. В треугольнике KLM угол L
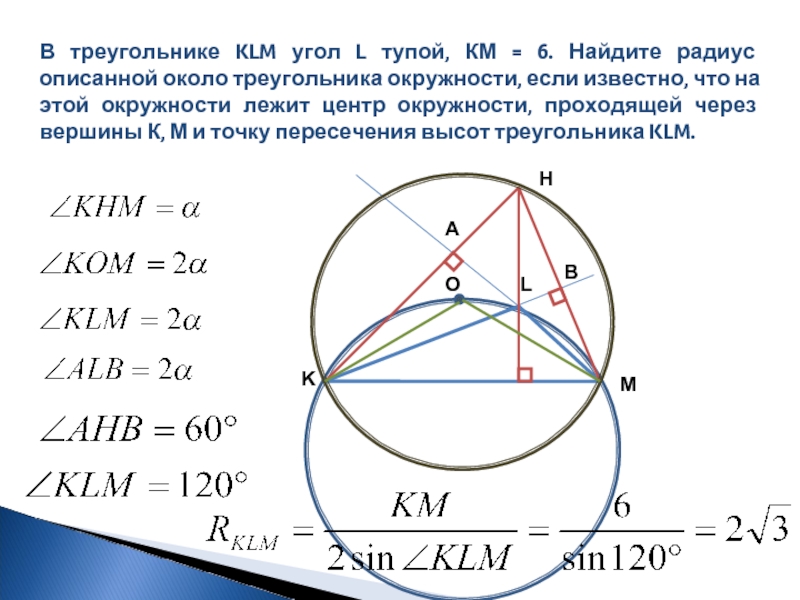
- 5. В треугольнике KLM угол L тупой, КМ
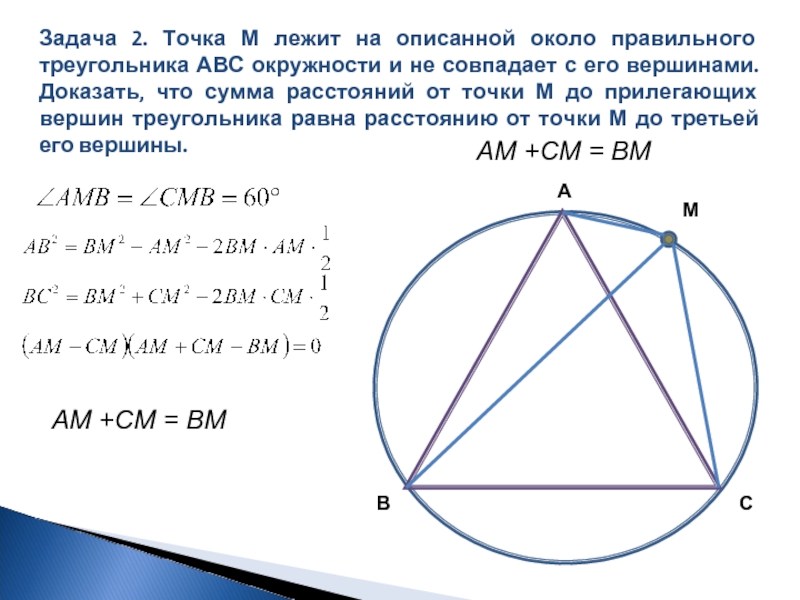
- 6. Задача 2. Точка М лежит на описанной
- 7. Задача 2. Точка М лежит на описанной
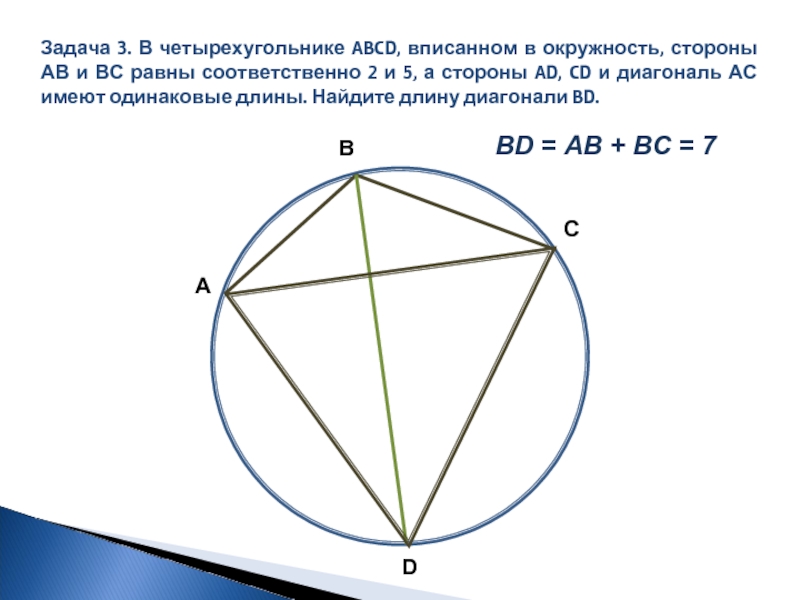
- 8. Задача 3. В четырехугольнике ABCD, вписанном в
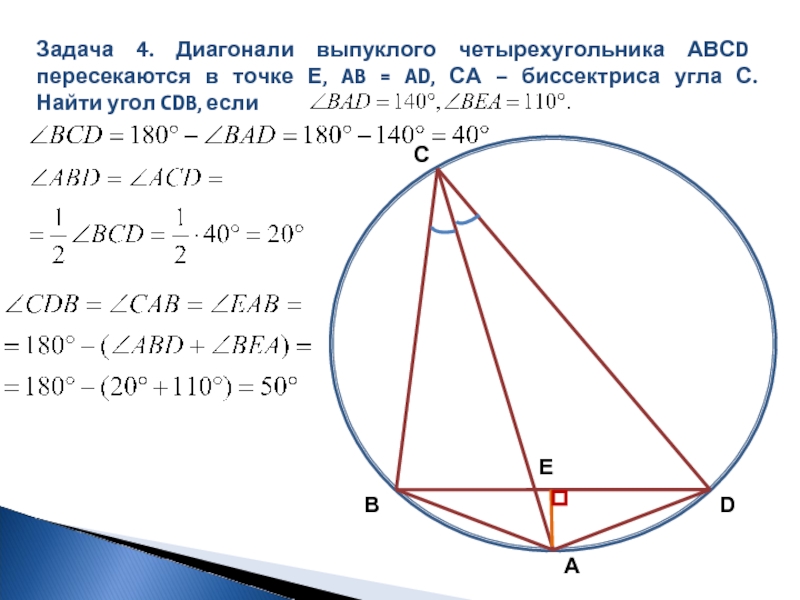
- 9. Задача 4. Диагонали выпуклого четырехугольника АВСD пересекаются
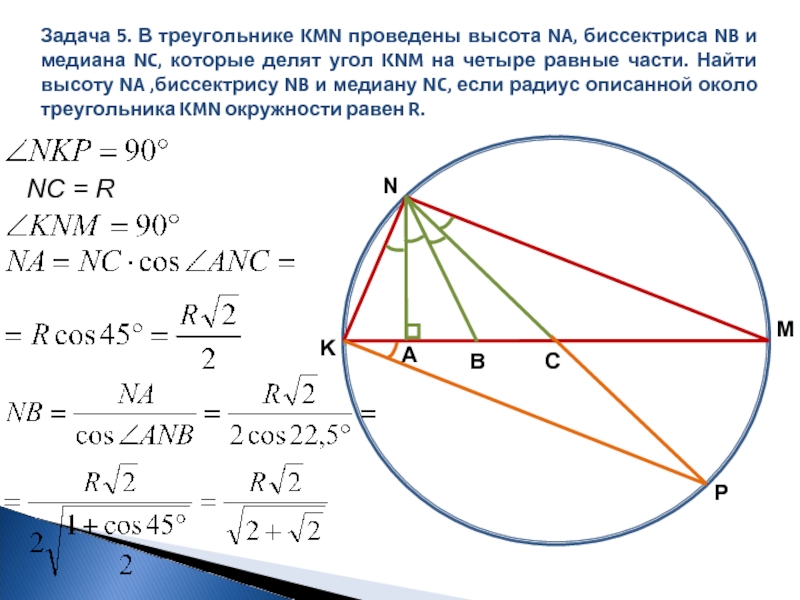
- 10. Задача 5. В треугольнике KMN проведены высота
- 11. Шарыгин И.Ф. Геометрия. Планиметрия. М.: Дрофа, 2001
Слайд 2Для решения сложных геометрических задач, следует научить учеников распознавать в них
Слайд 3Опорные свойства:
Теорема о вписанном угле и следствия
Теорема об угле между касательной
Теорема синусов
Вписанные и описанные многоугольники (свойства и признаки)
Точка на окружности
Слайд 4Задача 1. В треугольнике KLM угол L тупой, КМ = 6.
Слайд 5В треугольнике KLM угол L тупой, КМ = 6. Найдите радиус
H
O
A
B
Слайд 6Задача 2. Точка М лежит на описанной около правильного треугольника АВС
Слайд 7Задача 2. Точка М лежит на описанной около правильного треугольника АВС
А
В
С
М
АМ +СМ = ВМ
АМ +СМ = ВМ
Слайд 8Задача 3. В четырехугольнике ABCD, вписанном в окружность, стороны АВ и
А
В
С
D
BD = AB + ВС = 7
Слайд 9Задача 4. Диагонали выпуклого четырехугольника АВСD пересекаются в точке Е, AB
А
В
С
D
E
Слайд 10Задача 5. В треугольнике KMN проведены высота NA, биссектриса NB и
K
N
M
A
B
C
P
NC = R
Слайд 11Шарыгин И.Ф. Геометрия. Планиметрия. М.: Дрофа, 2001
Гордин Р.К. Геометрия. Планиметрия 7
Бутузов В.Ф., Кадомцев С.Б., Э.Г. Позняк, С.А. Шестаков, И.И. Юдина. Планиметрия. Пособие для углубленного изучения математики. М.: ФИЗМАТЛИТ, 2005
Алексеев В.Б., Панферов В.С., Тарасов В.А. Избранные задачи по геометрии. Окружность. М.: Илекса, 2012
Куланин Е.Д. Задачи по геометрии. М.: Илекса, 2012
Литература