- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Курс Эконометрика презентация
Содержание
- 1. Курс Эконометрика
- 2. Проверка статистических гипотез Темы занятий Парная регрессия Множественная регрессия Временные ряды Системы одновременных уравнений
- 3. Парная линейная регрессия Основная цель –
- 4. Для
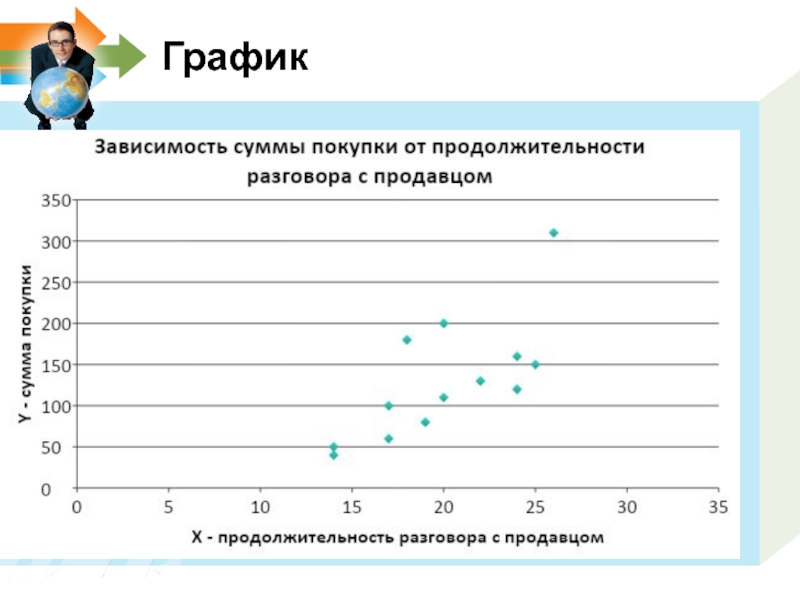
- 5. График
- 6. График линейной зависимости Y = a + b*X e13
- 7. Формулы для нахождения параметров При помощи
- 8. Коэффициент корреляции Показывает:
- 9. Шкала Чеддока для интерпретации коэффициента корреляции
- 10. Проверка качества подбора модели (вида уравнения) Коэффициент
- 11. Характеристики модели n
- 12. Проверка статистической значимости модели Fраспобр(α;1;n-2) Модель
- 13. Проверка статистической значимости параметров Н0:
- 14. Доверительный интервал для параметра параметр b с
- 15. Анализ данных Y = -133,5 +
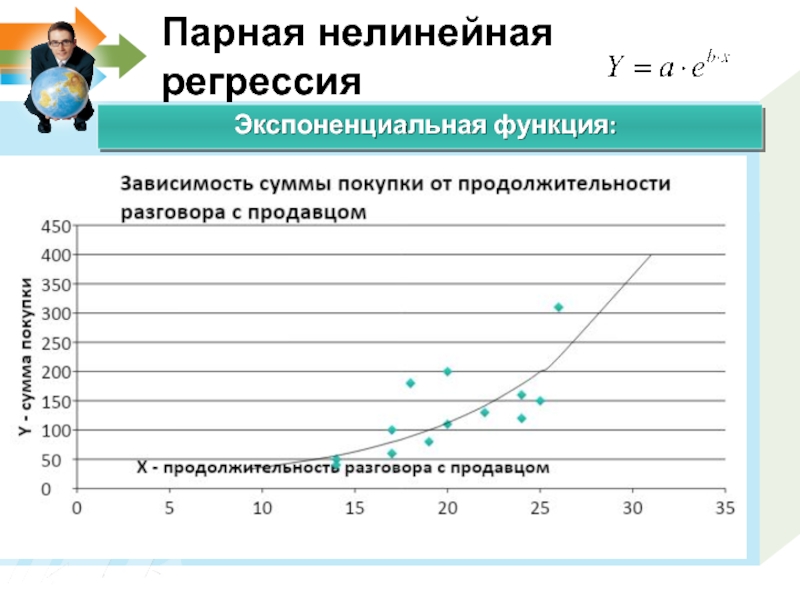
- 16. Парная нелинейная регрессия Экспоненциальная функция:
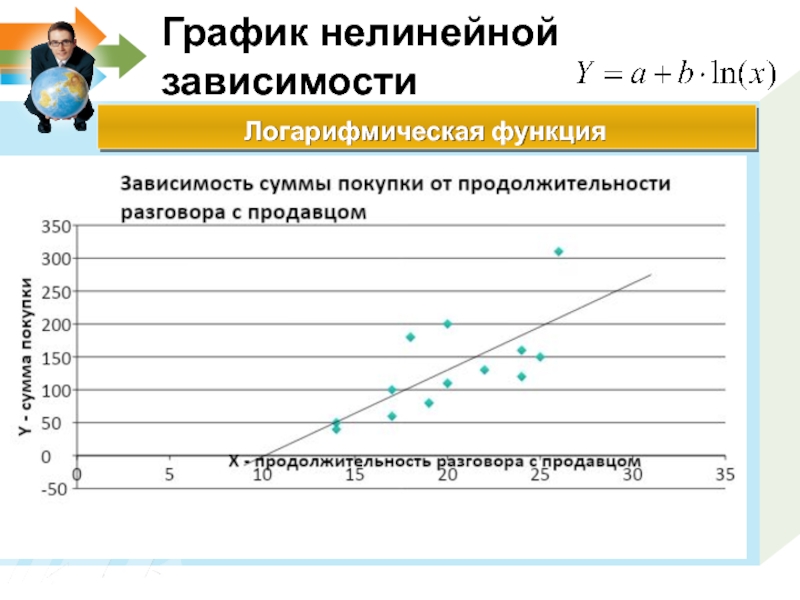
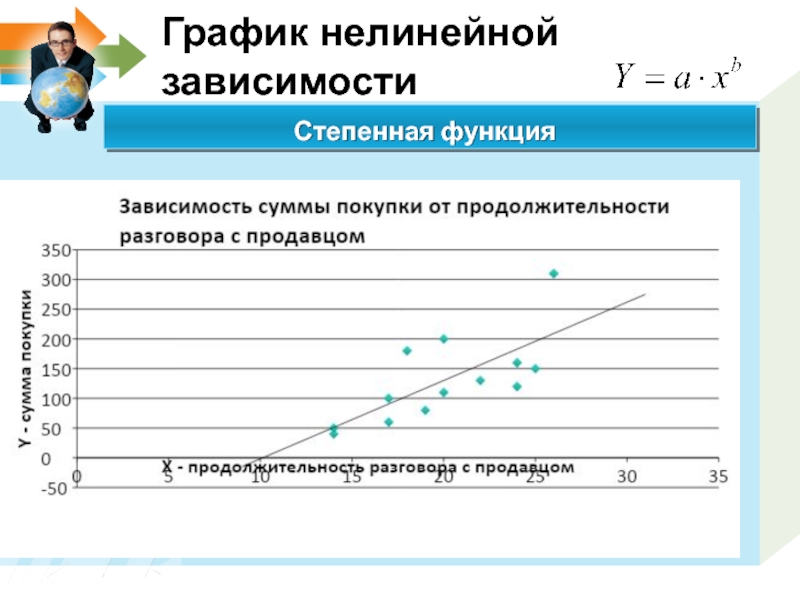
- 17. График нелинейной зависимости Логарифмическая функция
- 18. График нелинейной зависимости Describe a vision of company or strategic contents. Степенная функция
- 19. Эластичность Эластичность определяется по формуле:
- 20. Уравнение множественной регрессии Линейная модель:
- 21. Уравнение множественной регрессии в стандартизированном масштабе Уравнение
- 22. Проверка качества уравнения множественной регрессии Коэффициент детерминации: Скорректированный к-т детерминации:
- 23. Проверка статистической значимости модели Fраспобр(α;k;n-k-1) Модель
- 24. Спасибо за внимание! www.themegallery.com До свидания!
Слайд 2Проверка статистических гипотез
Темы занятий
Парная регрессия
Множественная регрессия
Временные ряды
Системы одновременных уравнений
Слайд 3Парная линейная регрессия
Основная цель – построить уравнение (модель) вида:
описывающее зависимость
a и b – называются параметрами модели.
Примеры зависимостей:
Выручки предприятия от расходов на рекламу;
Цены на нефть от курса доллара,
Количества баллов по эконометрике от количества часов, потраченных на её изучение и т.д.
Y = a + b*X
Слайд 4
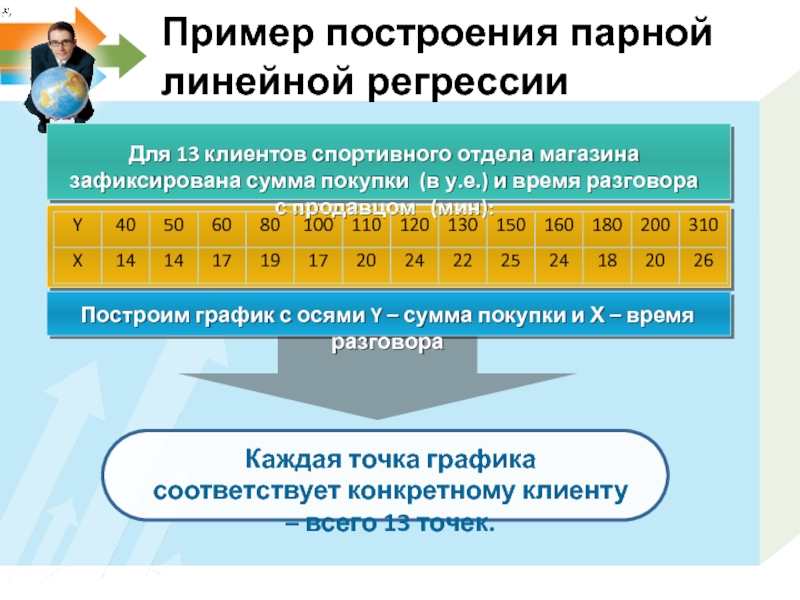
Для 13 клиентов спортивного отдела магазина зафиксирована сумма покупки (в у.е.)
Каждая точка графика соответствует конкретному клиенту – всего 13 точек.
Построим график с осями Y – сумма покупки и Х – время разговора
Пример построения парной линейной регрессии
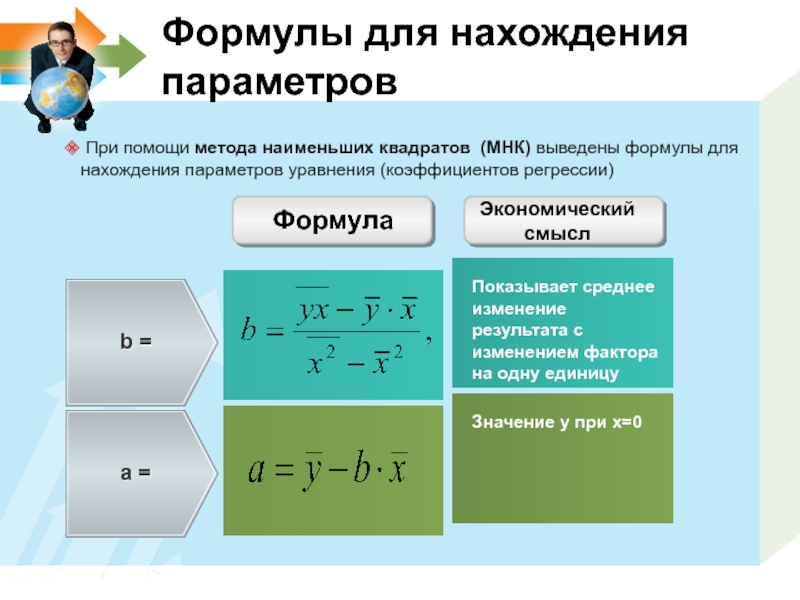
Слайд 7Формулы для нахождения параметров
При помощи метода наименьших квадратов (МНК) выведены
b =
a =
Значение y при x=0
Формула
Экономический смысл
Показывает среднее изменение результата с изменением фактора на одну единицу
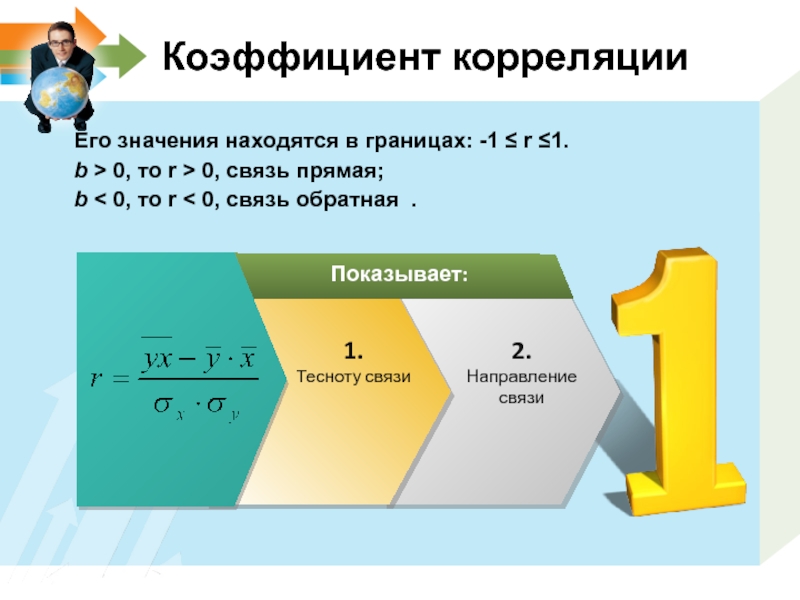
Слайд 8Коэффициент корреляции
Показывает:
2.
Направление связи
Его значения находятся в границах: -1 ≤ r ≤1.
b > 0, то r > 0, связь прямая;
b < 0, то r < 0, связь обратная .
1.
Тесноту связи
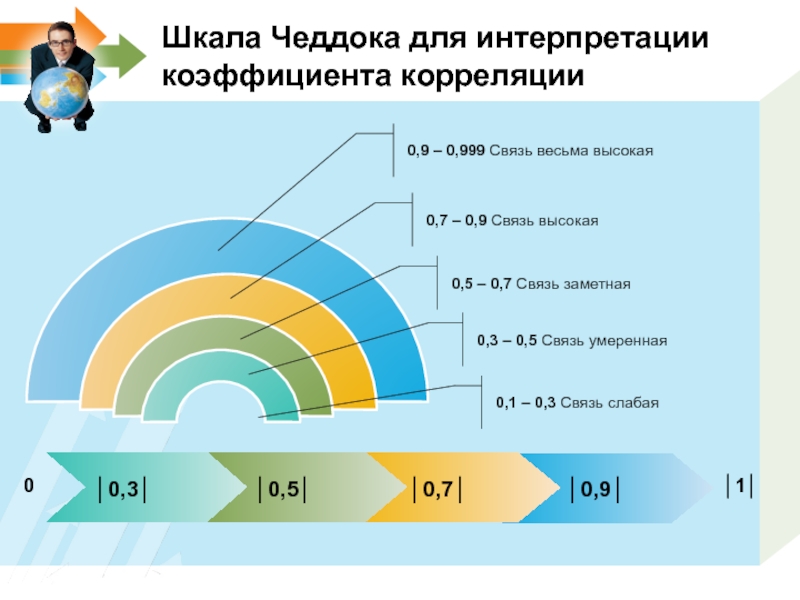
Слайд 9Шкала Чеддока для интерпретации коэффициента корреляции
0,1 – 0,3 Связь слабая
0,3 –
0,5 – 0,7 Связь заметная
0,7 – 0,9 Связь высокая
│0,3│
│0,5│
│0,7│
│0,9│
0,9 – 0,999 Связь весьма высокая
│1│
0
Слайд 10Проверка качества подбора модели (вида уравнения)
Коэффициент детерминации - характеризует долю дисперсии
δ^2 факторная
δ^2 общая
δ^2 остаточная
Слайд 11
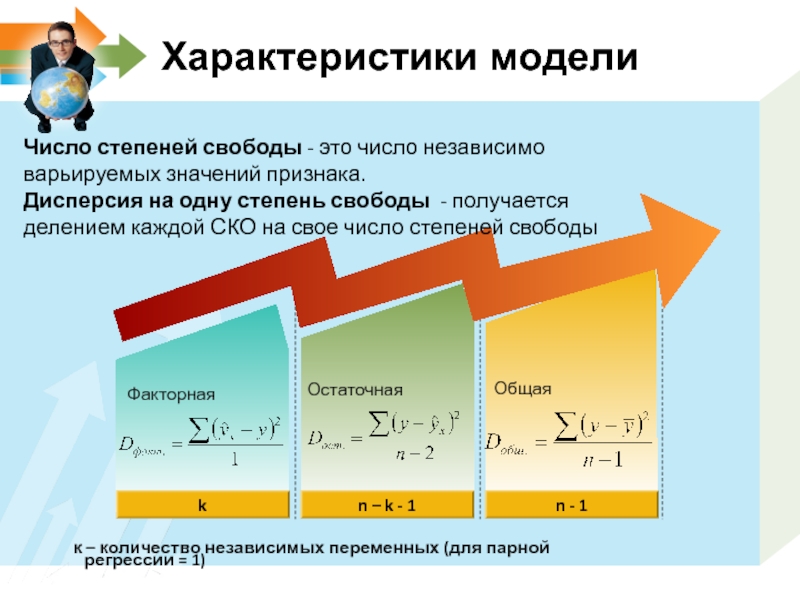
Характеристики модели
n - 1
Факторная
n – k - 1
k
Остаточная
Общая
Число степеней свободы
Дисперсия на одну степень свободы - получается делением каждой СКО на свое число степеней свободы
к – количество независимых переменных (для парной регрессии = 1)
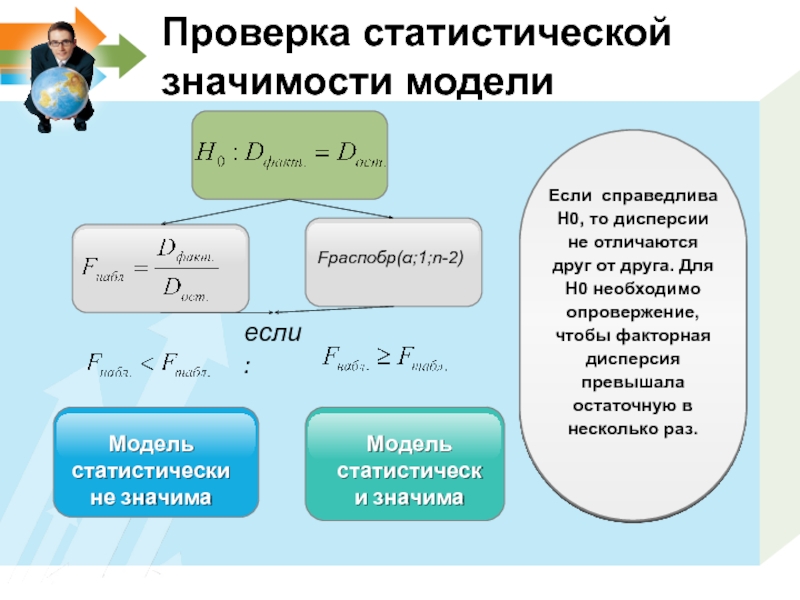
Слайд 12Проверка статистической значимости модели
Fраспобр(α;1;n-2)
Модель статистически не значима
Модель статистически значима
если:
Если справедлива
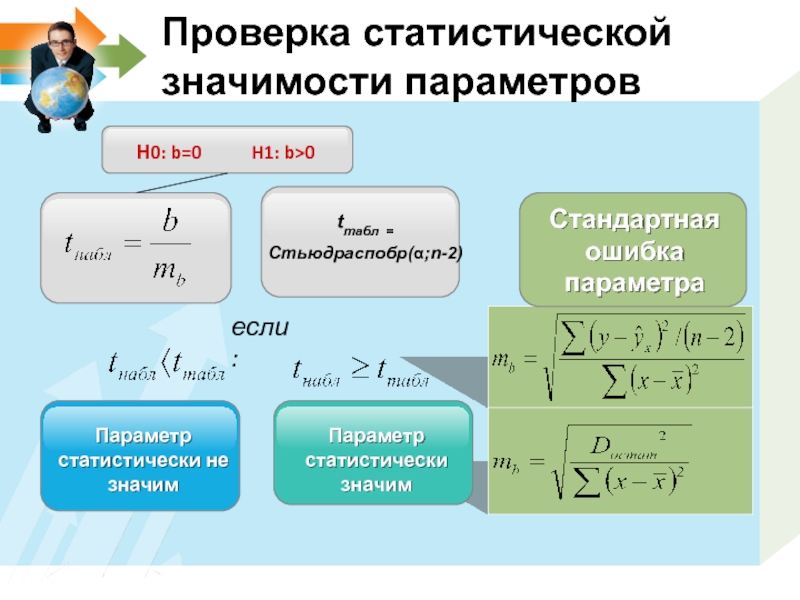
Слайд 13Проверка статистической значимости параметров
Н0: b=0 H1:
tтабл =
Стьюдраспобр(α;n-2)
Стандартная ошибка параметра
Параметр статистически не значим
Параметр статистически значим
если:
Слайд 14Доверительный интервал для параметра
параметр b с надежностью α лежит в интервале:
надежность
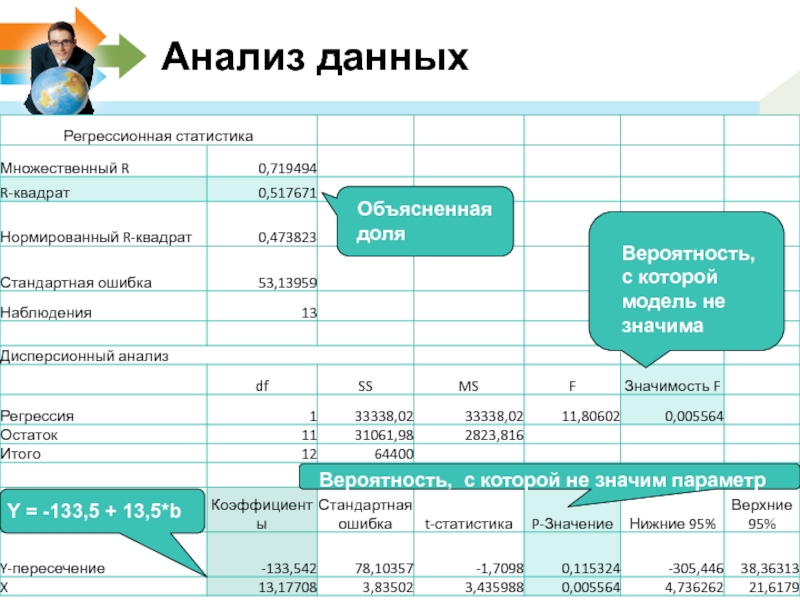
Слайд 15Анализ данных
Y = -133,5 + 13,5*b
Вероятность, с которой модель не значима
Вероятность,
Объясненная доля
Слайд 18График нелинейной зависимости
Describe a vision of company or strategic contents.
Степенная функция
Слайд 20Уравнение множественной регрессии
Линейная модель:
На любой экономический показатель чаще всего оказывает влияние
Например, спрос на некоторое благо определяется не только ценой данного блага, но и ценами на замещающие и дополняющие блага, доходом потребителей и многими другими факторами.
Слайд 21Уравнение множественной регрессии в стандартизированном масштабе
Уравнение регрессии в стандартизованном масштабе имеет
стандартизированные параметры:
Система уравнений:
Слайд 22Проверка качества уравнения множественной регрессии
Коэффициент детерминации:
Скорректированный к-т детерминации:
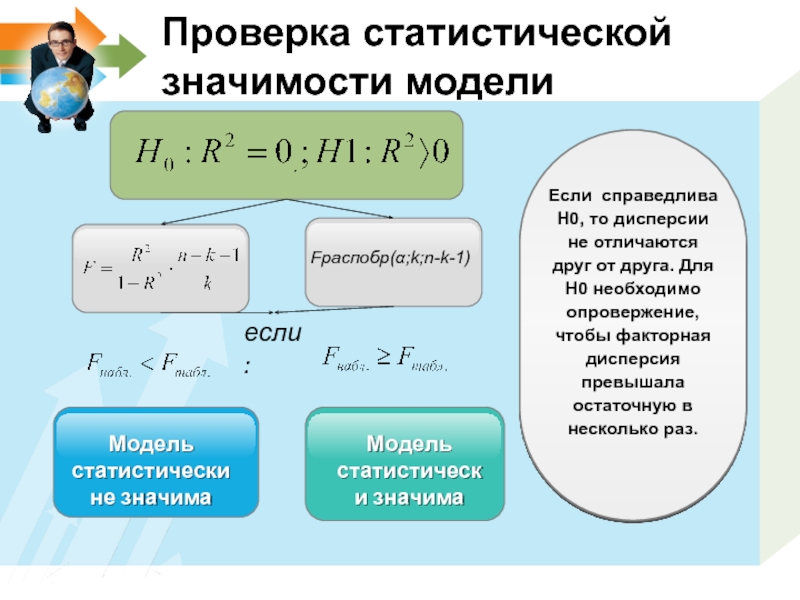
Слайд 23Проверка статистической значимости модели
Fраспобр(α;k;n-k-1)
Модель статистически не значима
Модель статистически значима
если:
Если справедлива