- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Кривые второго порядка на плоскости презентация
Содержание
- 1. Кривые второго порядка на плоскости
- 2. Лекция 8. Кривые второго порядка на плоскости
- 3. где не все коэффициенты А, В,
- 4. Вырожденные кривые второго порядка : 1. пустое
- 5. Всякое уравнение (1), задающее невырожденную
- 6. Эллипсом называется кривая второго порядка с каноническим уравнением
- 7. достроив затем остальные части путём
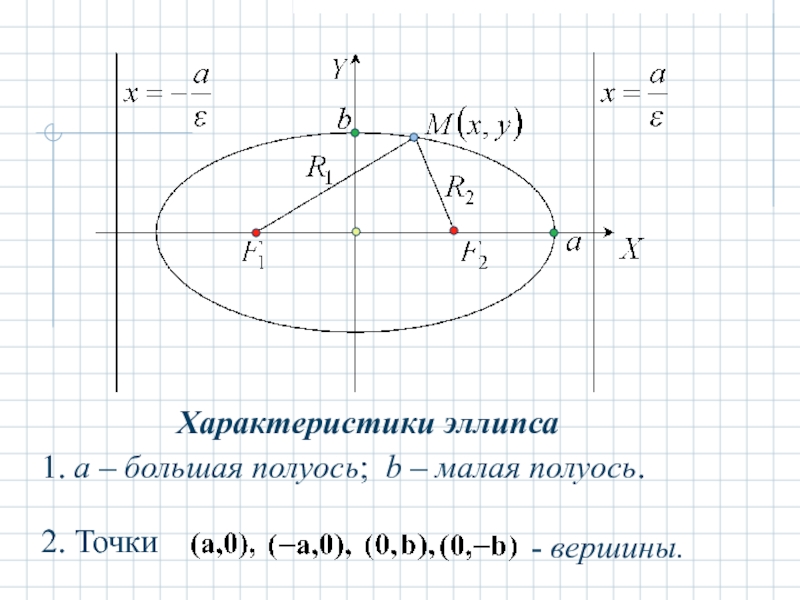
- 8. Характеристики эллипса 1. a – большая полуось; b – малая полуось. - вершины.
- 9. - центр. - фокусы, где фокальные
- 10. директрисы эллипса. Замечание. уравнение
- 11. Вывод. Замечание.
- 12. Гиперболой называется кривая второго порядка с каноническим уравнением
- 14. Характеристики гиперболы 1. a – действительная
- 15. директрисы гиперболы. основной прямоугольник.
- 16. Вывод. Замечание. Последнее высказывание можно
- 17. Алгоритм построения чертежа гиперболы. 1. Построение
- 18. Параболой называется кривая второго порядка с каноническим
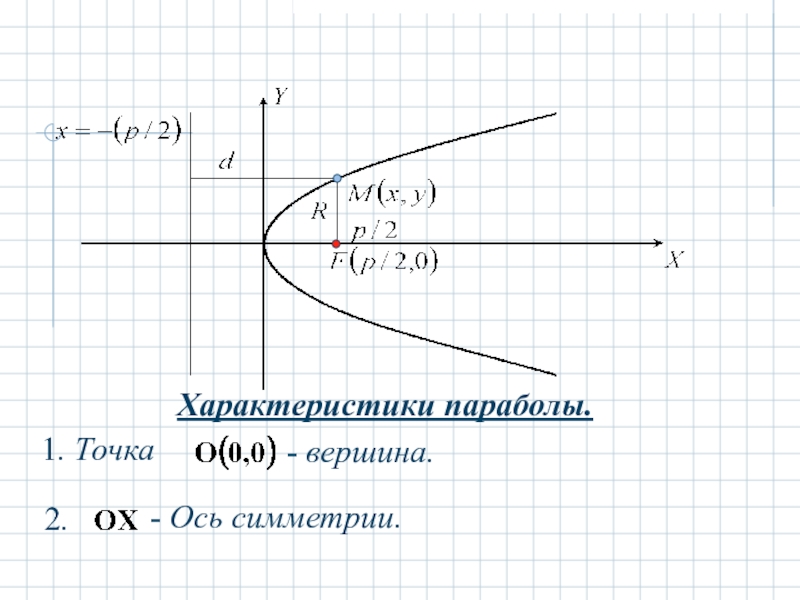
- 19. Характеристики параболы. - вершина. - Ось симметрии.
- 20. - фокус. фокальный радиус точки параболы. директриса.
- 21. Вывод. Замечание. Последнее высказывание можно
- 22. Канонические уравнения кривых второго порядка со смещенным центром (вершиной).
- 23. Выполним замену Геометрически:
- 24. Пример. Тип кривой – гипербола со
- 25. Два признака неканоничности: Устранение признаков неканоничности: Геометрически:
- 26. Геометрически:
Лекция 8. Кривые второго порядка на плоскости I. Основные понятия. 2. Исследование формы кривых второго порядка по их каноническим уравнениям.
Слайд 2Лекция 8.
Кривые второго порядка на плоскости
I. Основные понятия.
2. Исследование формы кривых второго
порядка по их каноническим уравнениям.
порядка по их каноническим уравнениям.
3. Приведение уравнений кривых второго порядка к каноническому виду.
Слайд 3 где не все коэффициенты А, В, С равны нулю.
Алгебраической кривой второго порядка
называется кривая , уравнение которой в декартовой
системе координат имеет вид:
называется кривая , уравнение которой в декартовой
системе координат имеет вид:
Слайд 5 Всякое уравнение (1), задающее невырожденную
кривую, путём преобразования координат
можно
привести к каноническому виду (одному из трех):
привести к каноническому виду (одному из трех):
Слайд 7
достроив затем остальные части путём зеркального
отражения найденных фрагментов кривой
относительно координатных осей.
Рассмотрим уравнение эллипса в первой четверти.
Слайд 10директрисы эллипса.
Замечание.
уравнение окружности радиуса R с центром в начале
координат О(0,0).
Вычислим
Слайд 11
Вывод.
Замечание.
Последнее высказывание можно использовать как
определение эллипса. Тогда, используя рисунок,
можно получить каноническое уравнение эллипса.
можно получить каноническое уравнение эллипса.
Слайд 14 Характеристики гиперболы
1. a – действительная полуось; b – мнимая полуось.
- вершины.
- центр.
- фокусы, где
- фокальные расстояния точки М
гиперболы.
эксцентриситет гиперболы.
Слайд 15директрисы гиперболы.
основной прямоугольник.
– асимптоты гиперболы (диагонали основного прямоугольника).
Вычислим
Слайд 16Вывод.
Замечание.
Последнее высказывание можно использовать как
определение гиперболы. Тогда, используя
рисунок,
можно получить её каноническое уравнение.
можно получить её каноническое уравнение.
Слайд 17Алгоритм построения чертежа гиперболы.
1. Построение основного прямоугольника.
2. Построение асимптот
– диагоналей.
3. Определение вершин гиперболы (выяснение
вопроса о том, какую координатную ось гипербола
пересекает).
4. Построение гиперболы.
Слайд 18Параболой называется кривая второго порядка с
каноническим уравнением
Рассмотрим уравнение параболы
в первой четверти.
Слайд 21Вывод.
Замечание.
Последнее высказывание можно использовать как
определение параболы. Тогда, используя
рисунок,
можно получить её каноническое уравнение.
можно получить её каноническое уравнение.
Слайд 24Пример.
Тип кривой – гипербола со смещенным в точку (-1,1)
центром.
b=2 - действительная полуось, a=3 - мнимая
полуось.
полуось.
