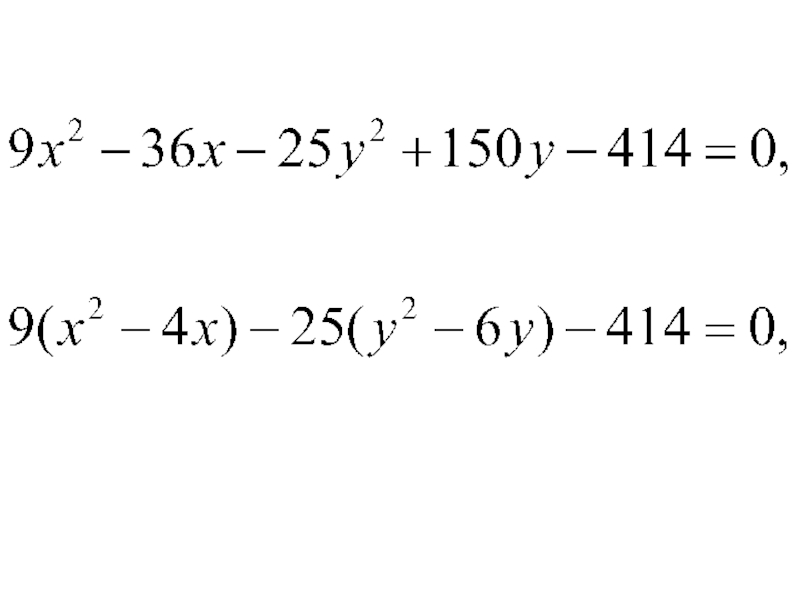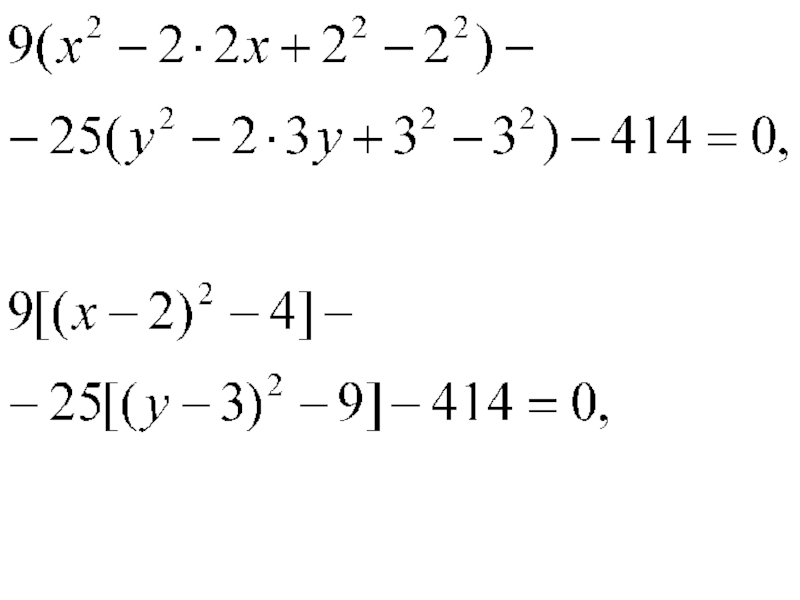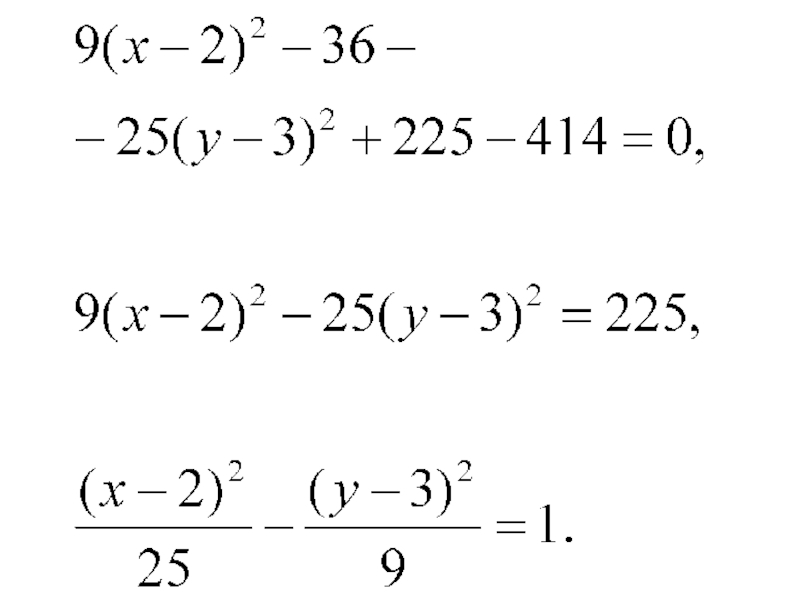- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Кривые второго порядка презентация
Содержание
- 1. Кривые второго порядка
- 2. где коэффициенты А,В,С одновременно не обращаются
- 3. Окружностью называется множество точек плоскости, равноудаленных от
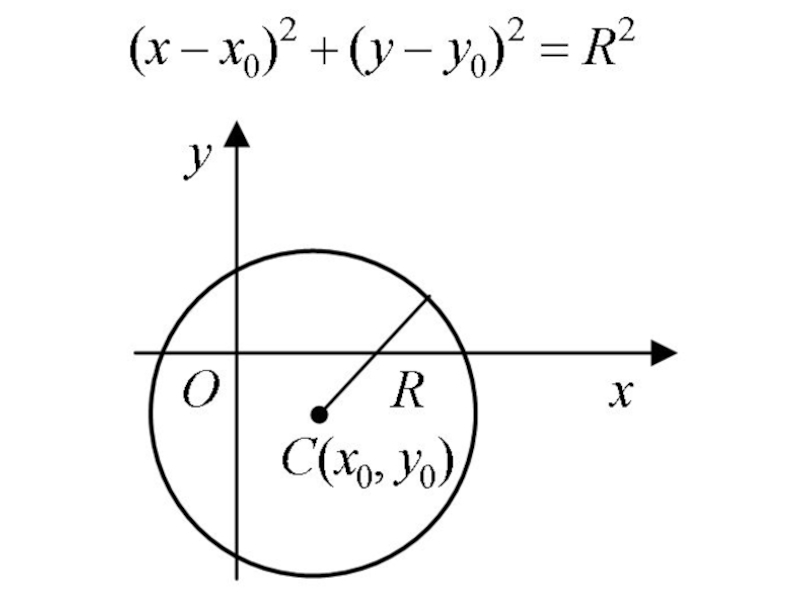
- 4. Если центр окружности находится в точке C(x0,
- 6. Пусть на плоскости заданы две точки F1
- 7. Эллипсом называется множество точек плоскости, сумма расстояний
- 9. Если систему координат выбрать так, как указано
- 10. Фокусы эллипса расположены в точках F1(-c; 0)
- 11. Пусть на плоскости заданы две точки F1
- 12. Гиперболой называется множество точек плоскости, модуль разности
- 14. Если систему координат выбрать так, как указано
- 15. Гипербола состоит из двух ветвей и расположена
- 16. При построении гиперболы вначале строят основной прямоугольник
- 17. Вершины гиперболы расположены в точках с координатами
- 18. Уравнение
- 19. Пусть на плоскости задана точка F и
- 21. Если систему координат выбрать так, как указано
- 22. Эта парабола симметрична относительно оси Ох. Директрисой
- 23. Если p < 0, то парабола направлена
- 24. Для того, чтобы построить кривую второго порядка,
- 25. Пример. Определить тип линии и схематически построить её:
- 26. Решение. Приведем заданное уравнение к каноническому виду.
- 30. Совершим параллельный перенос координатных осей по формулам:
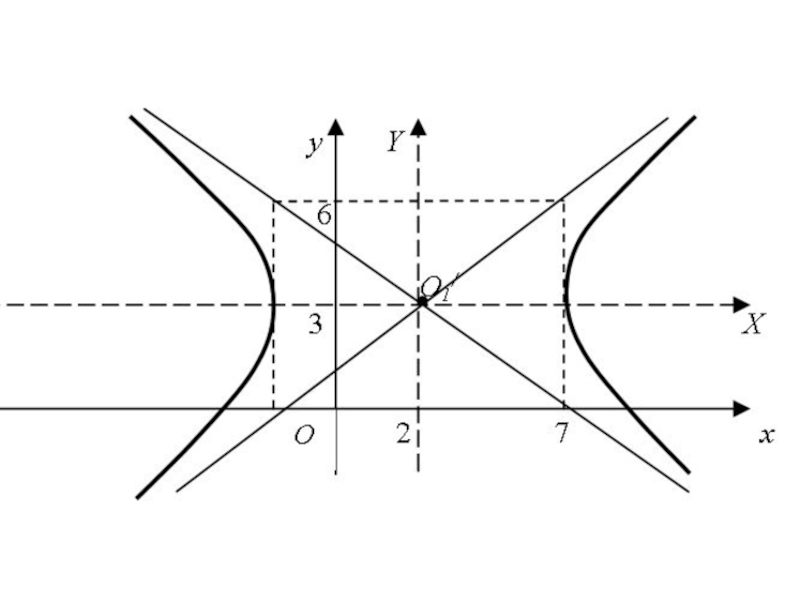
- 31. Получили каноническое уравнение гиперболы (действительная полуось а = 5, мнимая полуось b =3)
где коэффициенты А,В,С одновременно не обращаются в нуль. При А = В = С = 0 уравнение задаёт прямую, которая называется линией первого порядка. К числу линий второго порядка относятся
Слайд 1Кривые второго порядка
Кривой второго порядка называется линия, уравнение которой в
декартовой системе координат имеет вид
Слайд 2 где коэффициенты А,В,С одновременно не обращаются в нуль. При А
= В = С = 0 уравнение задаёт прямую, которая называется линией первого порядка.
К числу линий второго порядка относятся окружность, эллипс, гипербола и парабола.
К числу линий второго порядка относятся окружность, эллипс, гипербола и парабола.
Слайд 3Окружностью называется множество точек плоскости, равноудаленных от данной точки (центра).
Если центр
окружности поместить в начало координат, то каноническое уравнение окружности радиусом R имеет вид
Слайд 6Пусть на плоскости заданы две точки F1 и F2, расстояние между
которыми равно 2с, и задано число a > c.
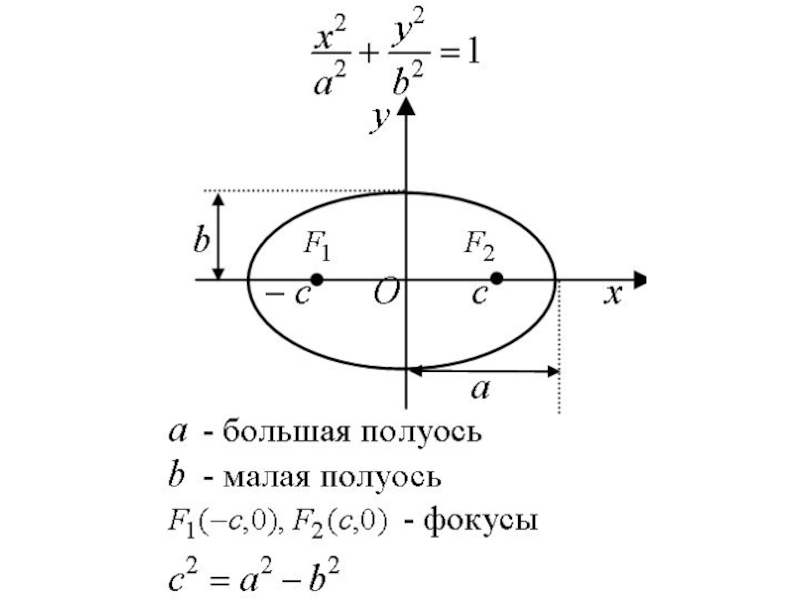
Слайд 7Эллипсом называется множество точек плоскости, сумма расстояний от которых до двух
данных точек F1 и F2 (фокусов) есть величина постоянная, равная 2а.
Слайд 9Если систему координат выбрать так, как указано на рис., то каноническое
уравнение эллипса запишется в виде
где а – большая, b – малая полуоси эллипса (при a>b).
где а – большая, b – малая полуоси эллипса (при a>b).
Слайд 10Фокусы эллипса расположены в точках F1(-c; 0) и F2(c; 0).
Окружность
есть частный случай эллипса при a = b.
Слайд 11Пусть на плоскости заданы две точки F1 и F2, расстояние между
которыми равно 2с, и задано число a < c.
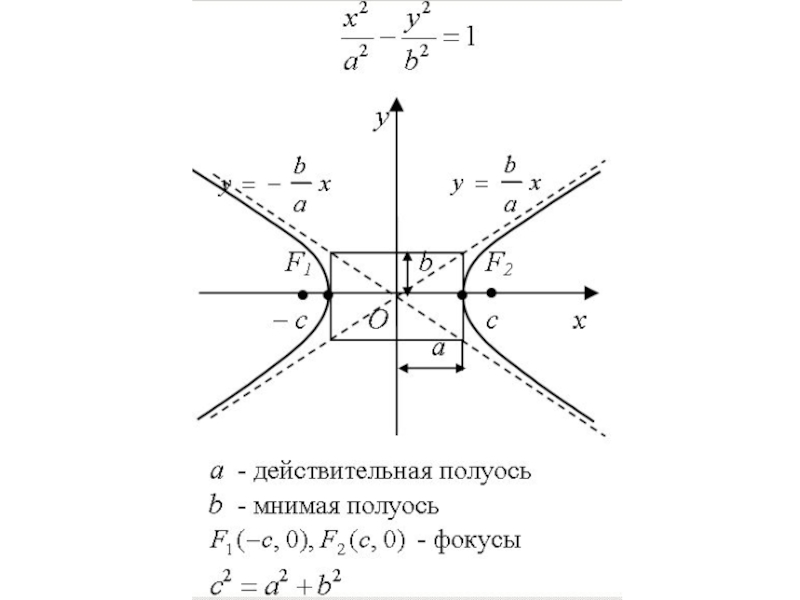
Слайд 12Гиперболой называется множество точек плоскости, модуль разности расстояний от которых до
двух данных точек F1 и F2 (фокусов) есть величина постоянная, равная 2а.
Слайд 14Если систему координат выбрать так, как указано на рис., то каноническое
уравнение гиперболы запишется в виде
где
а – действительная, b – мнимая полуоси гиперболы.
где
а – действительная, b – мнимая полуоси гиперболы.
Слайд 15Гипербола состоит из двух ветвей и расположена симметрично относительно координатных осей.
При этом ее ветви при удалении в бесконечность как угодно близко подходят к прямым которые называются асимптотами гиперболы.
Слайд 16При построении гиперболы вначале строят основной прямоугольник со сторонами x =
± a, y = ± b. Затем через противоположные вершины этого прямоугольника проводят прямые, которые являются асимптотами гиперболы.
Слайд 17Вершины гиперболы расположены в точках с координатами (– а,0) и (а,0),
а фокусы – в точках F1(-c; 0) и F2(c; 0).
Слайд 18Уравнение
(или ) также задаёт гиперболу, сопряженную с гиперболой
Действительная и мнимая полуоси этой гиперболы соответственно равны b и а.
Действительная и мнимая полуоси этой гиперболы соответственно равны b и а.
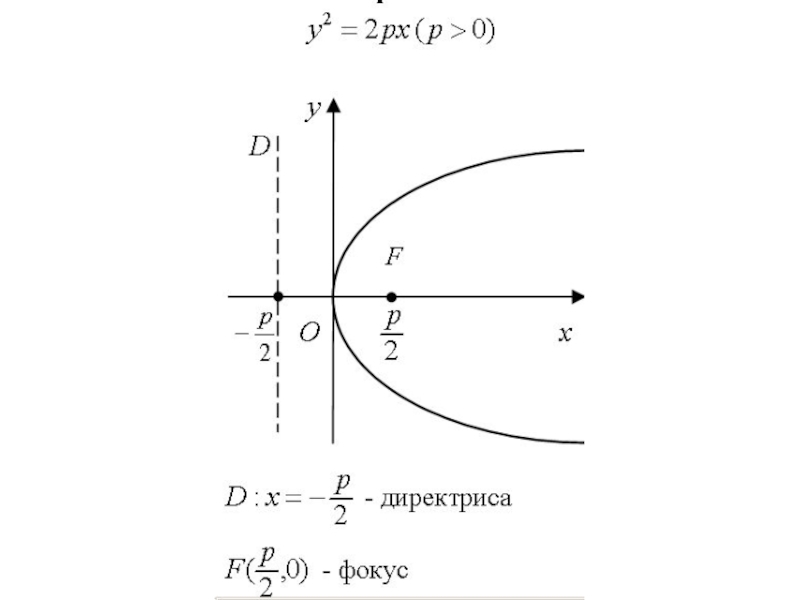
Слайд 19Пусть на плоскости задана точка F и прямая D, расстояние между
которыми равно р.
Параболой называется множество точек плоскости, равноудаленных от данной точки F (фокуса) и данной прямой D (директрисы).
Параболой называется множество точек плоскости, равноудаленных от данной точки F (фокуса) и данной прямой D (директрисы).
Слайд 21Если систему координат выбрать так, как указано на рис., то каноническое
уравнение параболы запишется в виде
Слайд 22Эта парабола симметрична относительно оси Ох. Директрисой является прямая
точка
– фокус параболы, р – параметр параболы.
Слайд 23Если p < 0, то парабола направлена в противоположную сторону.
Уравнение
задаёт параболу, симметричную относительно оси Оу.
Слайд 24Для того, чтобы построить кривую второго порядка, заданную общим уравнением, уравнение
кривой приводят к каноническому виду и переходят к новой системе координат.
Слайд 26Решение. Приведем заданное уравнение к каноническому виду. Для этого в исходном
уравнении выделим полные квадраты по переменным х и у. Перепишем исходное уравнение в виде:
Слайд 30Совершим параллельный перенос координатных осей по формулам:
(2,
3) – координаты центра O1 системы координат X и Y. В этой системе координат уравнение принимает вид:
Слайд 31Получили каноническое уравнение гиперболы (действительная полуось а = 5, мнимая полуось
b =3)
