- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Ковариация и собственный вектор презентация
Содержание
- 1. Ковариация и собственный вектор
- 2. Временной ряд рассматривается либо как
- 3. Показатели центра распределения
- 4. Показатели вариации Дисперсия
- 5. Показатели вариации Среднеквадратическое
- 6. Показатели вариации Ковариация
- 7. Показатели вариации Коэффициент
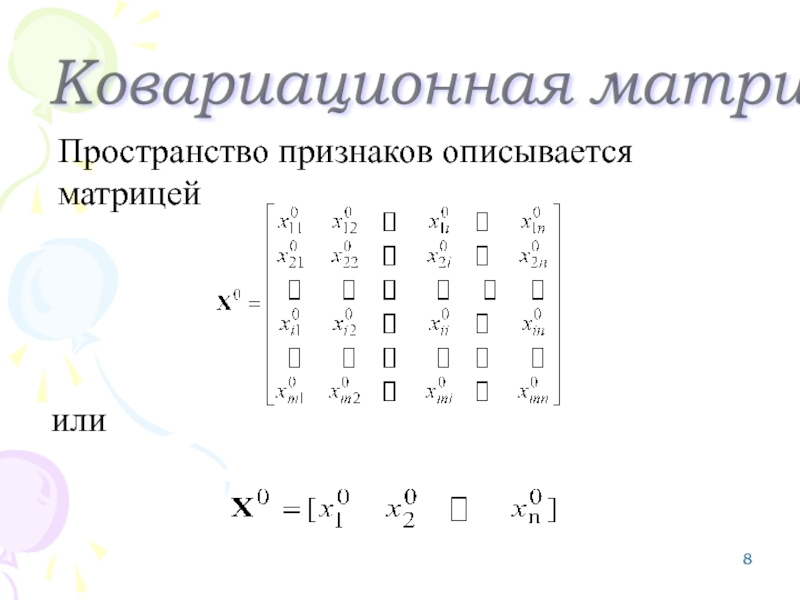
- 8. Ковариационная матрица
- 9. Операции с данными
- 10. Ковариационная матрица
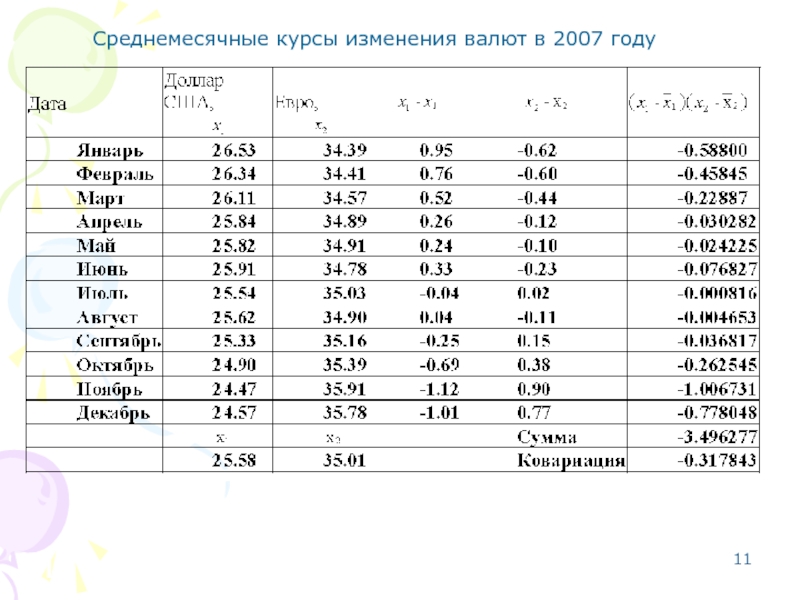
- 11. Среднемесячные курсы изменения валют в 2007 году
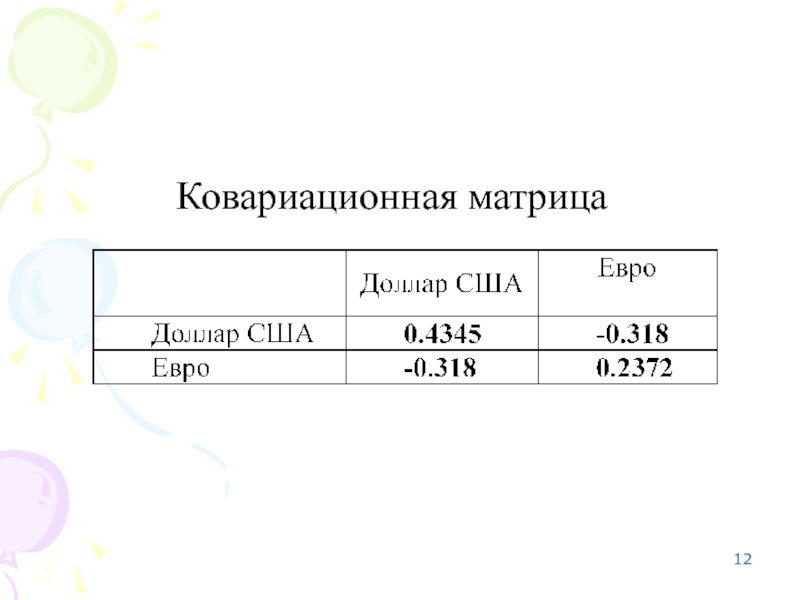
- 12. Ковариационная матрица
- 13. Вычисление корреляционной матрицы
- 14. Матрица вторых моментов Вычисление вторых моментов
- 15. Матрица нормированных вторых моментов
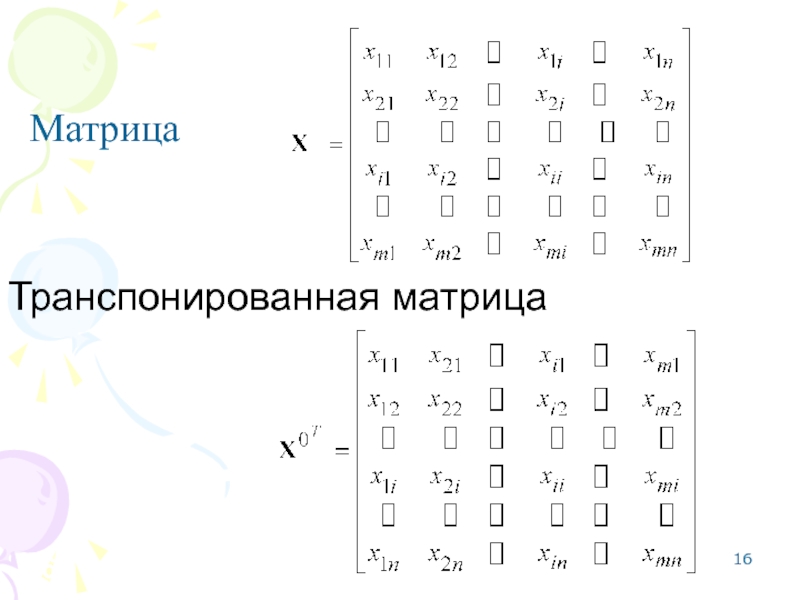
- 16. Транспонированная матрица Матрица
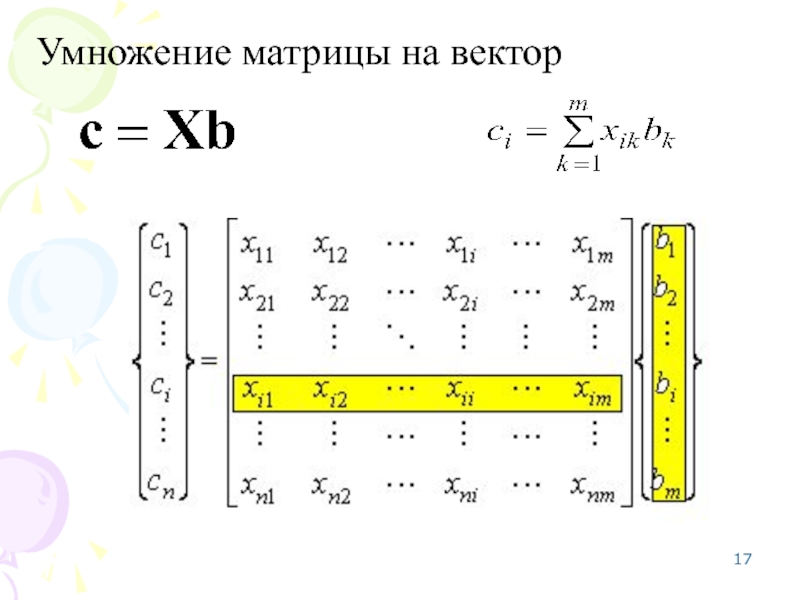
- 17. Умножение матрицы на вектор
- 18. Пример вектора и собственного вектора
- 19. Уравнение собственных векторов Собственный вектор
- 20. Алгоритм вычисления
- 21. Алгоритм вычисления
- 22. Свойства собственных векторов. Матрица n x
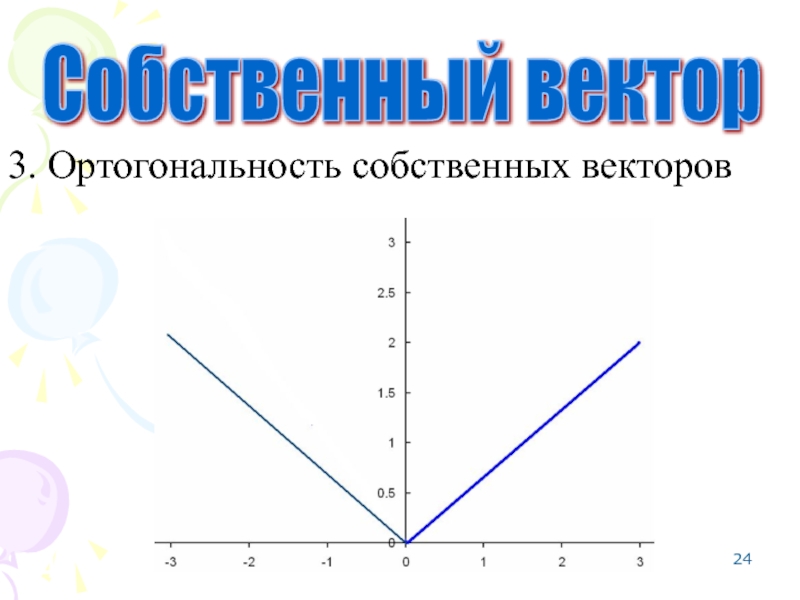
- 23. 3. Ортогональность собственных векторов
- 24. 3. Ортогональность собственных векторов Собственный вектор
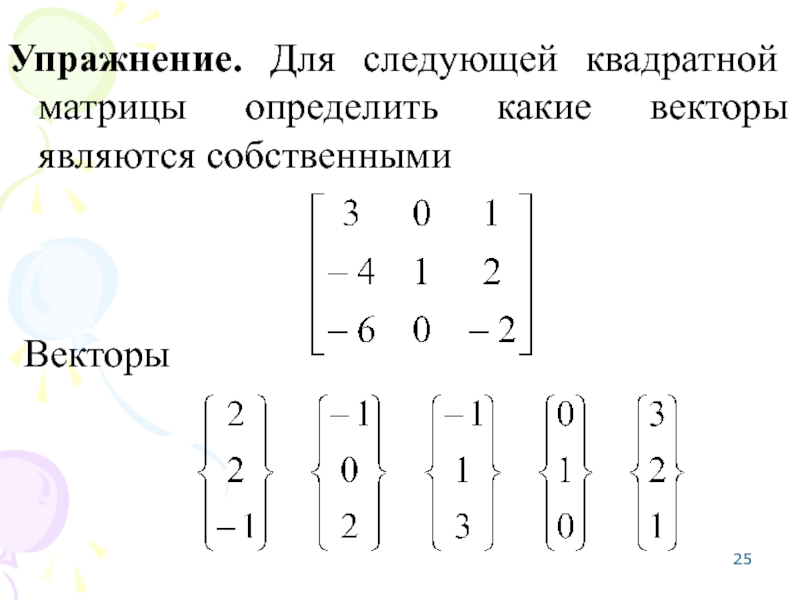
- 25. Упражнение. Для следующей квадратной матрицы определить какие
Временной ряд рассматривается либо как некоторая выборка из генеральной совокупности либо как описание некоторой детерминированной функции. Все значения каждого признака в различные моменты времени образуют временной ряд, который
Слайд 2
Временной ряд рассматривается либо как некоторая выборка из генеральной совокупности либо
как описание некоторой детерминированной функции.
Все значения каждого признака в различные моменты времени образуют временной ряд, который обозначается вектором
Все значения каждого признака в различные моменты времени образуют временной ряд, который обозначается вектором
1. Подготовка данных
Слайд 3
Показатели центра распределения
Среднеарифметические значения временных рядов:
Мода — это наиболее
часто наблюдаемая величина изучаемого временного ряда
Медиана — это значение наблюдения, которое находится в середине ранжированного ряда данных, т.е. наблюдение, занимающее срединное положение
Слайд 4
Показатели вариации
Дисперсия – отклонение наблюдаемого значения (для каждого наблюдения) от
среднего арифметического (несмещенная оценка) :
Если размер выборки относительно ограничен, то для более точного расчета применяется формула смещенной (исправленной) дисперсии:
Слайд 5
Показатели вариации
Среднеквадратическое (стандартное) отклонение показывает абсолютное отклонение измеренных значений от
среднего арифметического и определяется по формуле :
Слайд 6
Показатели вариации
Ковариация двух случайных величин определяется следующим образом (несмещенная оценка)
Если размер выборки относительно ограничен, то для более точного расчета применяется формула смещенной (исправленной) ковариации:
Слайд 7
Показатели вариации
Коэффициент корреляции
Коэффициент корреляции– это безразмерная величина, которая может принимать
значения из отрезка :
1– имеет место абсолютная положительная корреляция между рассматриваемыми величинами
-1– имеет место абсолютная отрицательная корреляция между рассматриваемыми величинами
0 – линейная корреляционная связь отсутствует.
1– имеет место абсолютная положительная корреляция между рассматриваемыми величинами
-1– имеет место абсолютная отрицательная корреляция между рассматриваемыми величинами
0 – линейная корреляционная связь отсутствует.
Слайд 9Операции с данными
При вычислении ковариационной и корреляционной матриц используются операции
вычитания средних (центрирование) и деления на стандарты (нормирование).
Операция нормирования в пространстве соответствует изменению масштабов по всем осям координат так, чтобы величина рассеяния, характеризуемая величиной дисперсии, стала равной единице.
Операция нормирования в пространстве соответствует изменению масштабов по всем осям координат так, чтобы величина рассеяния, характеризуемая величиной дисперсии, стала равной единице.
Слайд 10Ковариационная матрица
При вычислении ковариационной матрицы используется операция «центрирование».
Слайд 13Вычисление корреляционной матрицы
При вычисление корреляционной матрицы используются операции центрирование и
нормирование
- диагональная матрица (нормирование)
Слайд 15Матрица нормированных вторых моментов
При вычислении матрицы нормированных начальных вторых моментов
используется операция нормирование
Слайд 20
Алгоритм вычисления собственных векторов
1. Выбрать произвольное начальное (нулевое) приближение собственного
вектора
2. Найти .
Положить k=0
Вычислить первое приближение собственного вектора .
Слайд 21
Алгоритм вычисления собственных векторов
3. Найти .
Вычисляется норма ошибки
Вычисляем k+1
приближение собственного вектора .
,
Полагаем k=k+1.
4. Шаг 3 повторяется пока
Слайд 22Свойства собственных векторов.
Матрица n x n имеет n собственных векторов.
Если собственный вектор умножить на ненулевой коэффициент, то результирующий вектор также является собственным вектором.
Собственный вектор
Слайд 25Упражнение. Для следующей квадратной матрицы определить какие векторы являются собственными
Векторы
