- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Координатный метод (ключевые задачи). Готовимся к ЕГЭ презентация
Содержание
- 1. Координатный метод (ключевые задачи). Готовимся к ЕГЭ
- 2. Координатный метод может быть использован для нахождения:
- 3. Нахождение координат точки. Нахождение угла
- 4. Справочные материалы. Как вычислить координаты внутренней точки
- 5. Тренировочные упражнения. Прямоугольный параллелепипед Правильная шестиугольная призма
- 6. L К А В С D А1
- 7. L К А В С D А1
- 8. B В правильной шестиугольной
- 9. O К А SABCD – правильная пирамида,
- 10. O К А В С D S
- 11. O К А В С D S
- 12. O К А SABC – правильная
- 13. O К А В С S
- 14. O К А В С S L
- 15. O К А В С S L
- 16. Алгоритм. Нахождение угла между прямыми. Назад
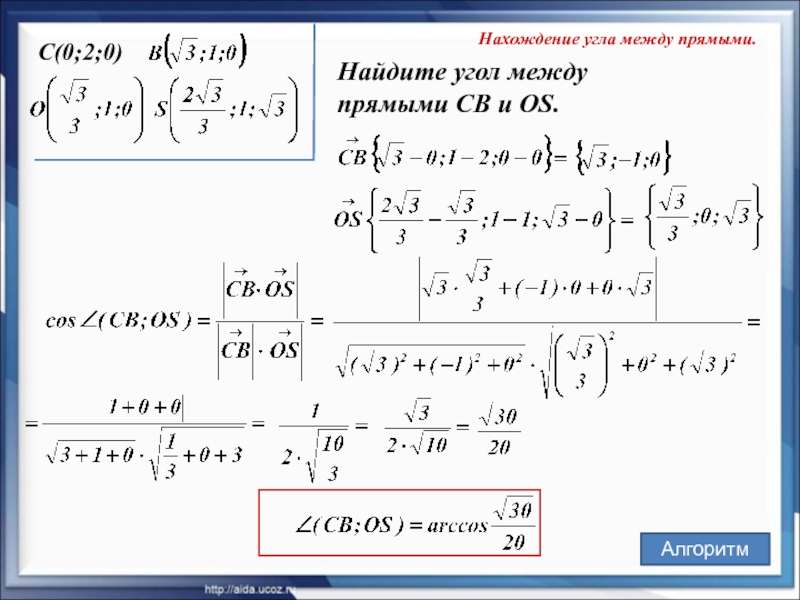
- 17. Нахождение угла между прямыми. C(0;2;0) Найдите
- 18. Алгоритм. Вывод уравнения плоскости ax+by+cz+d=0. Назад
- 19. Вывод уравнения плоскости. Запишите уравнение плоскости (АВС) Алгоритм
- 20. Вывод уравнения плоскости. Запишите уравнение плоскости (АВС) Алгоритм
- 21. Алгоритм. Нахождение расстояния от точки до
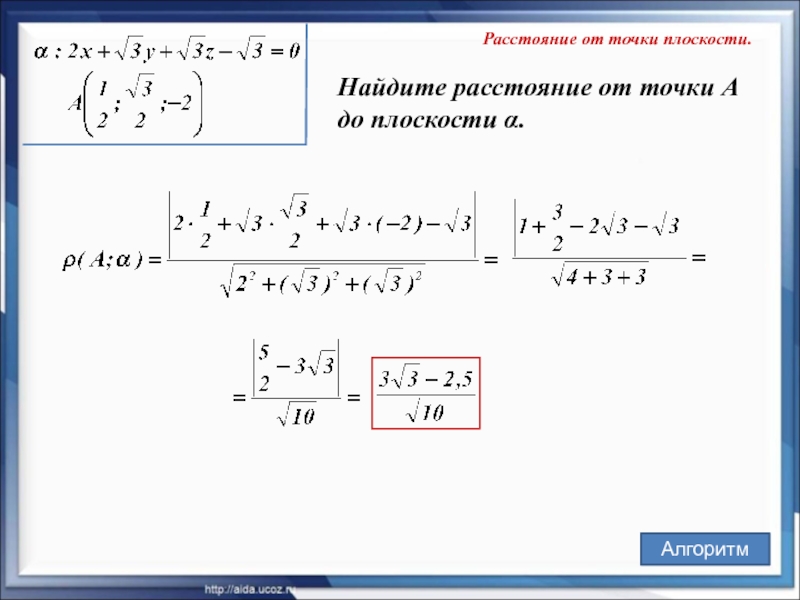
- 22. Расстояние от точки плоскости. Найдите расстояние от точки А до плоскости α. Алгоритм
- 23. Алгоритм. Нахождение угла между плоскостями. Назад
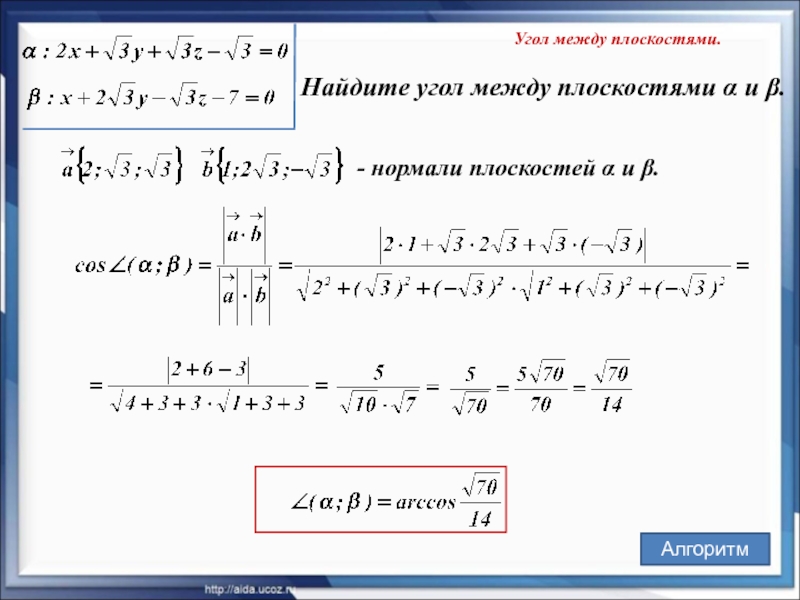
- 24. Угол между плоскостями. Найдите угол между
- 25. Алгоритм. Нахождение угла между прямой и
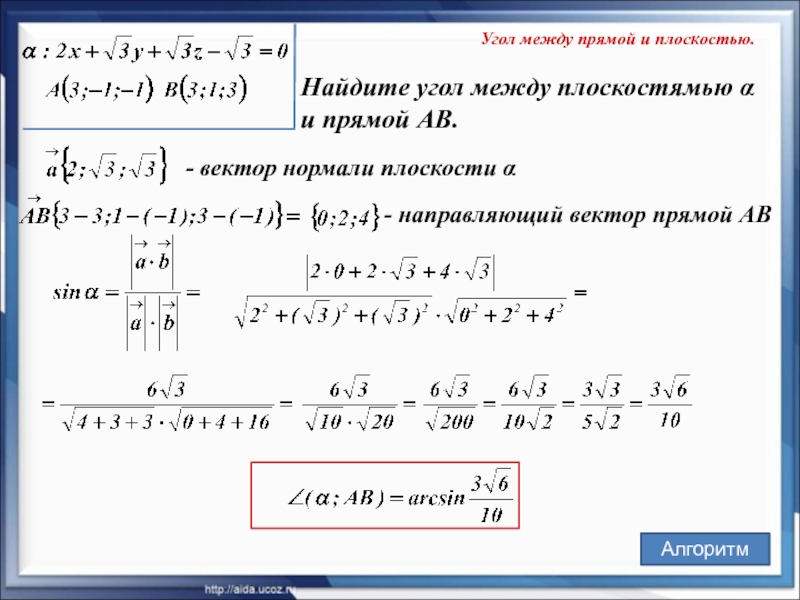
- 26. Угол между прямой и плоскостью. Найдите
- 27. Пусть
- 28. Нахождение угла между прямыми. Найдите расстояние
- 29. Нахождение угла между прямыми. Найдите расстояние
- 30. * При создании презентации использовано пособие: http://www.alleng.ru/d/math/math784.htm
Слайд 1Готовимся к ЕГЭ.
Задача С2.
Координатный метод
(ключевые задачи).
МБОУ г. Мурманска
Шахова Татьяна Александровна
Слайд 2Координатный метод может быть использован для нахождения:
длины отрезка (расстояния между
расстояния между прямыми;
расстояния от точки до прямой и плоскости;
угла между прямыми;
угла между прямой и плоскостью;
угла между плоскостями;
нахождения площади сечения.
http://le-savchen.ucoz.ru/load/4-1-0-183
Первоначальные сведения
о прямоугольной системе координат
смотри по адресу:
Слайд 3 Нахождение координат точки.
Нахождение угла между прямыми.
Вывод уравнения плоскости.
Нахождение угла между плоскостями.
Нахождение угла между прямой и плоскостью.
Нахождение расстояния между прямыми.
Ключевые задачи.
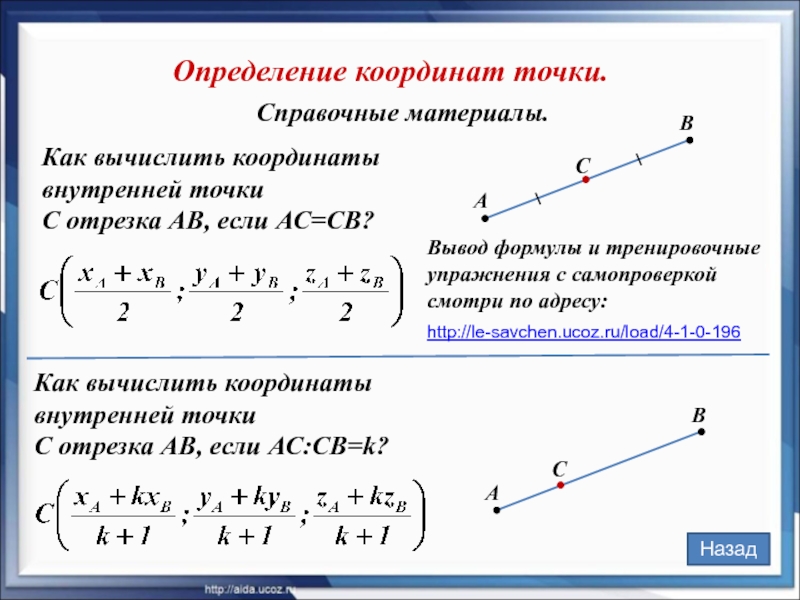
Слайд 4Справочные материалы.
Как вычислить координаты внутренней точки
С отрезка АВ, если АС:СВ=k?
Как вычислить координаты внутренней точки
С отрезка АВ, если АС=СВ?
Определение координат точки.
Вывод формулы и тренировочные
упражнения с самопроверкой
смотри по адресу:
http://le-savchen.ucoz.ru/load/4-1-0-196
Назад
А
В
С
А
В
С
Слайд 5Тренировочные упражнения.
Прямоугольный параллелепипед
Правильная шестиугольная призма
Правильная четырехугольная пирамида
Правильная треугольная пирамида
Определение координат точки.
Слайд 6L
К
А
В
С
D
А1
D1
С1
В1
X
Y
Z
Y
А1(4;0;2)
2
2
4
B1(?;?;?)
B1(4;2;2)
М
К(?;?;?)
C(?;?;?)
C(0;2;0)
К(4;1;2)
А1(?;?;?)
А(?;?;?)
А(4;0;0)
M(?;?;?)
ABCDA1B1C1D1 – прямоугольный параллелепипед. AB=2, AD=4, AA1=2, А1К=КВ1, АМ:МС=2:3, KL=LM .
Определите координаты точек A, C, А1, В1, К, М, L.
?
?
Определение координат точки.
Задачи
Слайд 7L
К
А
В
С
D
А1
D1
С1`
В1
X
Y
Z
Y
2
2
4
М
L(?;?;?)
К(4;1;2)
Определение координат точки.
ABCDA1B1C1D1 – прямоугольный параллелепипед. AB=2, AD=4, AA1=2, А1К=КВ1, АМ:МС=2:3,
Определите координаты точек A, C, А1, В1, К, М, L.
?
Задачи
Слайд 8
B
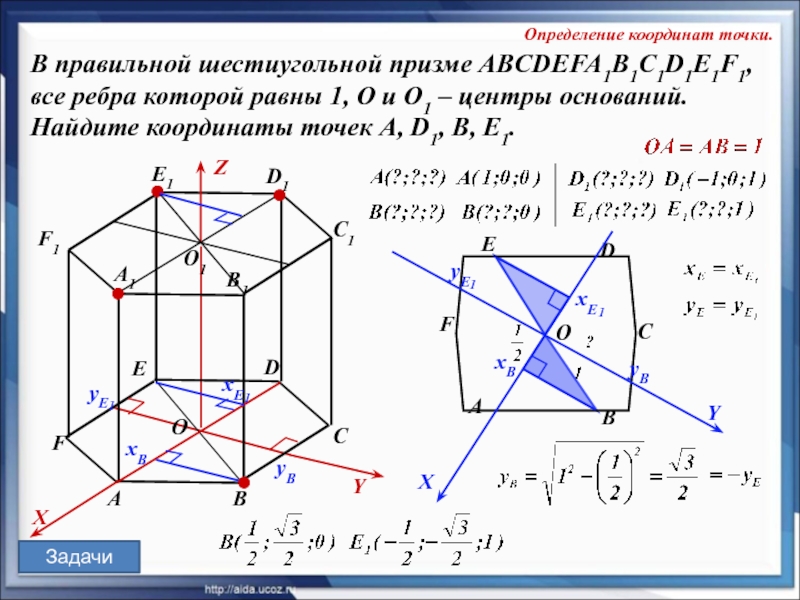
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1, все ребра которой равны 1, O
A
A1
B1
C
C1
D1
D
E
F1
F
E1
F
A
B
C
D
Е
X
Y
Z
X
Y
хЕ
yЕ
хB
yB
хB
хЕ
yB
yЕ
О
О1
Определение координат точки.
О
1
1
1
1
Задачи
Слайд 9O
К
А
SABCD – правильная пирамида, все ребра которой равны 1. SL=LC, SK:KO=1:2,
Определите координаты точек C, S, O, L, К, M.
В
С
D
S
L
X
Y
Z
Y
М
S(?;?;?)
C(?;?;?)
C(0;1;0)
S(?;?;1)
X
Y
O
yO(yS )
L(?;?;?)
xO(xS )
D
А
В
С
?
Определение координат точки.
О(?;?;?)
О(?;?;0)
Слайд 10O
К
А
В
С
D
S
L
X
Y
Z
Y
М
K(?;?;?)
?
SABCD – правильная пирамида, все ребра которой равны 1. SL=LC, SK:KO=1:2,
Определите координаты точек C, S, O, L, К, M.
Определение координат точки.
Задачи
Слайд 11O
К
А
В
С
D
S
L
X
Y
Z
Y
М
C(0;1;0)
M(?;?;?)
?
SABCD – правильная пирамида, все ребра которой равны 1. SL=LC, SK:KO=1:2,
Определите координаты точек C, S, O, L, К, M.
Определение координат точки.
Задачи
Слайд 12
O
К
А
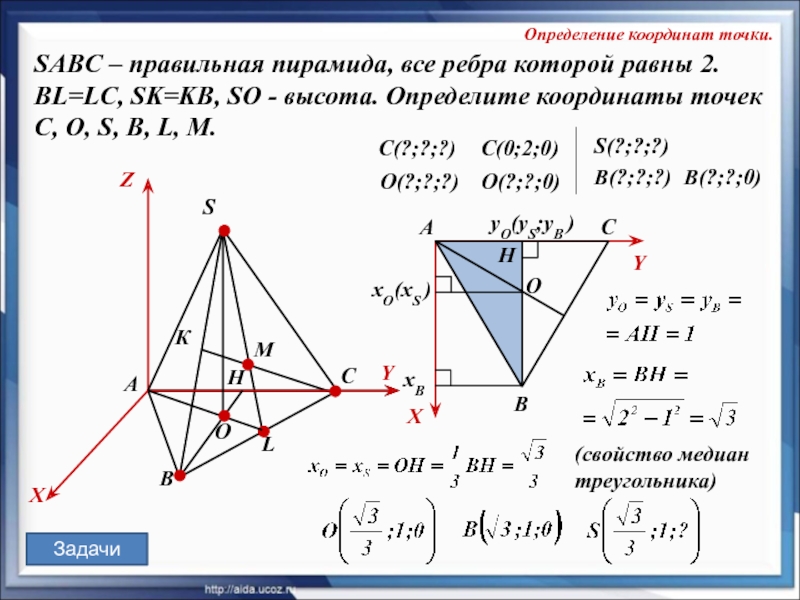
SABC – правильная пирамида, все ребра которой равны 2. BL=LC, SK=KB,
В
С
А
S
L
X
Z
Y
М
C(0;2;0)
C(?;?;?)
X
Y
O
xO(xS )
yO(yS;уВ )
В
С
H
H
(свойство медиан
треугольника)
О(?;?;?)
S(?;?;?)
Определение координат точки.
xВ
О(?;?;0)
В(?;?;?)
В(?;?;0)
Задачи
Слайд 13
O
К
А
В
С
S
L
X
Z
Y
М
X
SABC – правильная пирамида, все ребра которой равны 2. BL=LC, SK=KB,
Определение координат точки.
Из треугольника ВОS
Задачи
Слайд 14O
К
А
В
С
S
L
X
Z
Y
М
C(0;2;0)
X
(середина отрезка ВС)
L(?;?;?)
?
SABC – правильная пирамида, все ребра которой равны 2.
Определение координат точки.
Задачи
Слайд 15O
К
А
В
С
S
L
X
Z
Y
М
X
М – точка пересечения медиан
треугольника BSC =>
М(?;?;?)
SМ:ML=2:1
?
SABC – правильная пирамида,
Определение координат точки.
Задачи
Слайд 18
Алгоритм.
Вывод уравнения плоскости ax+by+cz+d=0.
Назад
А
В
С
Подставить в уравнение плоскости
координаты точек А,В и С.
Решить
либо а, с и d через b, либо c, b и d через a в зависимости от
составленной системы.
3) Подставить выраженные коэффициенты в исходное
уравнение и преобразовать к удобному виду.
Слайд 21
Алгоритм.
Нахождение расстояния от точки до плоскости.
Назад
А
α
Если плоскость α задана уравнением
то расстояние
плоскости α можно найти
по формуле:
Слайд 23
Алгоритм.
Нахождение угла между плоскостями.
Назад
Если плоскости α и β заданы уравнениями
β
α
соответственно, то
и
-
- вектор нормали плоскости β.
Угол между плоскостями равен углу
между нормалями этих плоскостей.
Алгоритм
Слайд 24Угол между плоскостями.
Найдите угол между плоскостями α и β.
Алгоритм
- нормали плоскостей
Слайд 25
Алгоритм.
Нахождение угла между прямой и плоскостью.
Назад
А
α
Если плоскость α задана уравнением
направляющий вектор
АВ имеет координаты
В
- вектор нормали плоскости α,
то угол между прямой АВ и
плоскостью α можно по формуле:
?
Слайд 26Угол между прямой и плоскостью.
Найдите угол между плоскостямью α
и прямой
Алгоритм
- вектор нормали плоскости α
- направляющий вектор прямой АВ
Слайд 27Пусть
условие:
Алгоритм.
Нахождение расстояния между прямыми.
Назад
B
C
А
D
М
К
1) Определить координаты направляющих векторов и .
2) Из системы определить координаты , затем найти
Замечание: для записи координат точек М и К воспользоваться формулой:
Если АМ:МВ=k, то
Слайд 28Нахождение угла между прямыми.
Найдите расстояние между
прямыми AC и BD.
Алгоритм
B
C
А
D
М
К
Пусть
АМ:МС=k, BK:KD=n,
Если
то