- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Комплексные числа презентация
Содержание
- 1. Комплексные числа
- 2. После изучения темы «Комплексные числа учащиеся должны:
- 3. Сложение, умножение Вычитание, деление, извлечение
- 4. Минимальные условия, которым должны удовлетворять комплексные числа:
- 5. Мнимые числа i = -1, i
- 6. Комплексные числа Определение 1. Комплексным числом называют
- 7. Классификация комплексных чисел Комплексные числа a +
- 8. Арифметические операции над комплексными числами (а +
- 9. Сопряженные комплексные числа Определение: Если у комплексного
- 10. Свойства сопряженных чисел Сумма и произведение двух
- 11. Свойства сопряженных чисел Число, сопряженное п-ой степени
- 12. Степени мнимой единицы По определению первой степенью
- 13. Извлечение квадратных корней из комплексных чисел в
- 14. Геометрическое изображение комплексных чисел. Комплексному числу z
- 15. Тригонометрическая форма комплексного числа
- 16. Извлечение корня из комплексного числа. Теорема. Для
Слайд 2После изучения темы «Комплексные числа учащиеся должны:
Знать:
алгебраическую, геометрическую и тригонометрическую формы
Уметь:
производить над комплексными числами операции сложения, умножения, вычитания, деления, возведения в степень, извлечение корня из комплексного числа;
переводить комплексные числа из алгебраической формы в геометрическую и тригонометрическую;
пользоваться геометрической интерпретацией комплексных чисел;
в простейших случаях находить комплексные корни уравнений с действительными коэффициентами.
Слайд 3
Сложение, умножение
Вычитание, деление, извлечение корней
Сложение, вычитание, умножение
Деление, извлечение корней
Сложение, вычитание, умножение,
Извлечение корней из неотрицательных чисел
Сложение, вычитание, умножение, деление, извлечение корней из неотрицательных чисел
Извлечение корней из произвольных чисел
Комплексные числа, C
Все операции
Слайд 4Минимальные условия, которым должны удовлетворять комплексные числа:
С1) Существует квадратный корень из
С2) Множество комплексных чисел содержит все действительные числа.
С3) Операции сложения, вычитания, умножения и деления комплексных чисел удовлетворяют обычным законам арифметических действий (сочетательному, переместительному, распределительному).
Выполнение этих минимальных условий позволяет определить все множество С комплексных чисел.
Слайд 5
Мнимые числа
i = -1, i – мнимая единица
i, 2i, -0,3i —
Арифметические операции над чисто мнимыми числами выполняются в соответствии с условием С3.
где a и b — действительные числа.
В общем виде правила арифметических операций с чисто мнимыми числами таковы:
Слайд 6Комплексные числа
Определение 1. Комплексным числом называют сумму действительного числа и чисто
Определение 2. Два комплексных числа называют равными, если равны их действительные части и равны их мнимые части:
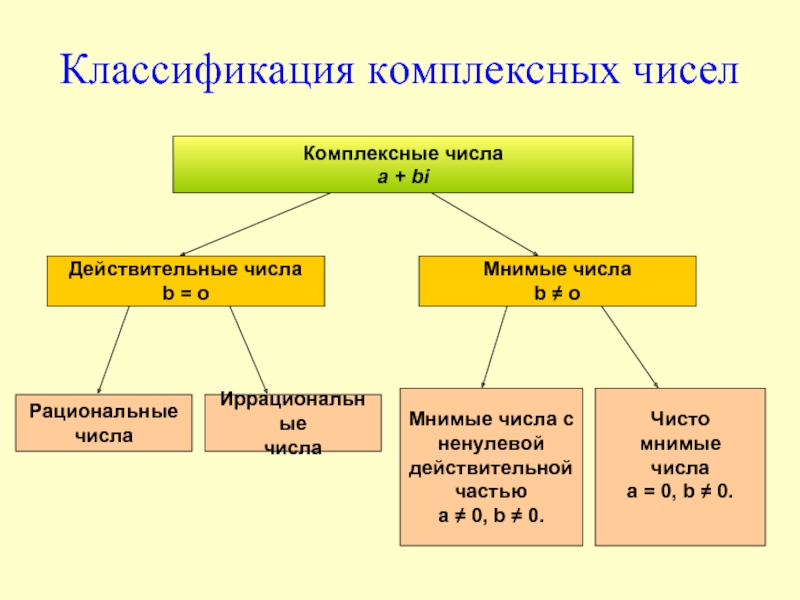
Слайд 7Классификация комплексных чисел
Комплексные числа
a + bi
Действительные числа
b = o
Мнимые числа
b ≠
Рациональные
числа
Иррациональные
числа
Мнимые числа с
ненулевой
действительной
частью
a ≠ 0, b ≠ 0.
Чисто
мнимые
числа
a = 0, b ≠ 0.
Слайд 8Арифметические операции над комплексными числами
(а + bi) + (c + di)
(а + bi) - (c + di) = (а - с) + (b - d)i
(а + bi)·(с + di) = (ac - bd) + (ad + bc)i
Слайд 9Сопряженные комплексные числа
Определение: Если у комплексного числа сохранить действительную часть и
Если данное комплексное число обозначается буквой z, то сопряженное число обозначается :
:
.
Из всех комплексных чисел действительные числа (и только они) равны своим сопряженным числам.
Числа a + bi и a - bi называются взаимно сопряженными комплексными числами.
Слайд 10Свойства сопряженных чисел
Сумма и произведение двух сопряженных чисел есть число действительное.
Число,
Число, сопряженное разности двух комплексных чисел, равно разности сопряженных данным числам.
Число, сопряженное произведению двух комплексных чисел, равно произведению сопряженных данным числам.
Слайд 11Свойства сопряженных чисел
Число, сопряженное п-ой степени комплексного числа z, равно п-ой
Число, сопряженное частному двух комплексных чисел, из которых делитель отличен от нуля, равно частному сопряженных чисел, т.е.
Слайд 12Степени мнимой единицы
По определению первой степенью числа i является само число
.
Более высокие степени числа i находятся следующим образом:
i4 = i3 ∙ i = -∙i2= 1;
i5 = i4 ∙ i = i;
i6 = i5 ∙ i = i2= - 1 и т.д.
i1 = i, i2 = -1
Очевидно, что при любом натуральном n
i4n = 1; i4n+1 = i;
i4n +2 = - 1 i4n+3 = - i.
Слайд 13Извлечение квадратных корней из комплексных чисел в алгебраической форме.
Определение. Число w
Теорема. Пусть z=a+bi – отличное от нуля комплексное число. Тогда существуют два взаимно противоположных комплексных числа, квадраты которых равны z. Если b≠0, то эти два числа выражаются формулой:
Слайд 14Геометрическое изображение комплексных чисел.
Комплексному числу z на координатной плоскости соответствует точка
Часто вместо точек на плоскости берут их радиусы-векторы
Определение: Модулем комплексного числа z = a + bi называют неотрицательное число ,
равное расстоянию от точки М до начала координат
b
a
М (a, b)
y
x
O
φ
Слайд 15
Тригонометрическая форма комплексного числа
где φ – аргумент комплексного числа,
r =
Слайд 16Извлечение корня из комплексного числа.
Теорема. Для любого натурального числа n и
Если