- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Показательные неравенства, их типы и методы решения презентация
Содержание
- 1. Показательные неравенства, их типы и методы решения
- 2. Вычеркните в каждом ряду лишнее
- 3. монотонно убывает на R
- 5. ?
- 8. ?
- 9. ?
- 10. Пусть а – данное положительное,
- 11. Решением неравенства с неизвестным х называют
- 12. Решить неравенство – значит, найти все его решения или показать, что их нет.
- 16. х0 х1 y=b, b>0
- 18. возрастает на всей области определения, Решение:
- 19. Решение: убывает на всей области определения,
- 20. Решение: возрастает на всей области определения,
- 21. возрастает на всей области определения,
- 23. возрастает на всей области определения
- 24. Вернёмся к переменной х возрастает при всех х из области определения
- 28. Вернёмся
- 31. Показательные неравенства их типы
Слайд 2
Вычеркните
в каждом ряду лишнее (по смыслу составления ряда) число.
Концентрация внимания
N = (число верно выписанных
чисел) х 0,125 х 100%.
Верным должен быть следующий ряд чисел:
13; 3; 9; 35; 24; 17; 45; 7.
Слайд 3монотонно убывает на R
Ось Ох является горизонтальной асимптотой
монотонно возрастает на R
8.
7. Асимптота
6. Экстремумы
5. Монотонность
4. Четность, нечетность
3. Промежутки сравнения значений функции с единицей
2. Область значений функции
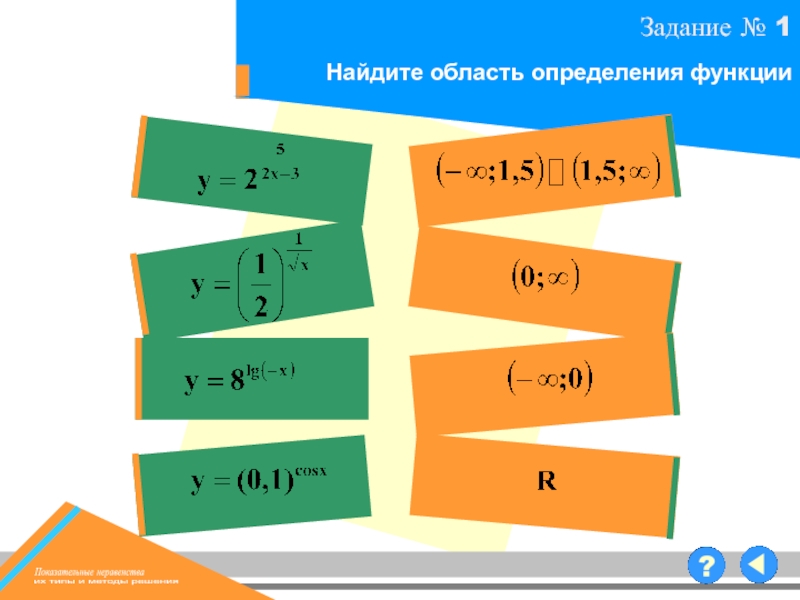
1. Область определения функции
С в о й с т в а показательной функции
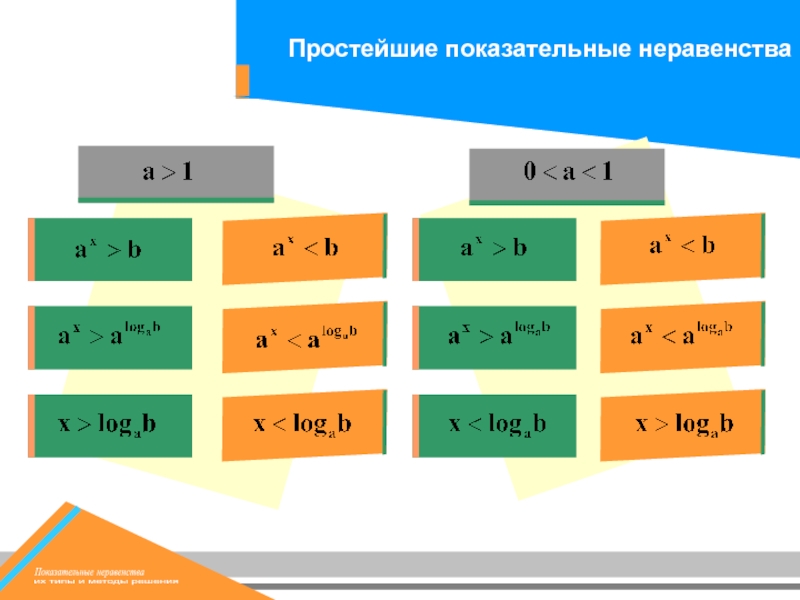
Показательные неравенства
их типы и методы решения
Показательная функция экстремумов не имеет
Функция не является ни чётной, ни нечётной (функция общего вида).
Слайд 10
Пусть а – данное положительное, не равное единице число и b
Слайд 11
Решением неравенства с неизвестным х называют число х0, при подстановке которого
Слайд 15
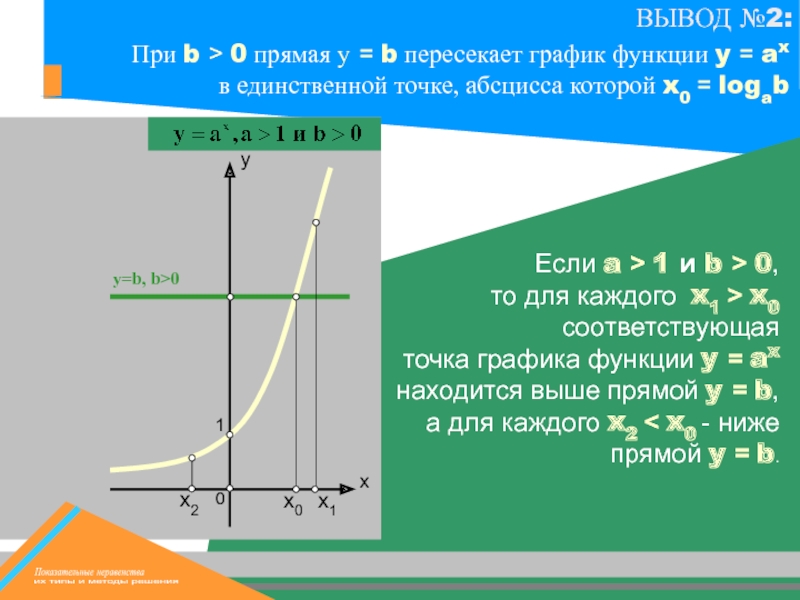
х0
х1
y=b, b>0
1
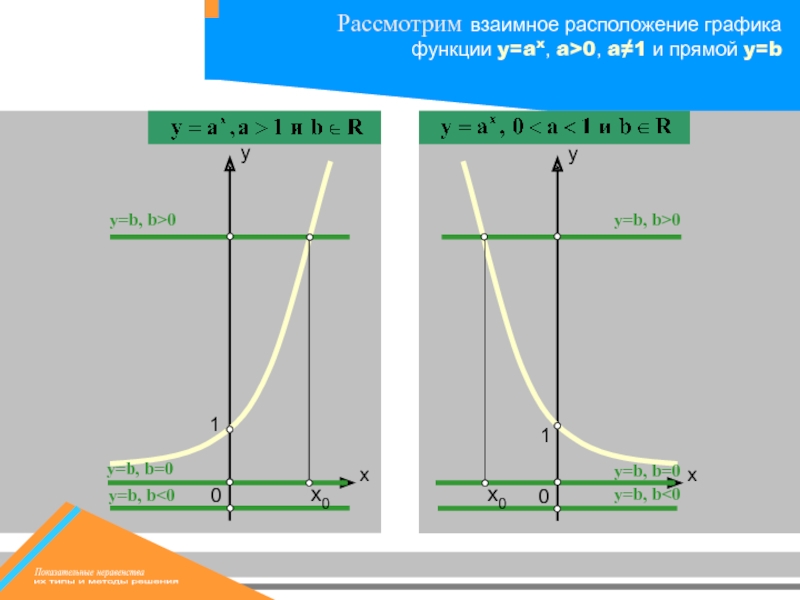
Если a > 1 и b > 0,
то для
точка графика функции y = ax находится выше прямой y = b,
а для каждого x2 < x0 - ниже прямой y = b.
При b > 0 прямая у = b пересекает график функции y = ax в единственной точке, абсцисса которой x0 = logab
х2
Слайд 16
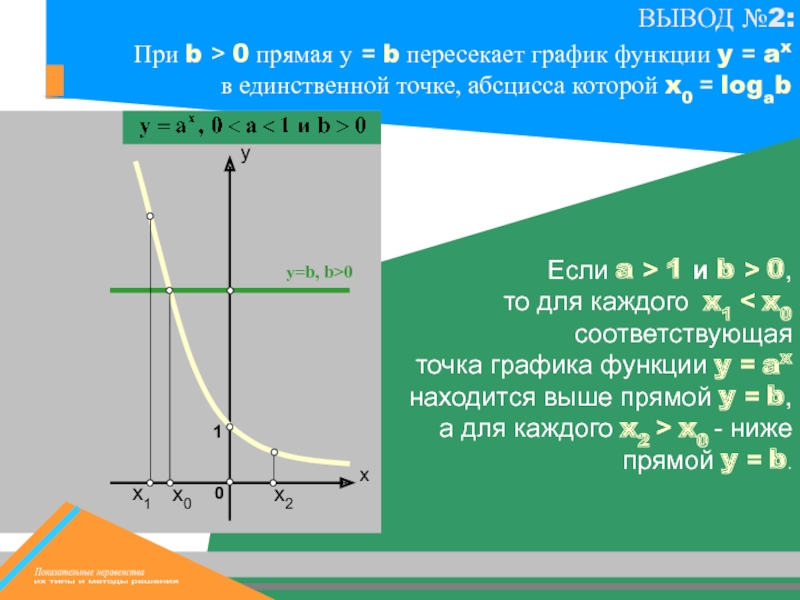
х0
х1
y=b, b>0
х2
Если a > 1 и b > 0,
то для
точка графика функции y = ax находится выше прямой y = b, а для каждого x2 > x0 - ниже прямой y = b.
1
При b > 0 прямая у = b пересекает график функции y = ax в единственной точке, абсцисса которой x0 = logab
Слайд 30
Проверка
Проверка показала, что х=1, х=3, х=1,5 являются решениями уравнения, а х=2
Слайд 31
Показательные неравенства
их типы и методы решения
Лицей-интернат естественных наук при
Выполнил Бобров Р.С.
Руководитель Калугина Е.Е.