привело стремление решить уравнение х2 +1=0 и извлечь корень из отрицательного числа.
Комплексным числом называется выражение вида z=x+iy, где x, y– действительные числа, i − мнимая единица (i2=−1).
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Комплексные числа презентация
Содержание
- 1. Комплексные числа
- 2. Числа x, y называются соответственно действительной и
- 3. Два комплексных числа считаются равными, если равны
- 4. Комплексное число изображается точкой М плоскости
- 5. Наряду с алгебраической формой комплексного числа z=x+iy
- 6. Пример. Записать комплексное число в тригонометрической и показательной формах.
- 7. §2. Основные действия над комплексными числами Операции
- 8. 2. Умножение двух комплексных чисел в алгебраической
- 9. 3. Деление комплексных чисел При делении двух
- 10. Пример. Вычислить
- 11. Теорема. При делении двух комплексных чисел в
- 12. 4. Возведение в степень комплексного числа Возведение
- 13. При возведении комплексного числа в бóльшую степень
- 14. Пример. Вычислить z6, если
- 15. 5. Извлечение корня n-й степени из комплексного
- 16. Придавая k значения 0, 1, 2,….,n−1, получим
- 17. Аналогично, Таким образом, для любого z≠0
- 18. Замечание. Если нужно извлечь корень квадратный, то
Слайд 1Комплексные числа
§1. Определение, изображение, формы записи комплексного числа
К понятию комплексного числа
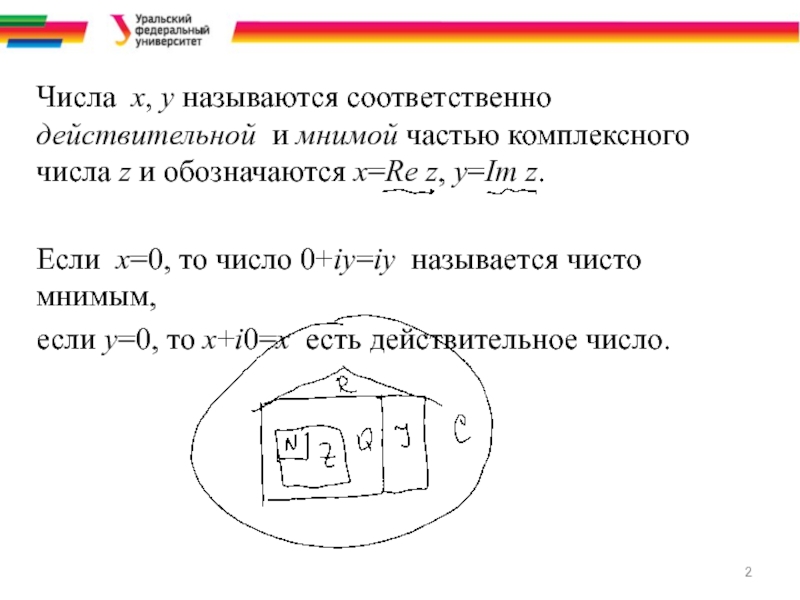
Слайд 2Числа x, y называются соответственно действительной и мнимой частью комплексного числа
z и обозначаются x=Re z, y=Im z.
Если x=0, то число 0+iy=iy называется чисто мнимым,
если y=0, то x+i0=x есть действительное число.
Если x=0, то число 0+iy=iy называется чисто мнимым,
если y=0, то x+i0=x есть действительное число.
Слайд 3Два комплексных числа считаются равными, если равны их действительные части и
равны их мнимые части, т.е.
Комплексные числа z=x+iy и отличающиеся знаком мнимой части, называются комплексно-сопряженными.
Комплексные числа z=x+iy и отличающиеся знаком мнимой части, называются комплексно-сопряженными.
Слайд 4Комплексное число изображается точкой М плоскости с координатами x, y
или ее радиус-вектором
Длина вектора называется модулем комплексного числа z и обозначается |z|, r или ρ:
Угол φ между радиус-вектором
и положительным направлением
оси Ox называют аргументом комплексного числа z.
Угол φ определяется неоднозначно, с точностью до слагаемого 2πk; договоримся брать то значение φ, которое заключено между −π и π и обозначать его
Длина вектора называется модулем комплексного числа z и обозначается |z|, r или ρ:
Угол φ между радиус-вектором
и положительным направлением
оси Ox называют аргументом комплексного числа z.
Угол φ определяется неоднозначно, с точностью до слагаемого 2πk; договоримся брать то значение φ, которое заключено между −π и π и обозначать его
Слайд 5Наряду с алгебраической формой комплексного числа z=x+iy рассмотрим еще две формы
записи.
Так как то комплексное число z=x+iy можно записать в тригонометрической форме:
Введя функцию комплексное число можно записать в показательной форме:
Итак, имеем три формы записи комплексного числа
Так как то комплексное число z=x+iy можно записать в тригонометрической форме:
Введя функцию комплексное число можно записать в показательной форме:
Итак, имеем три формы записи комплексного числа
Слайд 7§2. Основные действия над комплексными числами
Операции сложения, вычитания, умножения комплексных чисел
определяются следующим естественным образом.
1. При сложении (вычитании) двух комплексных чисел складываются (соответственно вычитаются) их действительные и мнимые части, т.е.
1. При сложении (вычитании) двух комплексных чисел складываются (соответственно вычитаются) их действительные и мнимые части, т.е.
Слайд 82. Умножение двух комплексных чисел в алгебраической форме определяется по правилам
умножения двучленов с учетом равенства i2=−1, т.е.
Теорема. При умножении двух комплексных чисел в тригонометрической форме их модули умножаются, а аргументы складываются:
Аналогично, в показательной форме
Теорема. При умножении двух комплексных чисел в тригонометрической форме их модули умножаются, а аргументы складываются:
Аналогично, в показательной форме
Слайд 93. Деление комплексных чисел
При делении двух комплексных чисел в алгебраической форме
нужно числитель и знаменатель
дроби умножить на число, сопряженное
знаменателю; тогда делителем будет действительное число:
дроби умножить на число, сопряженное
знаменателю; тогда делителем будет действительное число:
Слайд 11Теорема. При делении двух комплексных чисел в тригонометрической и показательной формах
их модули делятся, а аргументы вычитаются, т.е.
Слайд 124. Возведение в степень комплексного числа
Возведение в степень комплексного числа в
алгебраической форме осуществляется по правилам возведения в степень двучлена с учетом того, что i2=−1, i3=i2i=−i, i4=(i2)2=(−1)2=1 и т.д.
Например, используя формулу куба разности, получим:
Например, используя формулу куба разности, получим:
Слайд 13При возведении комплексного числа в бóльшую степень удобно использовать его тригонометрическую
форму
Учитывая, что при умножении модули умножаются, а аргументы складываются, получим формулу Муавра:
Учитывая, что при умножении модули умножаются, а аргументы складываются, получим формулу Муавра:
Слайд 155. Извлечение корня n-й степени из комплексного числа
определяется как действие,
обратное возведению в степень, т.е. если
При извлечении корня из комплексного числа z удобно использовать тригонометрическую форму записи комплексного числа.
Пусть
Тогда
При извлечении корня из комплексного числа z удобно использовать тригонометрическую форму записи комплексного числа.
Пусть
Тогда
Слайд 16Придавая k значения 0, 1, 2,….,n−1, получим n различных значений корня
n−й степени из комплексного числа.
При других значениях k получим значения корня, совпадающие с уже найденными. Например, при k=n и при k=0 значения корней совпадают:
При других значениях k получим значения корня, совпадающие с уже найденными. Например, при k=n и при k=0 значения корней совпадают:
Слайд 17Аналогично,
Таким образом, для любого z≠0 корень степени n из числа
z имеет n различных значений.
Пример. Решить уравнение
Пример. Решить уравнение
Слайд 18Замечание. Если нужно извлечь корень квадратный, то можно и не пользоваться
соответствующей формулой.
Например,
Если вы не догадались о таком способе, то можно обозначить и возвести это равенство в квадрат:
Например,
Если вы не догадались о таком способе, то можно обозначить и возвести это равенство в квадрат: