- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основы математической обработки информации. Вариационные ряды и их характеристики. (Лекция 1) презентация
Содержание
- 1. Основы математической обработки информации. Вариационные ряды и их характеристики. (Лекция 1)
- 2. Целью дисциплины является: формирование знаний основ
- 3. Задачи дисциплины: формирование системы знаний и
- 4. Литература: Ермолаев, О. Ю. Математическая статистика для
- 5. «Зрелость науки обычно измеряется тем, в какой
- 6. Количественный анализ результатов исследования занимает важное место
- 7. Данные, полученные в результате психологического исследования, не
- 8. Правильное применение статистики позволяет ученому: 1) доказывать
- 9. Схема: ИССЛЕДОВАТЕЛЬ ↓ ПРЕДМЕТ ИССЛЕДОВАНИЯ (психические
- 10. Тема лекции: Вариационные ряды и их характеристики §1. Основные понятия
- 11. Обычно полученные в результате наблюдений данные представляют
- 12. Ряды распределения Рядом распределения называется упорядоченное распределение
- 13. Ряды распределения Распределение может быть по признакам,
- 14. Ряды распределения Ряды распределения единиц совокупности по признакам, имеющим количественное выражение, называются вариационными рядами
- 15. Элементы вариационного ряда: Варианты Частоты
- 16. Предположим, что изучается некоторая случайная величина Х
- 17. Определение. Различные значения признака, наблюдающиеся у
- 18. Частость – относительное выражение частоты, представляет собой
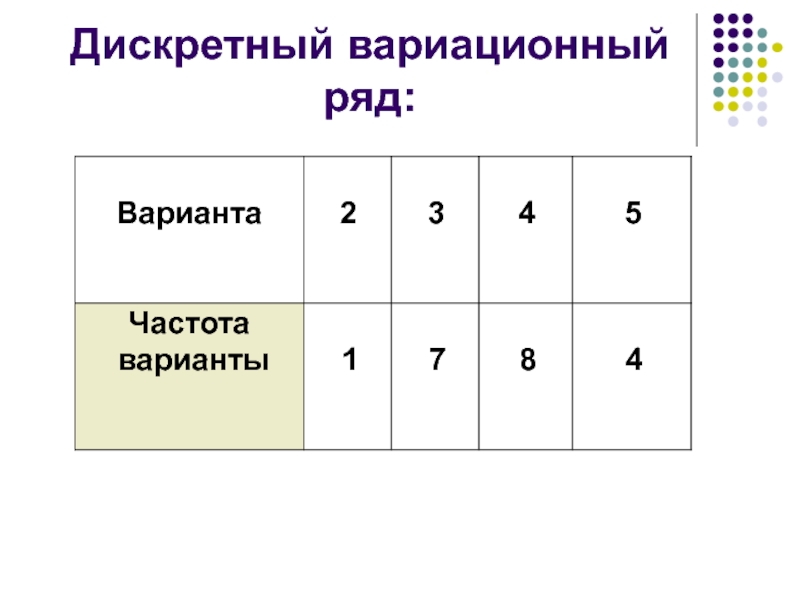
- 19. Определение. Дискретным вариационным рядом называется ранжированный
- 20. Дискретный вариационный ряд
- 21. Пример 1. 20 студентов на экзамене
- 22. Дискретный вариационный ряд:
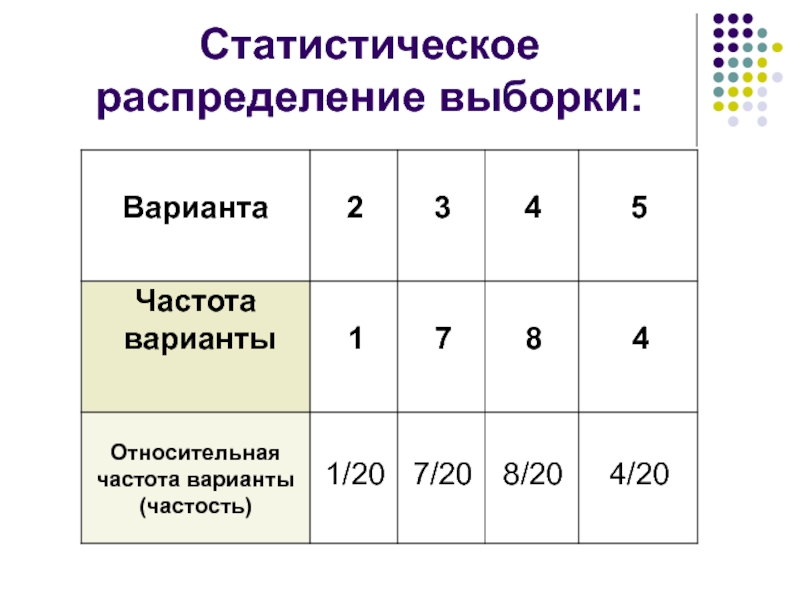
- 23. Статистическое распределение выборки:
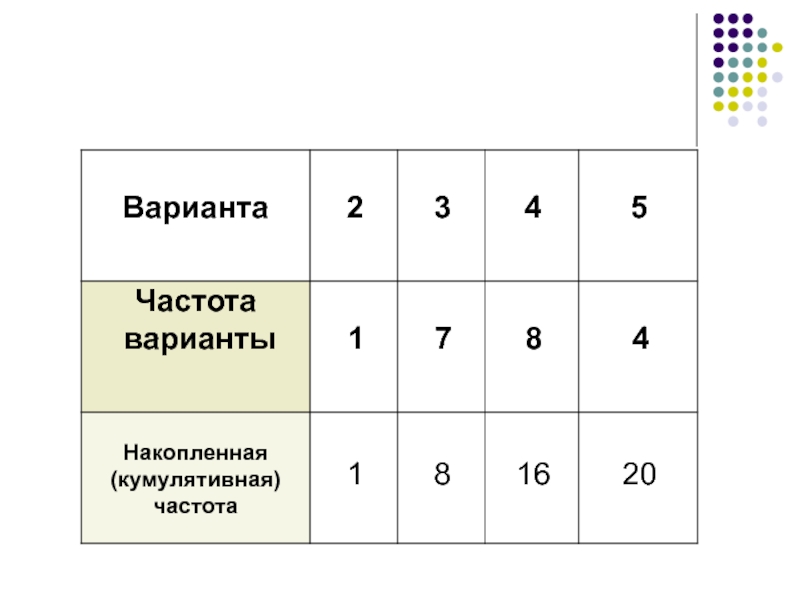
- 24. Накопленная (кумулятивная) частота – какое число
- 26. Если число различных значений признака (с.в.
- 27. Если весь промежуток изменения значений выборки, от
- 28. Интервальный статистический ряд
- 29. Пример 2. По результатам измерений получена выборка.
- 31. Вопросы: Сколько должно быть интервалов? Какова длина
- 32. Графическое изображение вариационных рядов
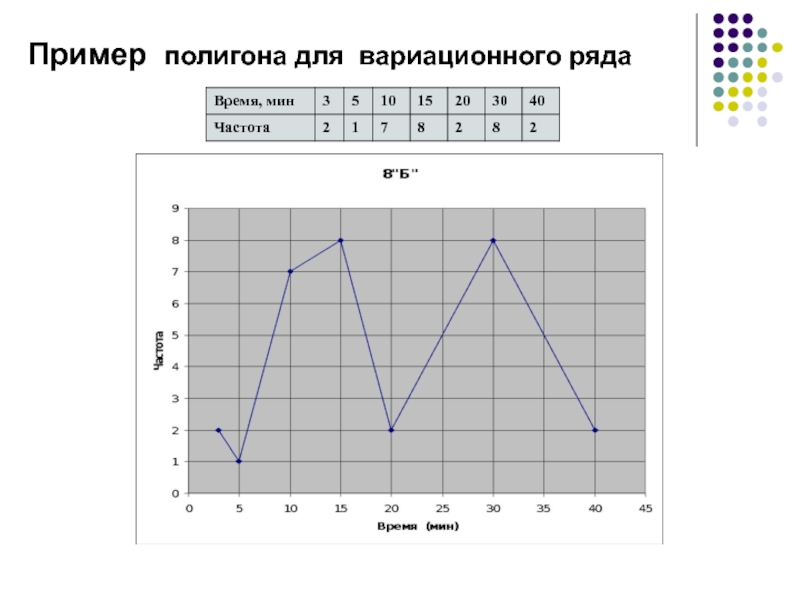
- 34. Пример полигона для вариационного ряда
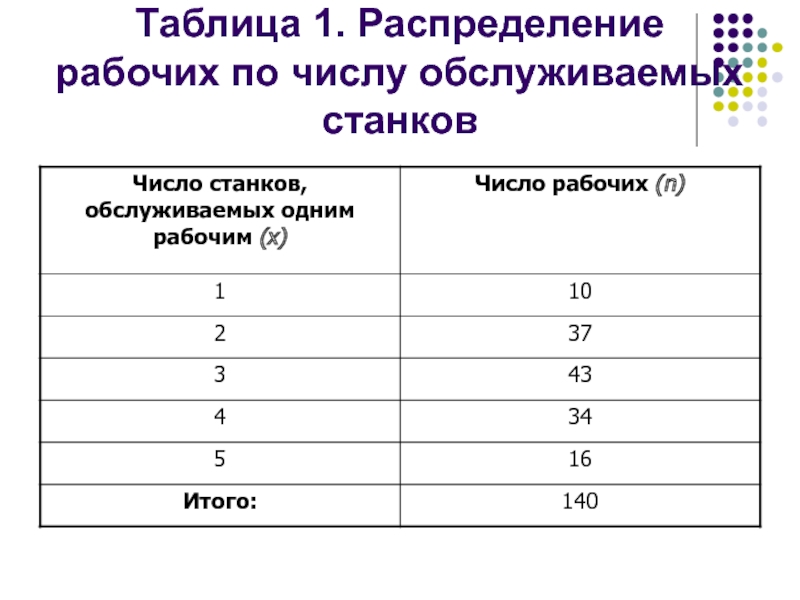
- 35. Таблица 1. Распределение рабочих по числу обслуживаемых станков
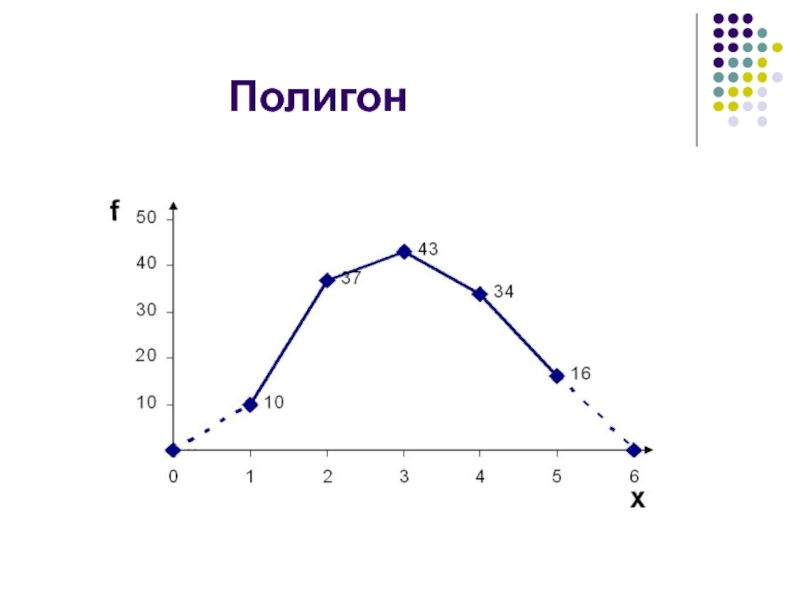
- 36. Полигон
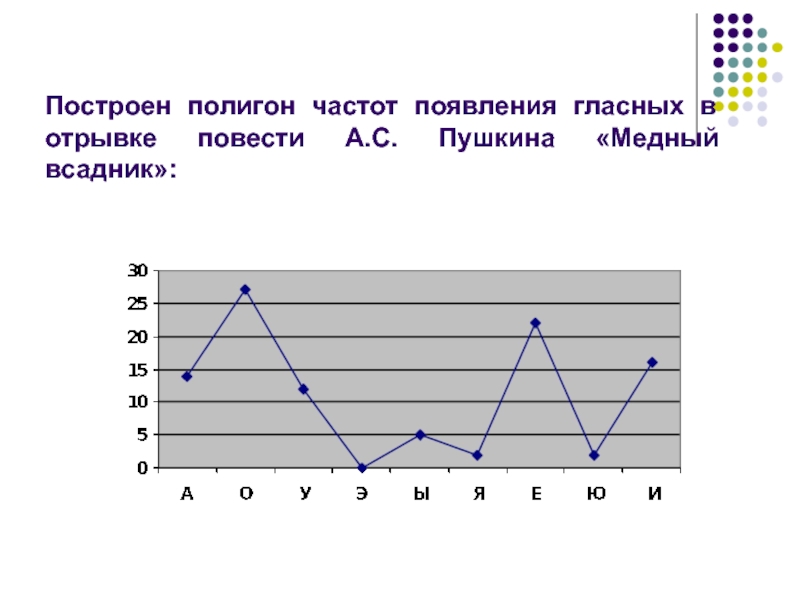
- 37. Построен полигон частот появления гласных в отрывке повести А.С. Пушкина «Медный всадник»:
- 38. Гистограмма
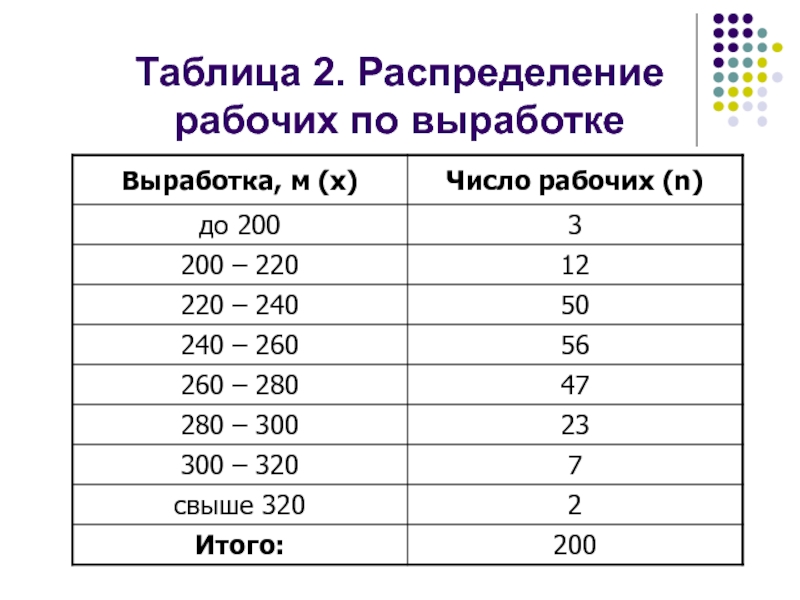
- 39. Таблица 2. Распределение рабочих по выработке
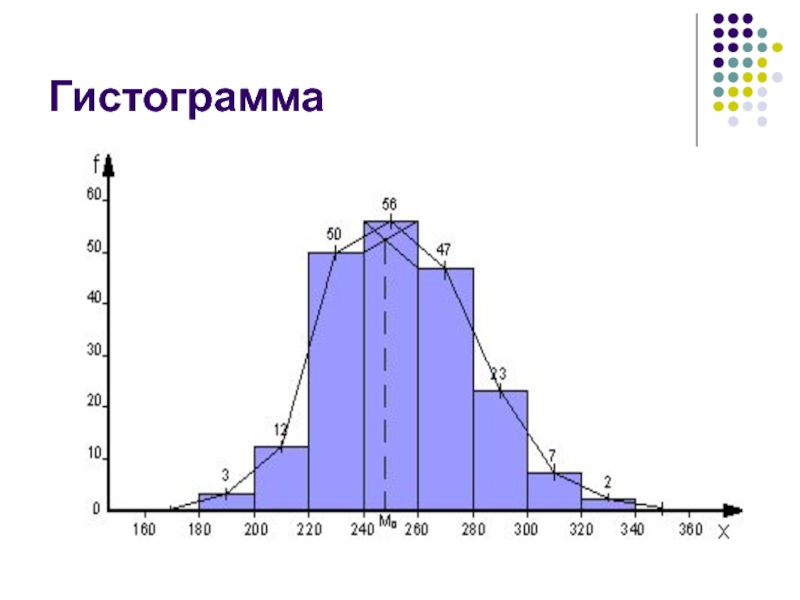
- 40. Гистограмма
- 41. Кумулята Кумулятивная кривая (кумулята) – кривая накопленных
- 42. Кумулята Для интервального вариационного ряда ломаная начинается
- 43. Кумулята
- 44. Числовые характеристики вариационного ряда: Средние величины Показатели вариации
- 45. Средние величины Средние величины характеризуют значение признака,
- 46. Средней арифметической вариационного ряда называется сумма
- 47. Мода Mo - это значение, которое встречается в выборке наиболее часто.
- 48. Медиана Me - это значение,
- 49. Показатели вариации Дисперсией вариационного ряда называется средняя
Слайд 2Целью дисциплины является:
формирование знаний основ классических методов математической обработки информации; навыков
Слайд 3Задачи дисциплины:
формирование системы знаний и умений, связанных с представлением информации
актуализация межпредметных знаний, способствующих пониманию особенностей представления и обработки информации средствами математики;
ознакомление с основными математическими моделями и типичными для соответствующей предметной области задачами их использования;
формирование системы математических знаний и умений, необходимых для понимания основ процесса математического моделирования и статистической обработки информации в профессиональной области.
Слайд 4Литература:
Ермолаев, О. Ю. Математическая статистика для психологов– М.: Московский психолого-социальный институт
Кремер, Н. Ш. Теория вероятностей и математическая статистика. Учебник для вузов - М. : ЮНИТИ-ДАНА, 2006.
Письменный, Д. Т. Конспект лекций по теории вероятностей, математической статистике и случайным процессам - М. : Айрис-пресс, 2008
Слайд 5«Зрелость науки обычно измеряется тем, в какой мере она использует математику.»
(С.С.
Слайд 6Количественный анализ результатов исследования занимает важное место в профессиональной деятельности педагога-
Слайд 7Данные, полученные в результате психологического исследования, не имеют практического значения без
интерпретации.
Математические методы обеспечивают познавательную потребность специалиста.
Описание каких-либо психологических явлений при помощи математических методов – это мощное средство их обобщения, способствующее теоретизации психологии как науки.
Слайд 8Правильное применение статистики позволяет ученому:
1) доказывать правильность и обоснованность используемых методических
2) строго обосновывать экспериментальные планы;
3) обобщать данные эксперимента;
4) находить зависимости между экспериментальными данными;
5) выявлять наличие существенных различий между группами испытуемых (например, экспериментальными и контрольными);
6) строить статистические предсказания;
7) избегать логических и содержательных ошибок и многое другое.
Слайд 9Схема:
ИССЛЕДОВАТЕЛЬ
↓
ПРЕДМЕТ ИССЛЕДОВАНИЯ (психические свойства, процессы, функции)
↓
ИСПЫТУЕМЫЙ (группа испытуемых)
↓
ЭКСПЕРИМЕНТ(измерение)
↓
ДАННЫЕ ЭКСПЕРИМЕНТА( числовые
↓
СТАТИСТИЧЕСКАЯ ОБРАБОТКА ДАННЫХ ЭКСПЕРИМЕНТА
↓
Результат статистической обработки эксперимента
↓
ВЫВОДЫ (печатный текст: отчет, статья, …)
↓
ПОЛУЧАТЕЛЬ НАУЧНОЙ ИНФОРМАЦИИ (руководитель , заказчик)
Слайд 11Обычно полученные в результате наблюдений данные представляют собой набор чисел. Просматривая
Слайд 12Ряды распределения
Рядом распределения называется упорядоченное распределение единиц совокупности на группы по
Слайд 13Ряды распределения
Распределение может быть по признакам, не имеющим количественной меры (атрибутивным),
Слайд 14Ряды распределения
Ряды распределения единиц совокупности по признакам, имеющим количественное выражение, называются
Слайд 16Предположим, что изучается некоторая случайная величина Х (некоторый признак).
С этой
Совокупность полученных значений
(1)
(некоторые значения могут совпадать) называется выборкой .
Слайд 17
Определение. Различные значения признака, наблюдающиеся у членов совокупности, называются вариантами, а
Слайд 18Частость –
относительное выражение частоты, представляет собой отношение частоты к сумме частот.
Может выражаться в процентах:
Слайд 19
Определение. Дискретным вариационным рядом называется ранжированный в порядке возрастания или убывания
Слайд 21
Пример 1. 20 студентов на экзамене по психологии получили такие оценки
Слайд 24Накопленная (кумулятивная) частота –
какое число единиц совокупности имеет величину варианты не
где – накопленная частота варианты , – частота варианты .
Заметим, что .
Слайд 26
Если число различных значений признака (с.в. Х) в выборке велико, или
Слайд 27Если весь промежуток изменения значений выборки, от минимального до максимального, разбить
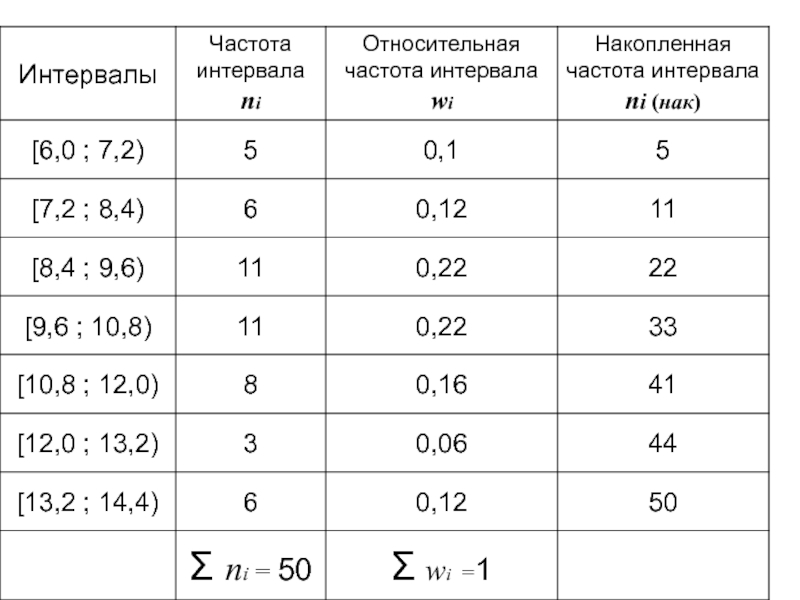
Слайд 29Пример 2. По результатам измерений получена выборка. Постройте интервальный статистический ряд
6,8
9,5 9,4 11,4 11,1 7,1 13,3 11,9 7,3 9,3 10,4
11,5 12,6 7,0 8,2 8,4 11,3 13,7 9,7 11,3 10,1
9,7 9,9 8,4 7,9 10,6 9,1 10,4 8,5 6,9 8,0
8,2 9,0 13,5 9,6 13,8 13,4 11,7 11,5 7,8 9,4
Разобьем промежуток изменения выборки на 7 интервалов и подсчитаем, сколько чисел из выборки принадлежит каждому интервалу - частоты интервалов ni
Слайд 31Вопросы:
Сколько должно быть интервалов?
Какова длина каждого интервала?
Как определить границы интервалов?
Ответ на
Слайд 33 Полигон
применяется для изображения как дискретных, так и интервальных рядов (если предварительно привести его к дискретному).
При этом по оси абсцисс откладываются варианты, а по оси ординат – частоты или частости
Слайд 38 Гистограмма
Применяется для изображения только интервальных
При этом по оси абсцисс откладываются интервалы, а по оси ординат – частоты (или частости) в случае равенства интервалов, или плотности распределения частот (или частостей) в случае неравенства интервалов.
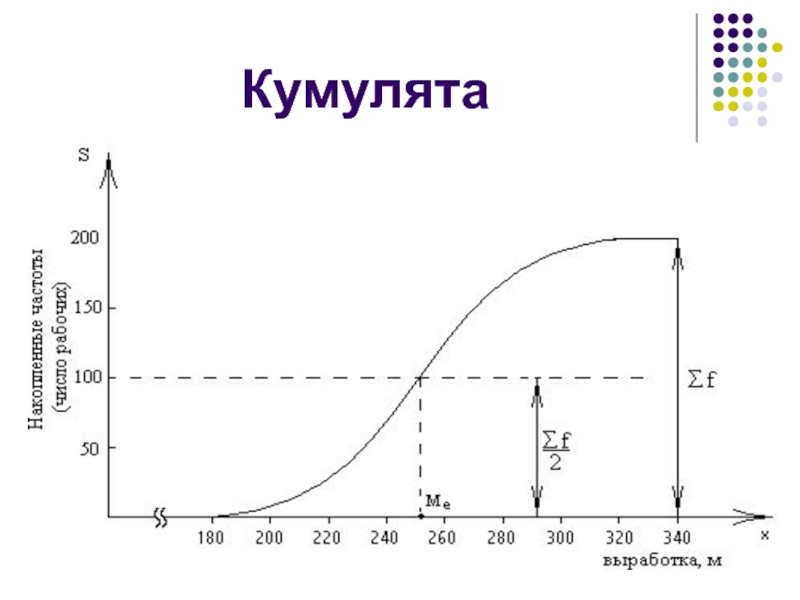
Слайд 41Кумулята
Кумулятивная кривая (кумулята) – кривая накопленных частот (частостей).
Для дискретного вариационного
или .
Слайд 42Кумулята
Для интервального вариационного ряда ломаная начинается с точки
Абсциссы других точек этой ломаной соответствуют концам интервалов, ординаты – накопленным частотам этих интервалов.
Слайд 45Средние величины
Средние величины характеризуют значение признака, вокруг которого концентрируются наблюдения или,
К ним относят: среднюю арифметическую вариационного ряда,
моду и медиану.
Слайд 46
Средней арифметической вариационного ряда называется сумма произведений всех вариантов на соответствующие
,
где xi - варианты дискретного ряда или середины интервалов интервального вариационного ряда;
ni - соответствующие им частоты; т – число неповторяющихся вариантов или число интервалов.
Слайд 48
Медиана Me - это значение, которое делит упорядоченное множество данных
Медиана может быть приближенно найдена с помощью кумуляты как значение признака, для которого
Слайд 49Показатели вариации
Дисперсией вариационного ряда называется средняя арифметическая квадратов отклонений вариантов от
Среднее квадратическое отклонение s - арифметическое значение корня квадратного из дисперсии.