- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Комбинация геометрических тел презентация
Содержание
- 1. Комбинация геометрических тел
- 3. Шар (сфера) называется вписанным в многогранник, а
- 4. Шар (сфера) называется описанным около многогранника, а
- 5. Построение чертежей пространственных фигур
- 6. Строим вместе Описанный шар около правильной треугольной
- 7. C A O1 A2
- 8. Строим вместе Правильная пирамида, вписанная в сферу
- 9. Строим вместе Сфера, вписанная в прямую призму
- 10. A2 A1 O1 B1
- 11. Строим вместе Шар, вписанный в правильную пирамиду
- 12. Задача 3. Вычислить поверхность шара, вписанного
- 13. Итог урока Выбор за вами
- 14. Совина Нина Георгиевна Спасибо за работу!
Слайд 1Тема урока:
Комбинация шара с геометрическими телами
Цели урока:
Образовательная: формировать знания, умения, навыки
Развивающая: совершенствовать навыки по решению стереометрических задач на тему: “Комбинация геометрических тел”, развивать логическое мышление, память, познавательный интерес, способствовать развитию творческой деятельности, воображения;
Воспитательная: приучать к эстетическому оформлению записи в тетради и выполнении чертежей, умению выслушивать других, прививать трудолюбие, доброжелательность, воспитывать честность в оценке своих знаний и знаний товарищей.
Слайд 2
1
1
3
5
2
4
4
6
3
2
Ответ
р
у
г
1(по вертикали):Тело, полученное вращением прямоугольного треугольника вокруг одного из его катетов.
1(по
Ответ
к
с
о
у
н
Ответ
3(по вертикали): Тело вращения, являющееся верхней частью архитектурного сооружения.
к
у
л
п
о
2(по горизонтали): Прямая, при вращении которой вокруг оси образуется боковая поверхность цилиндра, конуса.
Ответ
б
р
з
я
а
щ
ю
а
Ответ
2(по вертикали): Плоская фигура, при вращении которой образуется усеченный конус.
т
а
п
е
ц
и
я
Ответ
5: Тело, полученное вращением полукруга вокруг его диаметра.
р
ш
Ответ
4(по вертикали): Отрезок, соединяющий две точки сферы и проходящий через центр шара
и
д
м
а
т
е
р
3(по горизонтали): Тело, полученное вращением прямоугольника вокруг одной из его сторон.
Ответ
д
н
и
р
л
4(по горизонтали): Угол между высотой и плоскостью основания конуса.
Ответ
п
р
й
о
я
м
Ответ
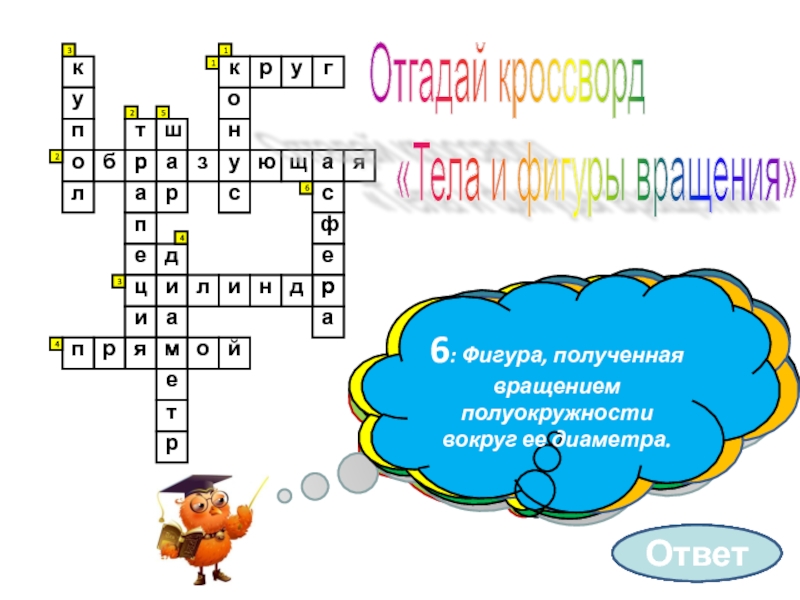
6: Фигура, полученная вращением полуокружности вокруг ее диаметра.
с
ф
е
а
р
р
Отгадай кроссворд
«Тела и фигуры вращения»
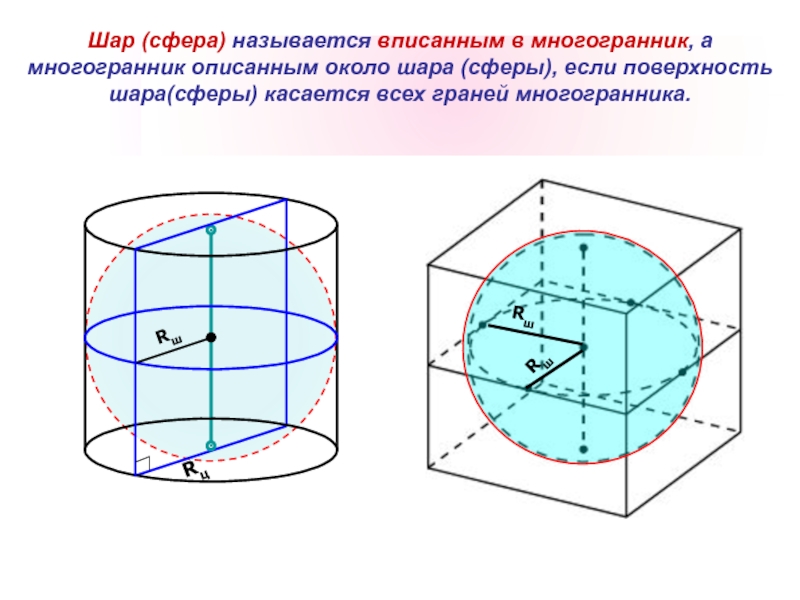
Слайд 3Шар (сфера) называется вписанным в многогранник, а многогранник описанным около шара
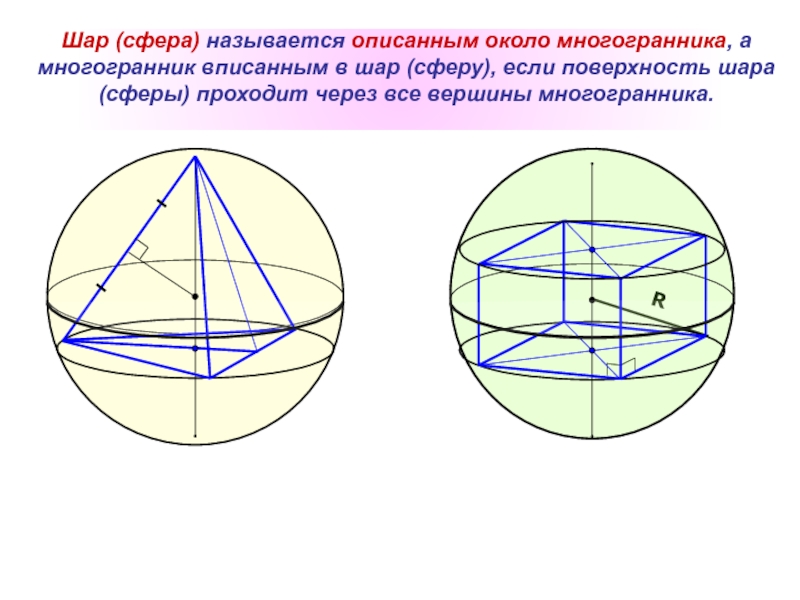
Слайд 4Шар (сфера) называется описанным около многогранника, а многогранник вписанным в шар
R
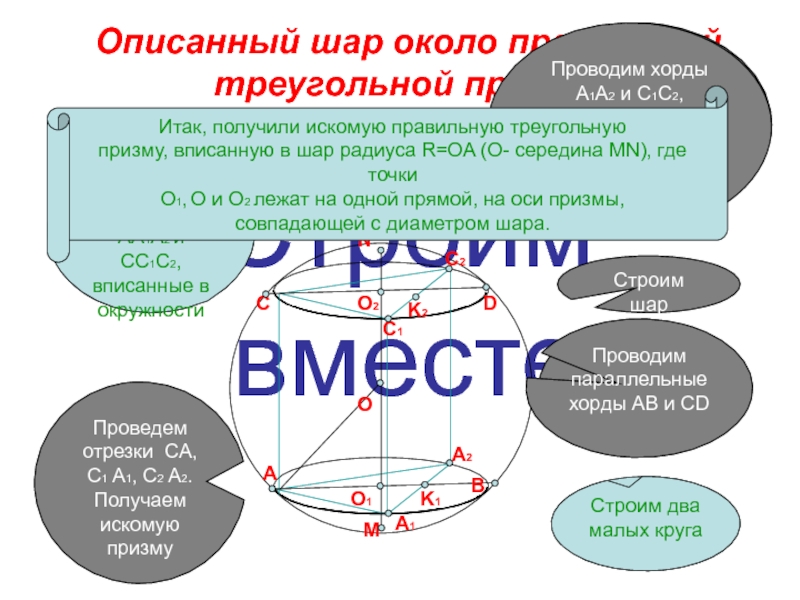
Слайд 6Строим вместе
Описанный шар около правильной треугольной призмы
Строим два малых
Получаем треугольники АA1A2 и СC1C2, вписанные в окружности
C
A
O1
A2
M
B
K1
A1
O2
N
C2
C1
K2
D
O
Проведем отрезки CA, C1 A1, С2 A2. Получаем искомую призму
Проводим параллельные хорды АВ и СD
Строим шар
Проводим хорды A1A2 и C1C2, которые перпендикулярны AB и CD и делят О1В и О2D пополам
Итак, получили искомую правильную треугольную
призму, вписанную в шар радиуса R=OA (О- середина MN), где точки
O1, O и O2 лежат на одной прямой, на оси призмы,
совпадающей с диаметром шара.
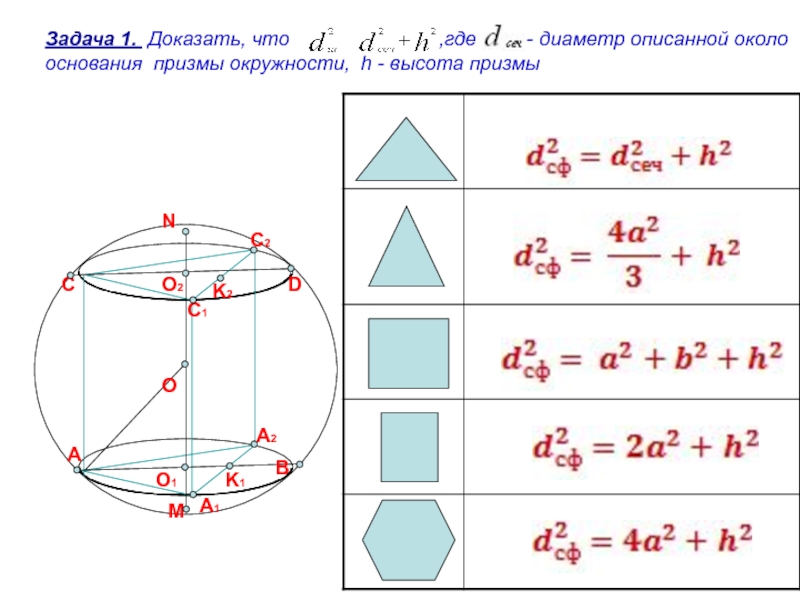
Слайд 7
C
A
O1
A2
M
B
K1
A1
O2
N
C2
C1
K2
D
O
Задача 1. Доказать, что
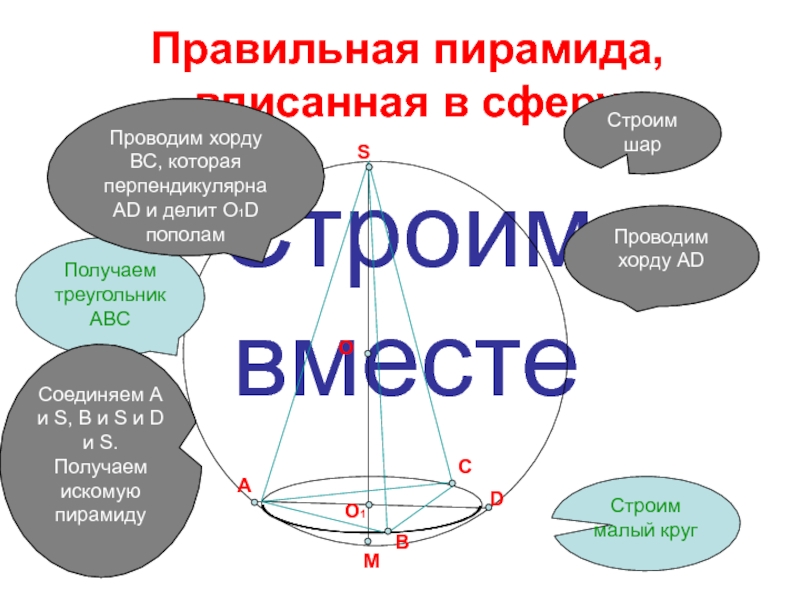
Слайд 8Строим вместе
Правильная пирамида, вписанная в сферу
O
A
D
C
B
O1
S
M
Строим малый круг
Получаем треугольник ABC
Проводим хорду
Строим шар
Проводим хорду ВС, которая перпендикулярна АD и делит О1D пополам
Соединяем A и S, B и S и D и S. Получаем искомую пирамиду
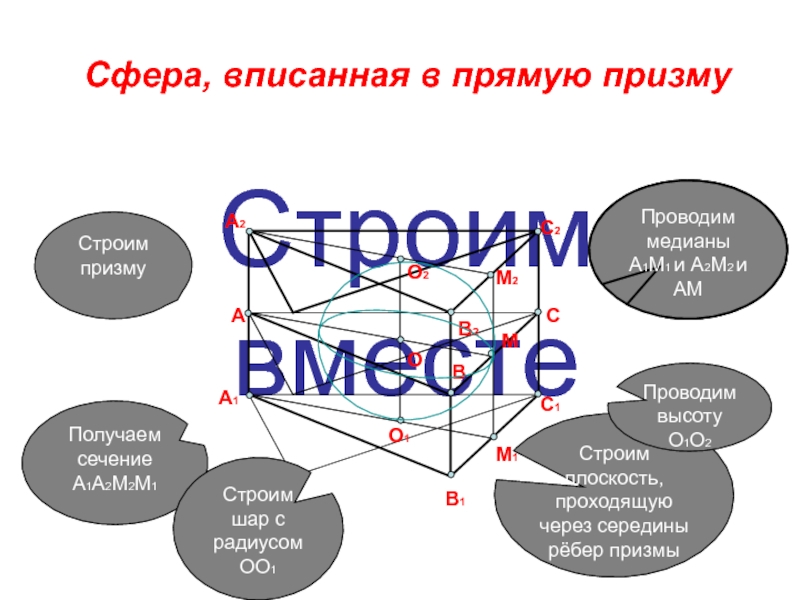
Слайд 9Строим вместе
Сфера, вписанная в прямую призму
A2
A1
O1
B1
M1
C1
C2
O2
O
B2
B
A
C
M2
Строим призму
Проводим медианы А1М1 и А2М2
Получаем сечение A1A2M2M1
Строим плоскость, проходящую через середины рёбер призмы
M
Строим шар с радиусом OO1
Проводим высоту O1O2
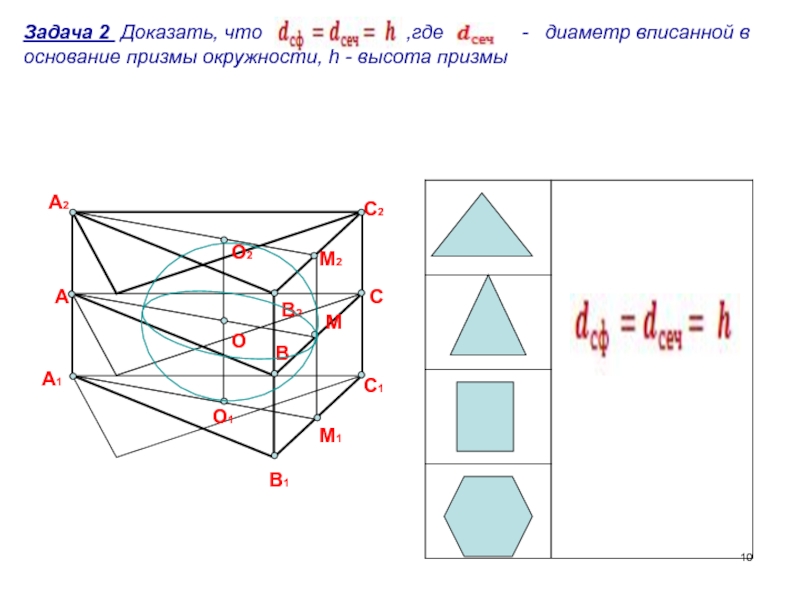
Слайд 10
A2
A1
O1
B1
M1
C1
C2
O2
O
B2
B
A
C
M2
M
Задача 2 Доказать, что ,где - диаметр вписанной в основание призмы окружности, h - высота призмы
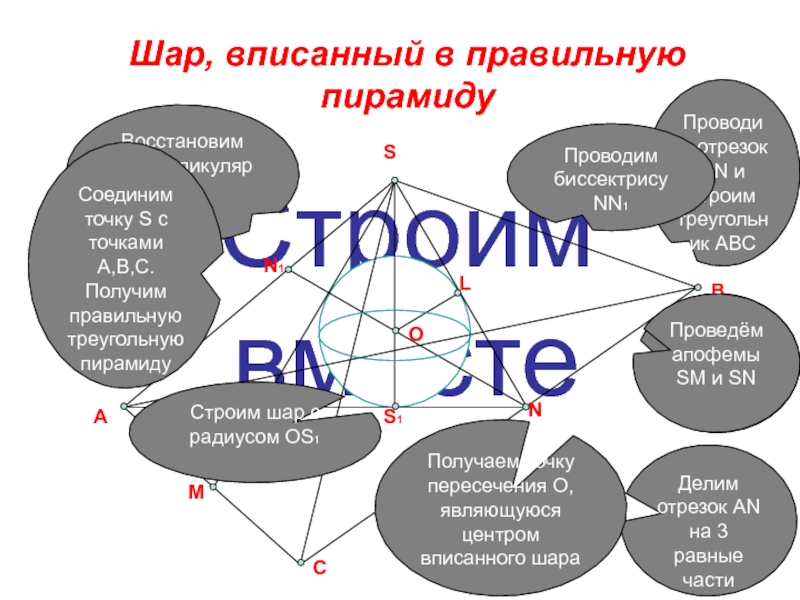
Слайд 11Строим вместе
Шар, вписанный в правильную пирамиду
A
C
B
O
S
N
M
N1
L
S1
Проводим отрезок AN и строим треугольник
Делим отрезок AN на 3 равные части
Восстановим перпендикуляр SS1
Соединим точку S с точками A,B,C. Получим правильную треугольную пирамиду
Проведём апофемы SM и SN
Проводим биссектрису NN1
Получаем точку пересечения O, являющуюся центром вписанного шара
Строим шар с радиусом OS1
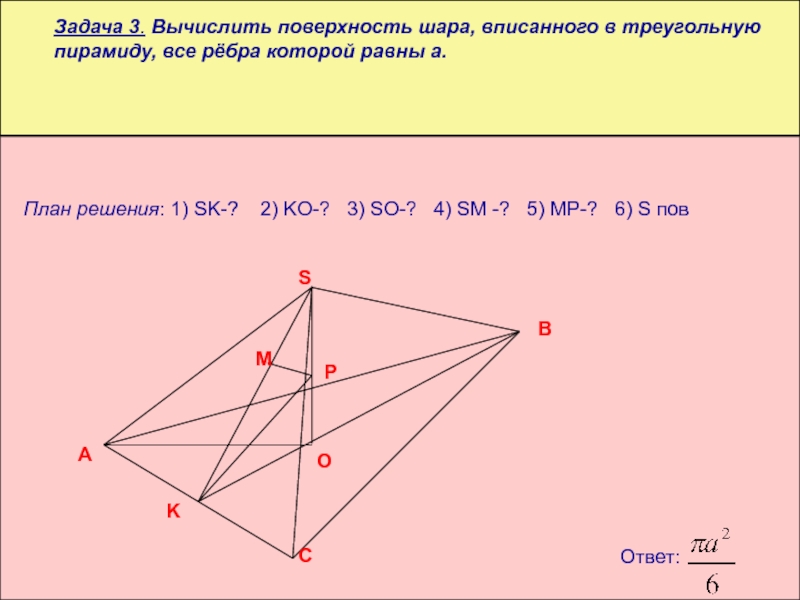
Слайд 12
Задача 3. Вычислить поверхность шара, вписанного в треугольную пирамиду, все рёбра
С
M
S
B
P
A
K
О
Ответ:
План решения: 1) SK-? 2) KO-? 3) SO-? 4) SM -? 5) MP-? 6) S пов
Слайд 13Итог урока
Выбор за вами
Я ничего не понял и
с нетерпением ждал
На уроке было
не интересно
Я все понял.
Урок понравился