развития» г. Радужный
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Правильные многоугольники презентация
Содержание
- 1. Правильные многоугольники
- 2. Выпуклый многоугольник Многоугольник называется
- 3. Правильный многоугольник Правильный треугольник Квадрат
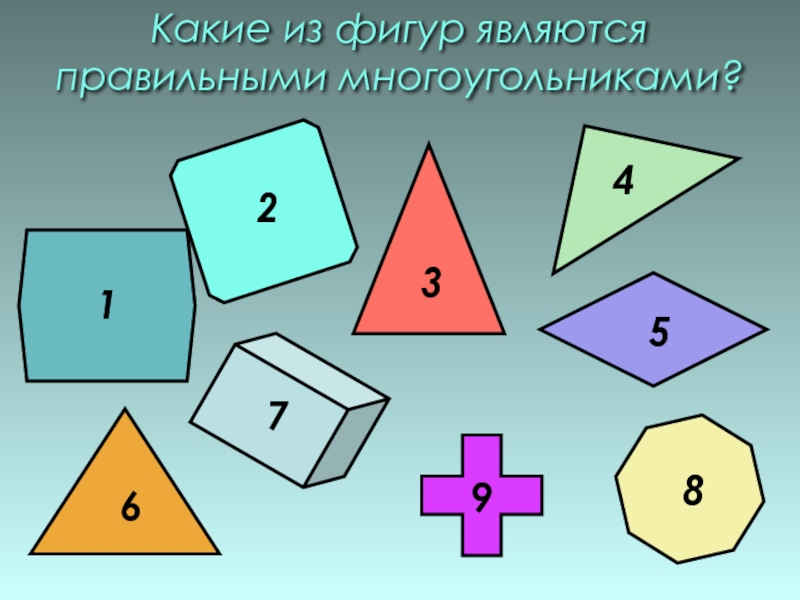
- 4. Какие из фигур являются правильными многоугольниками?
- 5. Сумма углов выпуклого n –
- 6. Вписанная окружность Если все
- 7. Описанная окружность Если все вершины
- 8. Теорема об окружности, описанной около правильного многоугольника
- 9. Теорема об окружности, вписанной в правильный многоугольник
- 10. О R r
Выпуклый многоугольник Многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины.
Слайд 1Учитель математики: Семёнова Елена Юрьевна
Правильные многоугольники
МБОУ СОШ №5 «Школа здоровья и
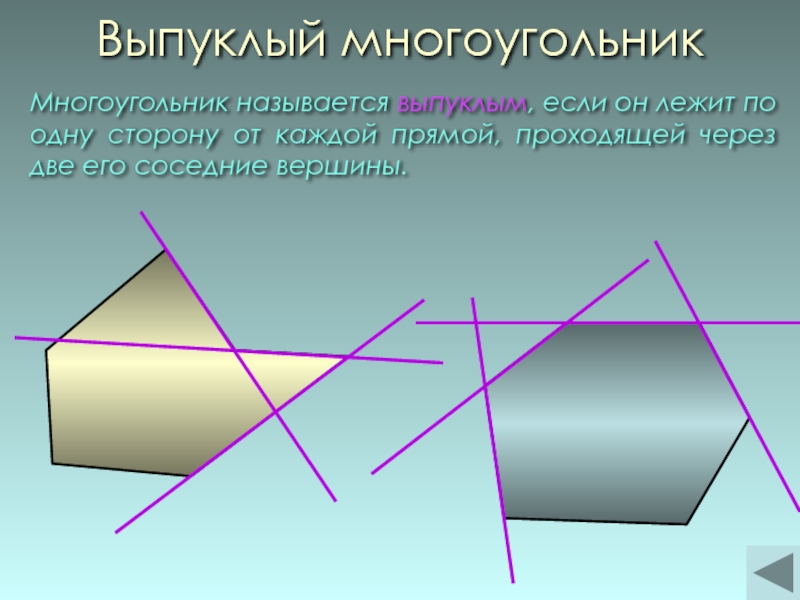
Слайд 2Выпуклый многоугольник
Многоугольник называется выпуклым, если он лежит по одну сторону от
каждой прямой, проходящей через две его соседние вершины.
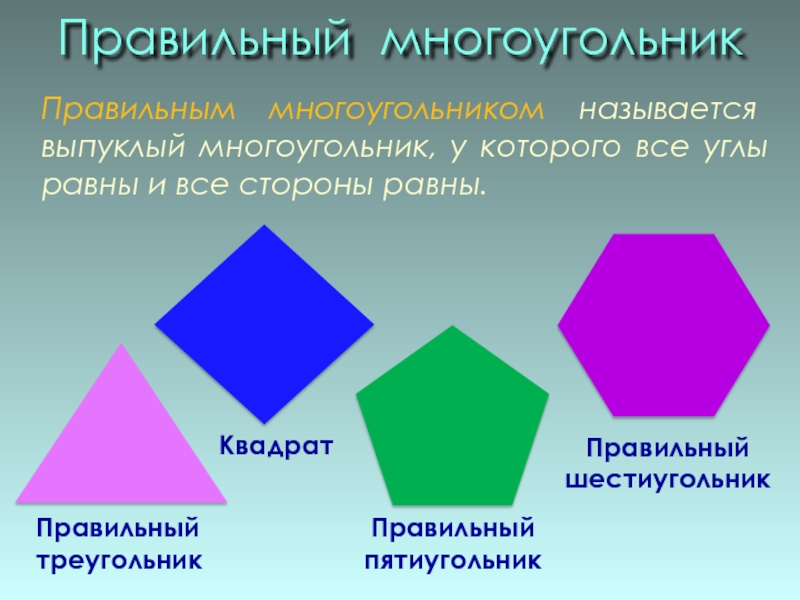
Слайд 3Правильный многоугольник
Правильный
треугольник
Квадрат
Правильный
пятиугольник
Правильный
шестиугольник
Правильным многоугольником называется выпуклый многоугольник, у которого
все углы равны и все стороны равны.
Слайд 5
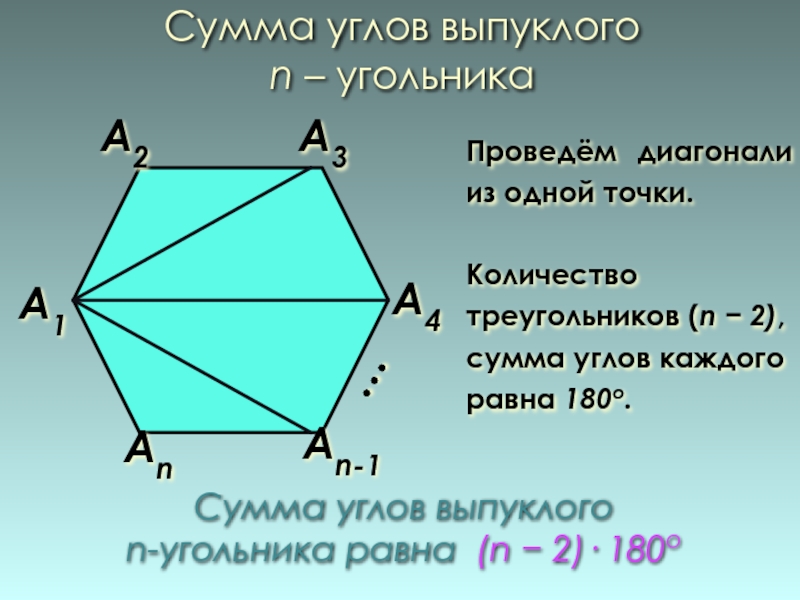
Сумма углов выпуклого
n – угольника
А1
Аn
А4
А3
А2
Проведём диагонали из одной точки.
Количество
треугольников (n − 2), сумма углов каждого равна 180о.
Сумма углов выпуклого
n-угольника равна (n − 2)· 180о
Аn-1
…
Слайд 6
Вписанная окружность
Если все стороны многоугольника касаются окружности, то окружность называется
вписанной в многоугольник, а многоугольник – описанным около этой окружности.
О
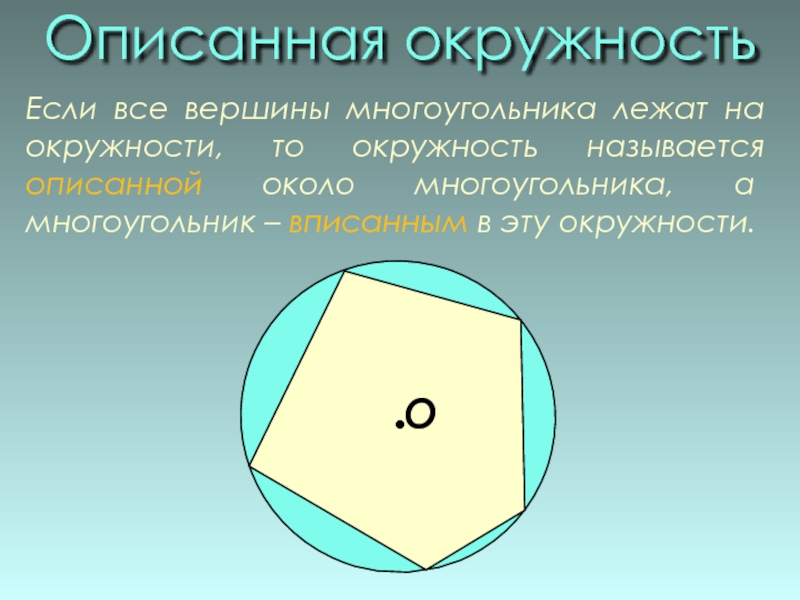
Слайд 7Описанная окружность
Если все вершины многоугольника лежат на окружности, то окружность
называется описанной около многоугольника, а многоугольник – вписанным в эту окружности.
О
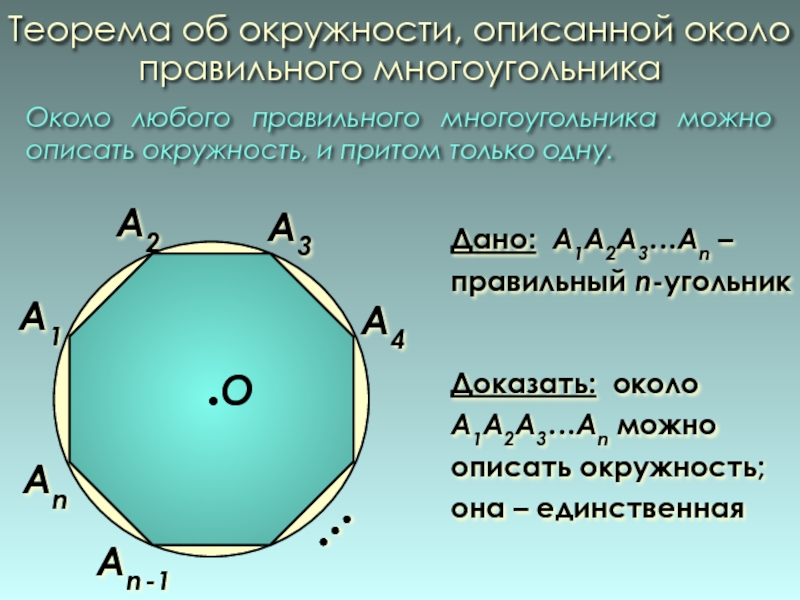
Слайд 8Теорема об окружности, описанной около правильного многоугольника
А1
Аn -1
А3
А2
Аn
…
А4
Дано: А1А2А3…Аn – правильный
n-угольник
Доказать: около А1А2А3…Аn можно описать окружность; она – единственная
Около любого правильного многоугольника можно описать окружность, и притом только одну.
О
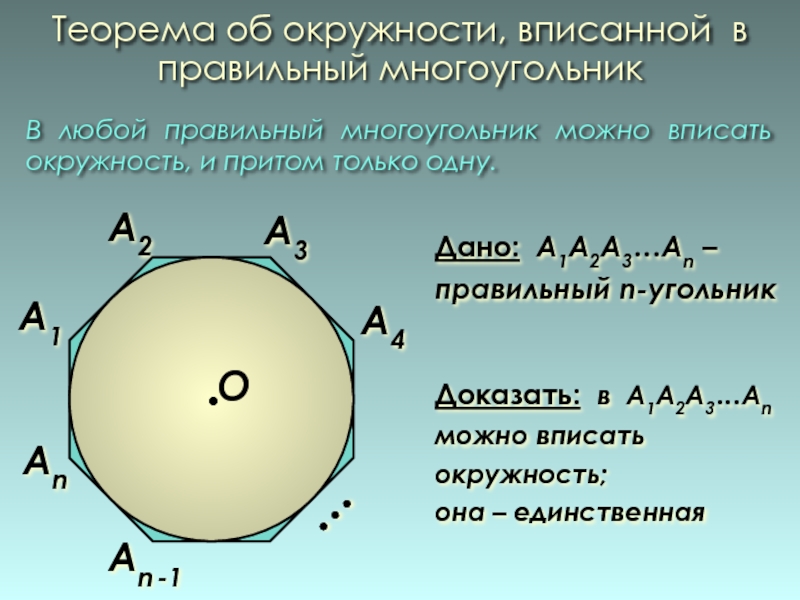
Слайд 9Теорема об окружности, вписанной в правильный многоугольник
А2
А1
Аn -1
А3
Аn
…
А4
В любой правильный многоугольник
можно вписать окружность, и притом только одну.
Дано: А1А2А3…Аn – правильный n-угольник
Доказать: в А1А2А3…Аn можно вписать окружность;
она – единственная
О
Слайд 10
О
R
r
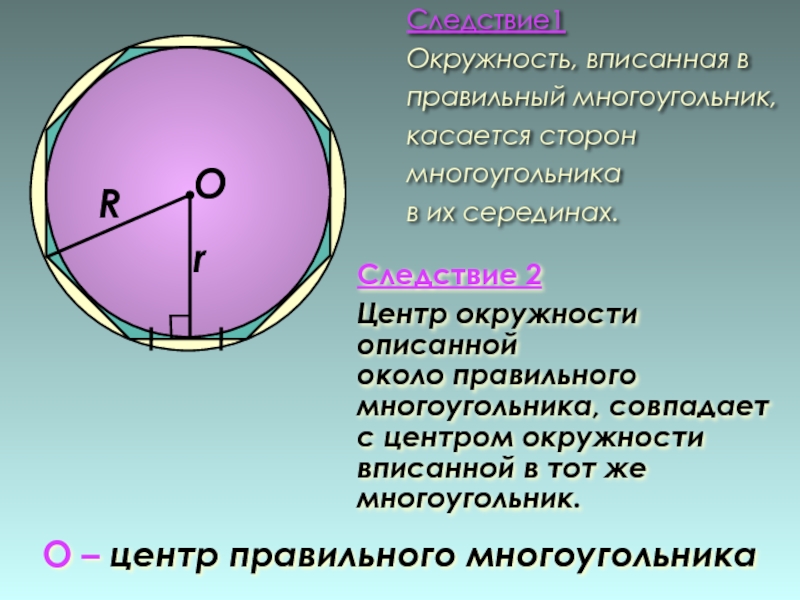
Следствие 2
Центр окружности описанной
около правильного
многоугольника, совпадает с центром окружности
вписанной в
тот же
многоугольник.
многоугольник.
Следствие1
Окружность, вписанная в правильный многоугольник,
касается сторон
многоугольника
в их серединах.
О – центр правильного многоугольника
