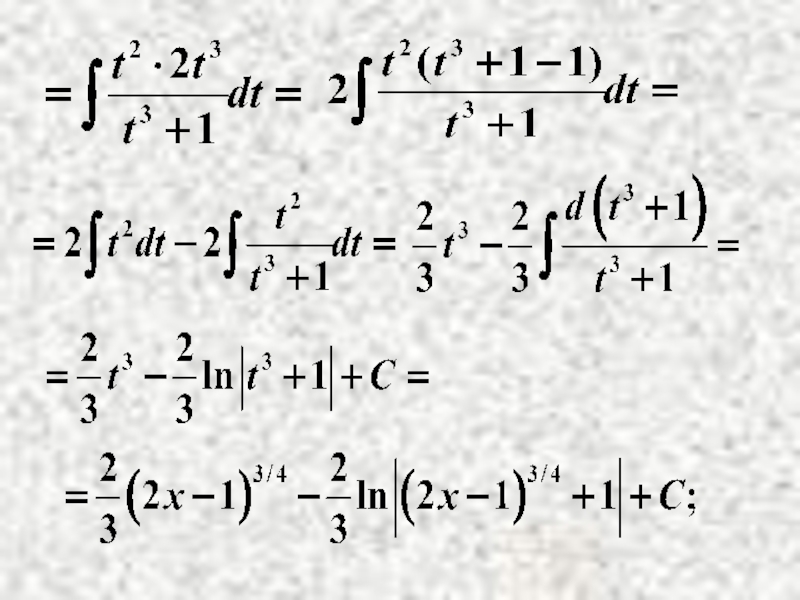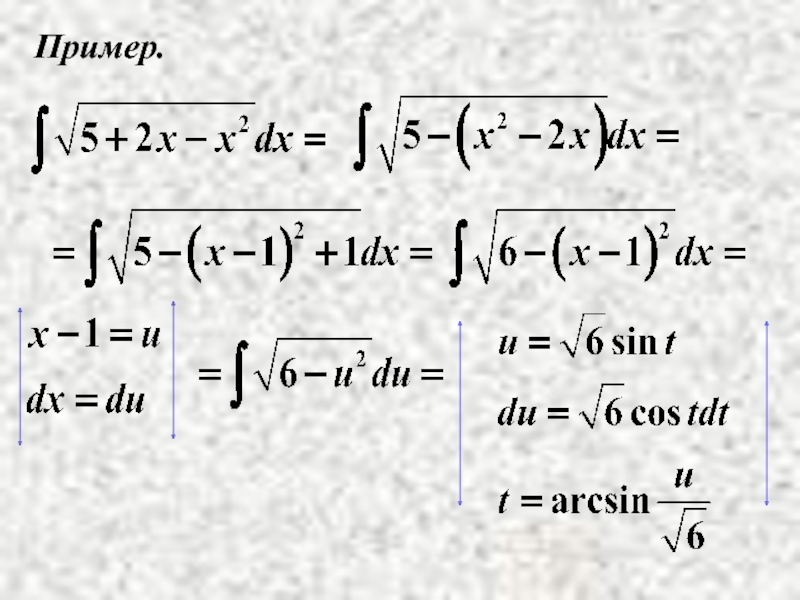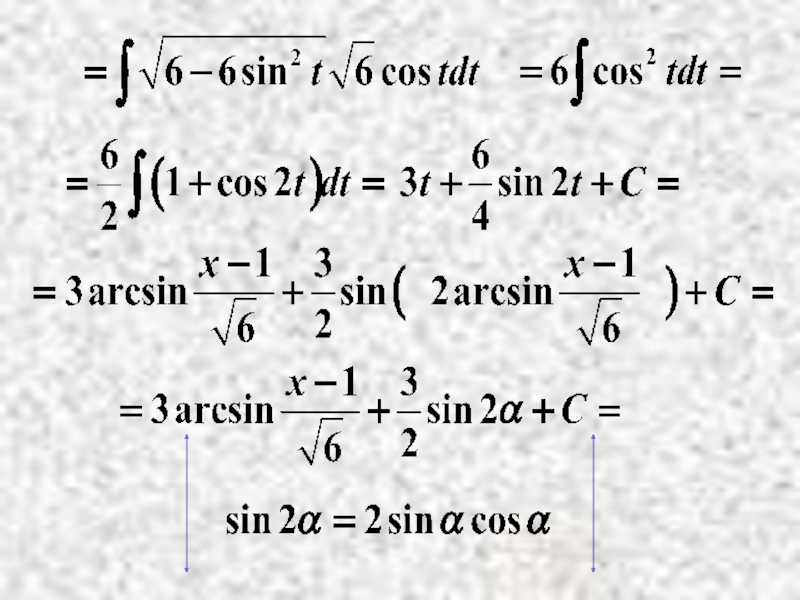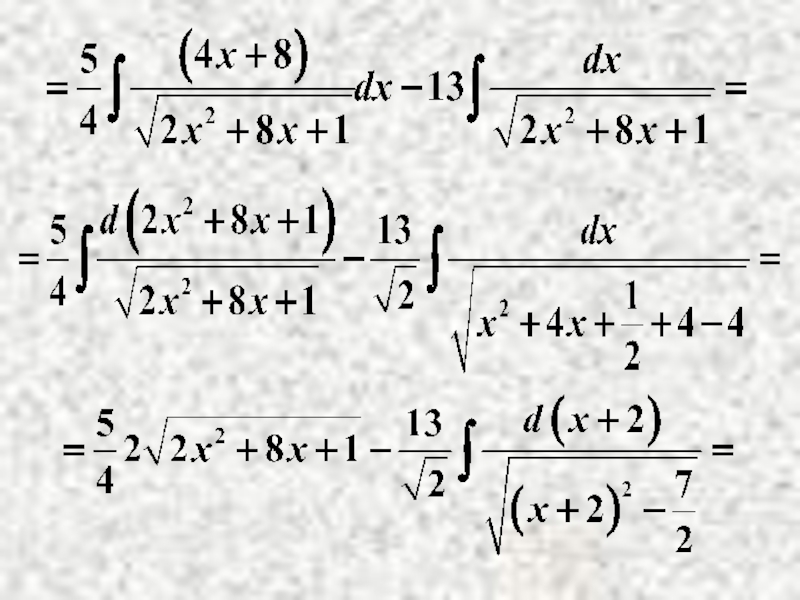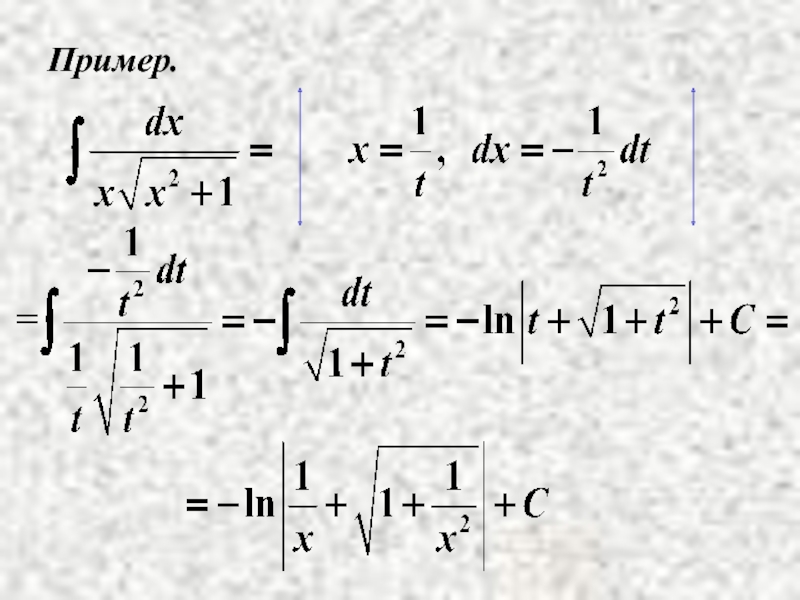- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Классы интегрируемых функций. Интегрирование иррациональных выражений презентация
Содержание
- 1. Классы интегрируемых функций. Интегрирование иррациональных выражений
- 2. Лекция 7 Классы интегрируемых функций. Интегрирование иррациональных выражений. I. Линейные иррациональности.
- 3. - линейная иррациональность, дробно-рациональная функция
- 4. В результате интеграл
- 6. II. Дробно-линейные иррациональности. - дробно-линейная иррациональность. Пусть S – общий знаменатель дробей
- 7. После подстановки указанный интеграл сводится
- 8. III. Квадратичные иррациональности. Тригонометрические подстановки. - квадратичная иррациональность, дробно-рациональная функция двух аргументов.
- 9. Метод. После выделения полного квадрата в квадратном
- 10. После такой замены интеграл сводится к интегралу от тригонометрических функций:
- 11. Пример.
- 14. Частные случаи квадратичных
- 15. В числителе выделяется производная квадратного трехчлена, стоящего в знаменателе. Пример.
- 18. Пример.
Лекция 7 Классы интегрируемых функций. Интегрирование иррациональных выражений. I. Линейные иррациональности.
Слайд 2
Лекция 7
Классы интегрируемых функций.
Интегрирование иррациональных
выражений.
I. Линейные иррациональности.
Слайд 3- линейная иррациональность,
дробно-рациональная функция
своих аргументов.
Метод.
Если S – общий
знаменатель дробей
то используется подстановка:
то используется подстановка:
Слайд 4
В результате интеграл сводится к интегралу
от дробно-рациональной функции
аргумента t.
Пример.
Слайд 6II. Дробно-линейные иррациональности.
- дробно-линейная иррациональность.
Пусть S – общий знаменатель дробей
Слайд 7После подстановки
указанный интеграл сводится к интегралу
от дробно-рациональной функции
аргумента t
(корни исчезают).
(корни исчезают).
Слайд 8III. Квадратичные иррациональности.
Тригонометрические подстановки.
- квадратичная иррациональность,
дробно-рациональная функция двух
аргументов.
Слайд 9Метод.
После выделения полного квадрата в квадратном
трёхчлене
и замены
интеграл сводится к одному из трёх типов:
Слайд 14
Частные случаи квадратичных
иррациональностей.
Выделением полного квадрата в
знаменателе
интеграл сводится к табличному.
интеграл сводится к табличному.
Пример.
