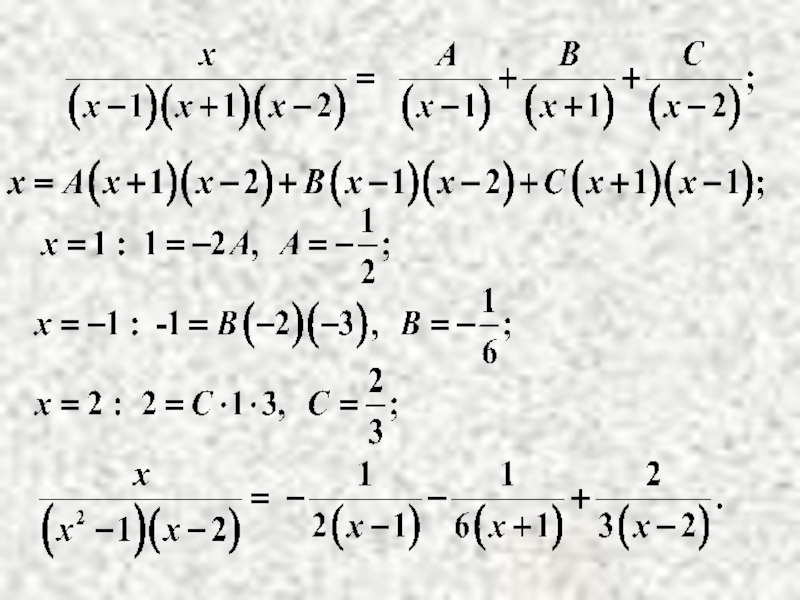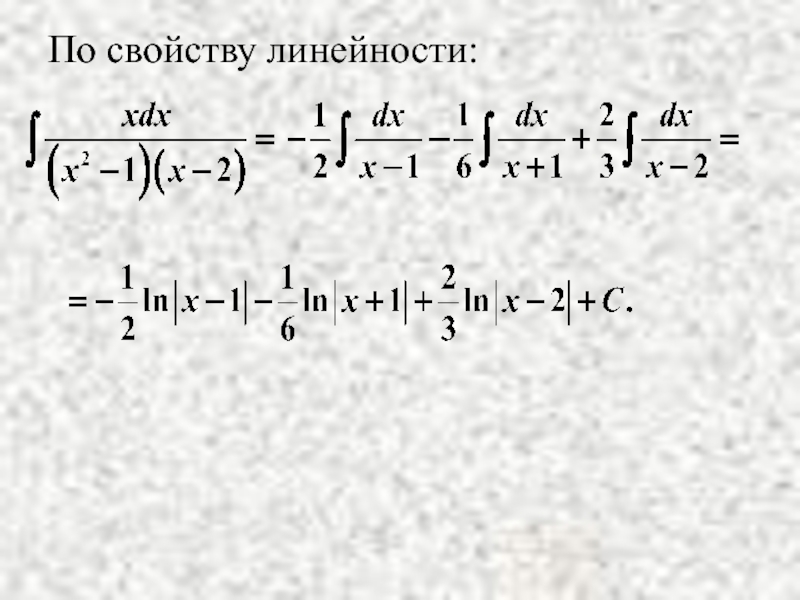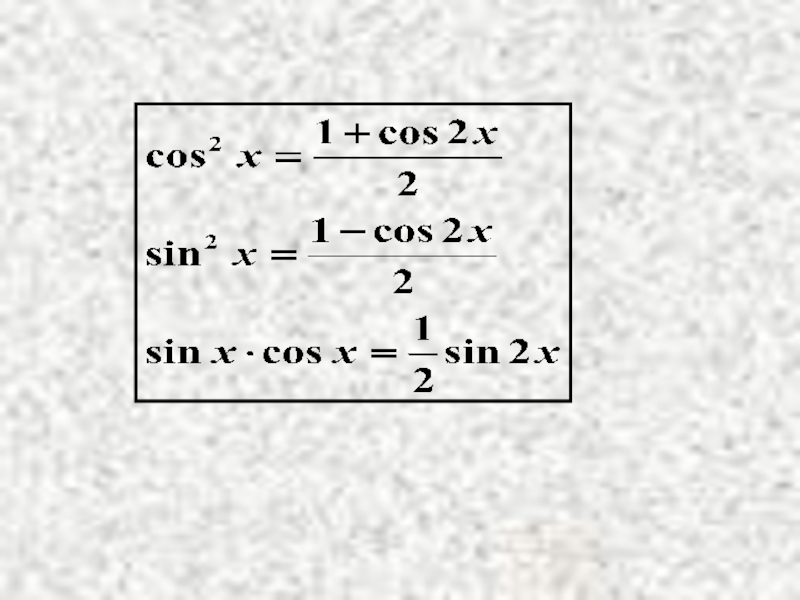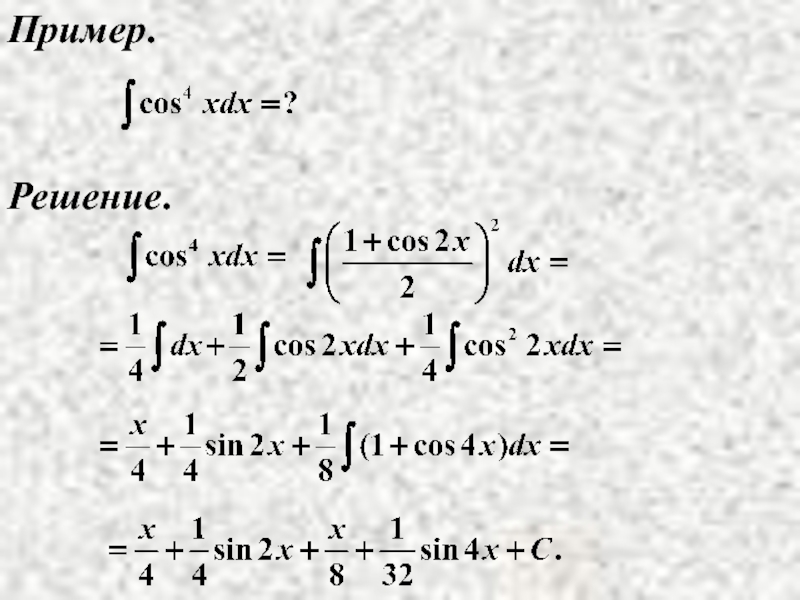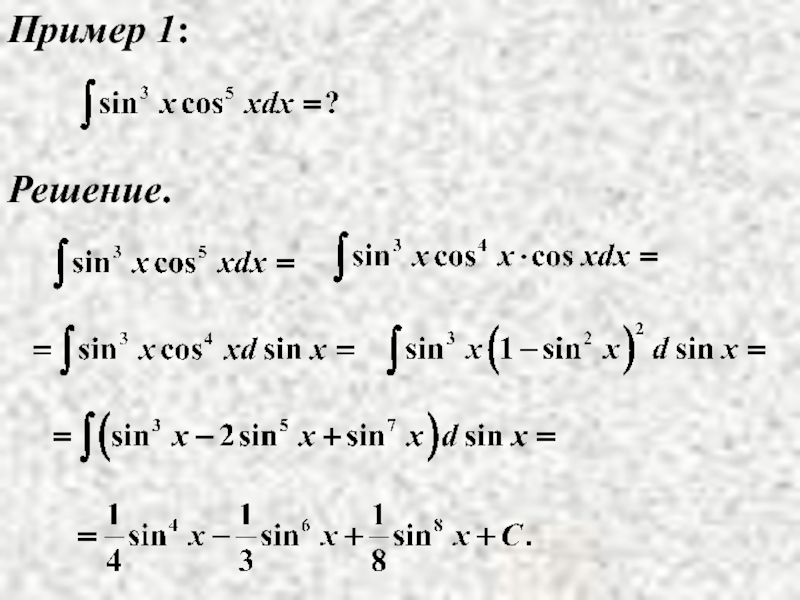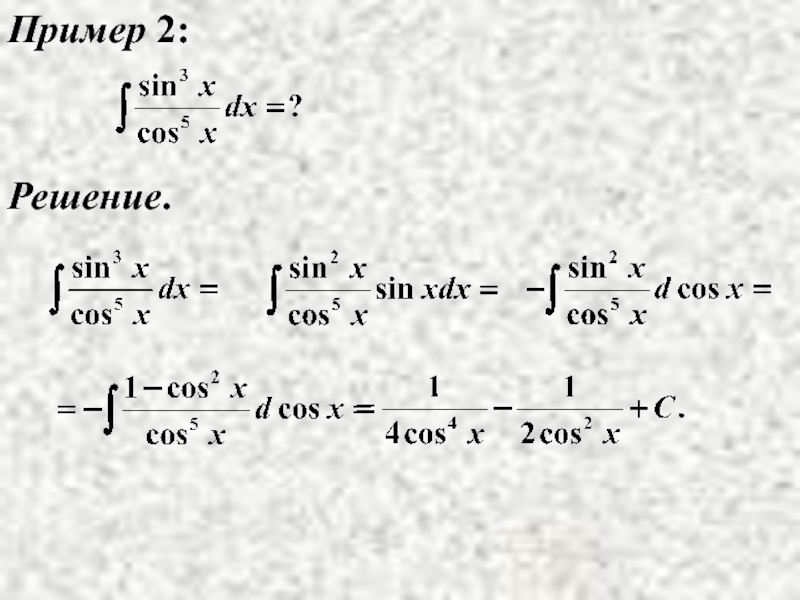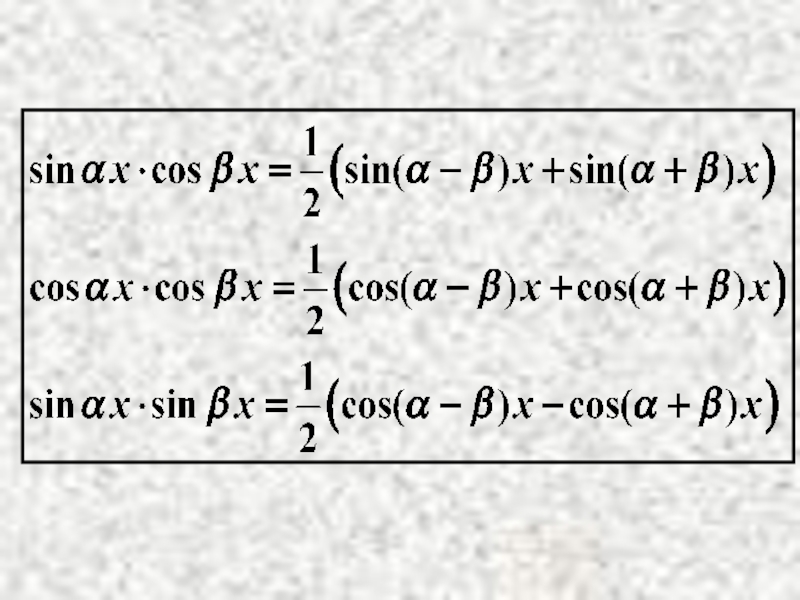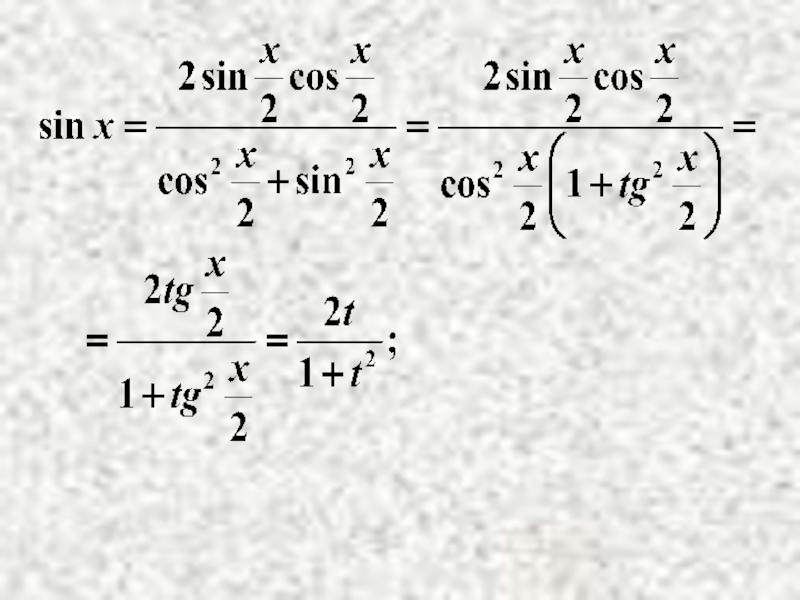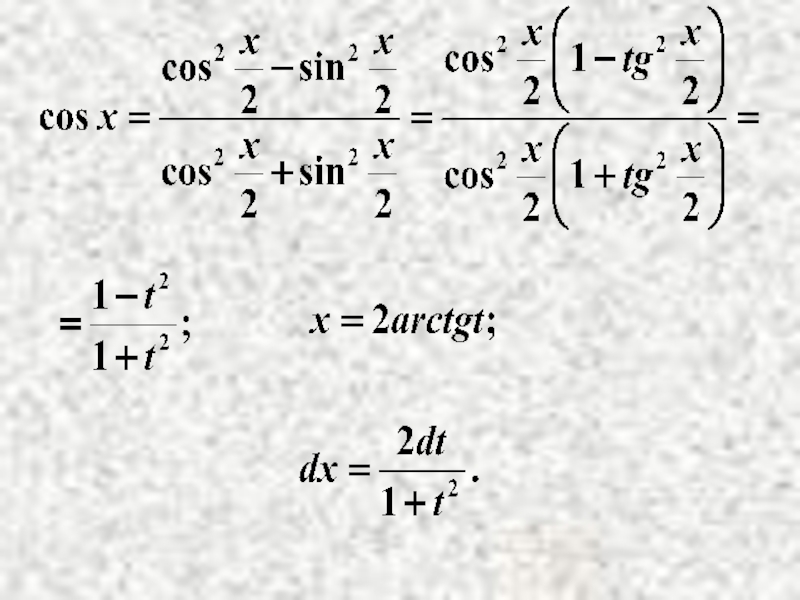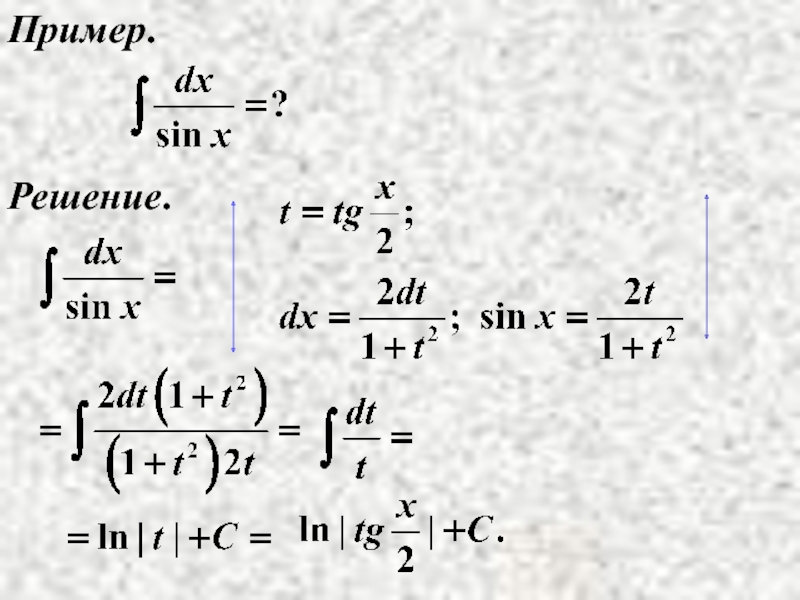- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Классы интегрируемых функций презентация
Содержание
- 1. Классы интегрируемых функций
- 3. 4) Интегрируют каждую простейшую дробь.
- 4. Правильную рациональную дробь можно разложить на сумму простейших дробей четырех типов:
- 5. Коэффициенты Ai,Mi,Ni могут быть найдены после приведения суммы простейших дробей к общему знаменателю.
- 6. Пример. Разлагаем правильную дробь на сумму простейших дробей:
- 8. По свойству линейности:
- 9. Интегрирование выражений, содержащих тригонометрические функции. а)
- 11. Пример. Решение.
- 12. б) хотя бы одно из n и
- 13. Пример 1: Решение.
- 14. Пример 2: Решение.
- 15. Метод: переход к сумме функций и сумме
- 17. Метод - универсальная тригонометрическая подстановка: рациональная функция. Здесь
- 20. Окончательно: (Интеграл приводится к интегралу от рациональной дроби).
- 21. Пример. Решение.
- 22. Замечание. Если подынтегральная функция R(sinx,cosx) является чётной
Слайд 1
Лекция 6
Классы интегрируемых функций
Интегрирование рациональных дробей.
Интегрирование выражений, содержащих тригонометрические функции.
1)
2)
Слайд 5 Коэффициенты Ai,Mi,Ni могут быть найдены после приведения суммы простейших дробей
Слайд 9Интегрирование выражений, содержащих
тригонометрические функции.
а) n и m – чётные, целые,
Метод: понижение степени переходом к
двойному аргументу с помощью формул
тригонометрии:
Слайд 12б) хотя бы одно из n и m - нечётное, целое,
Метод:от нечётной степени отделяется один сомножитель и заносится под знак дифференциала;
оставшаяся подынтегральная функция выражается через
функцию, стоящую под знаком дифференциала при помощи формулы
Слайд 15Метод: переход к сумме функций и сумме
При этом используются следующие тригонометрические формулы:
Слайд 22Замечание.
Если подынтегральная функция R(sinx,cosx) является чётной функцией аргументов sinx и cosx,
Пример.