- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Классификация игр презентация
Содержание
- 1. Классификация игр
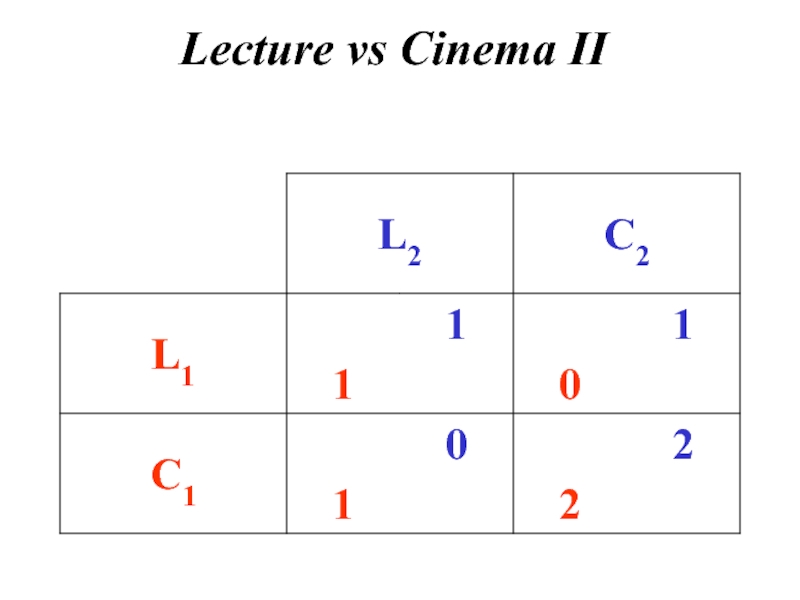
- 2. Lecture vs Cinema II
- 3. Слабое доминирование стратегий ⊐ G = {I
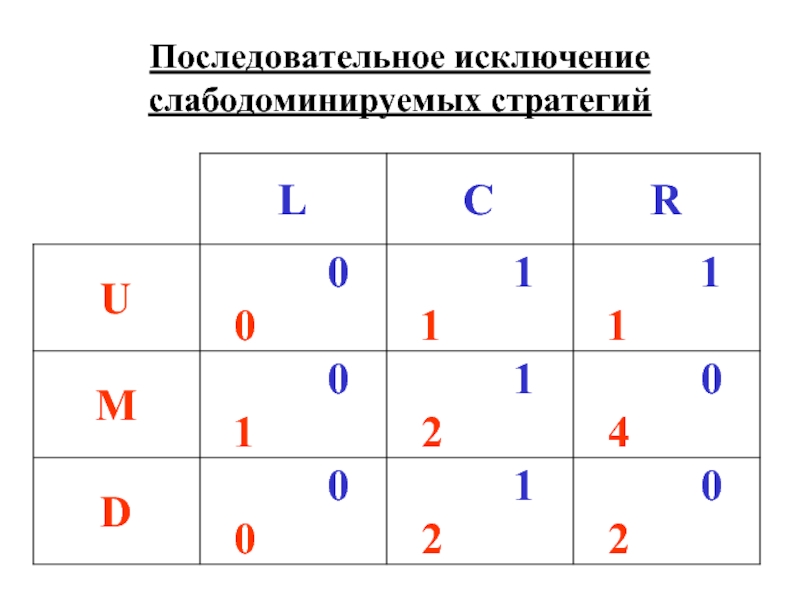
- 4. Последовательное исключение слабодоминируемых стратегий
- 5. Наилучшие отклики (best responses) ⊐ G =
- 6. Никогда не лучшие отклики (never a best
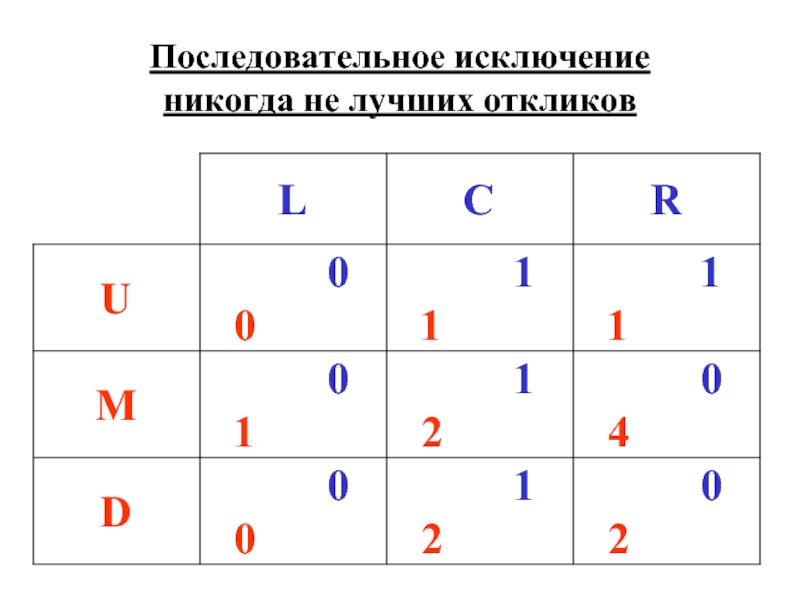
- 7. Последовательное исключение никогда не лучших откликов
- 8. Различные решения задач теории игр
- 9. Равновесие по Нэшу как набор наилучших откликов
- 10. Равновесие по Нэшу (Nash equilibrium) ⊐ G
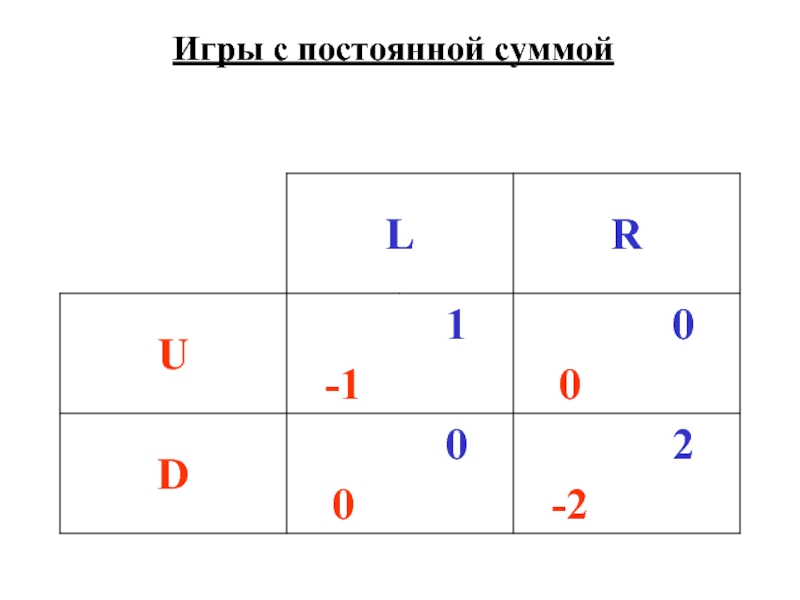
- 11. Игры с постоянной суммой
Слайд 1Классификация игр
некооперативные/кооперативные
статические/динамические
с полной информацией/с неполной информацией
Слайд 3Слабое доминирование стратегий
⊐ G = {I ; S ; U}, i
∈ I.
Стратегия s'i слабо доминирует стратегию s''i игрока i, если
ui (s'i , s–i) ≥ ui (s''i , s–i) для ∀s–i ∈ S–i и
∃ŝ–i ∈ S–i : ui (s'i , ŝ–i) > ui (s''i , ŝ–i) .
Обозначение
s'i ≻ s''i
Стратегия s'i слабо доминирует стратегию s''i игрока i, если
ui (s'i , s–i) ≥ ui (s''i , s–i) для ∀s–i ∈ S–i и
∃ŝ–i ∈ S–i : ui (s'i , ŝ–i) > ui (s''i , ŝ–i) .
Обозначение
s'i ≻ s''i
Слайд 5Наилучшие отклики
(best responses)
⊐ G = {I ; S ; U}; i
∈ I ; ŝ–i ∈ S–i.
Стратегия s'i является наилучшим откликом игрока i на ŝ–i , если
ui (s'i , ŝ–i) ≥ ui (s''i , ŝ–i) для ∀ s''i ∈ Si.
Обозначение
s'i ∈ bi(ŝ–i)
Стратегия s'i является наилучшим откликом игрока i на ŝ–i , если
ui (s'i , ŝ–i) ≥ ui (s''i , ŝ–i) для ∀ s''i ∈ Si.
Обозначение
s'i ∈ bi(ŝ–i)
Слайд 6Никогда не лучшие отклики
(never a best responses)
⊐ G = {I ;
S ; U}; i ∈ I ; s'i ∈ Si.
Стратегия s'i является никогда не лучшим откликом игрока i, если
∄ ŝ–i ∈ S–i , что s'i ∈ bi(ŝ–i).
Стратегия s'i является никогда не лучшим откликом игрока i, если
∄ ŝ–i ∈ S–i , что s'i ∈ bi(ŝ–i).
Слайд 9Равновесие по Нэшу
как набор наилучших откликов
⊐ G = {I ; S
; U};
s∗ = (s∗1 , s∗2 , … , s∗n) ∈ S.
Набор стратегий s∗ является равновесием по Нэшу игры G, если
для ∀ i ∈ I
s∗i ∈ bi(s∗–i).
s∗ = (s∗1 , s∗2 , … , s∗n) ∈ S.
Набор стратегий s∗ является равновесием по Нэшу игры G, если
для ∀ i ∈ I
s∗i ∈ bi(s∗–i).
Слайд 10Равновесие по Нэшу
(Nash equilibrium)
⊐ G = {I ; S ; U};
s∗ = (s∗1 , s∗2 , … , s∗n) ∈ S.
Набор стратегий s∗ является равновесием по Нэшу игры G, если
для ∀ i ∈ I
ui (s∗i , s∗–i) ≥ ui (si , s∗–i) для ∀ si ∈ Si.
Обозначение
s∗ ∈ NE(G)
Набор стратегий s∗ является равновесием по Нэшу игры G, если
для ∀ i ∈ I
ui (s∗i , s∗–i) ≥ ui (si , s∗–i) для ∀ si ∈ Si.
Обозначение
s∗ ∈ NE(G)