- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Сечения призмы презентация
Содержание
- 1. Сечения призмы
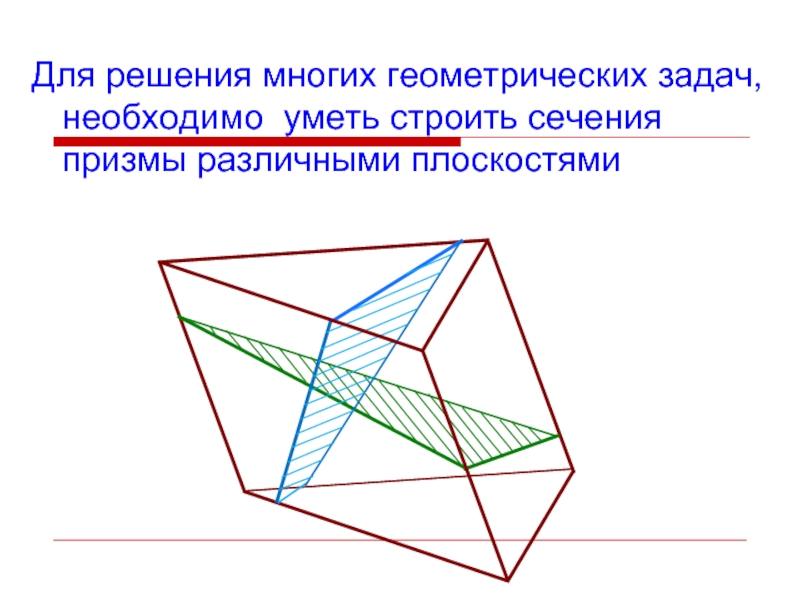
- 2. Для решения многих геометрических задач, необходимо уметь строить сечения призмы различными плоскостями
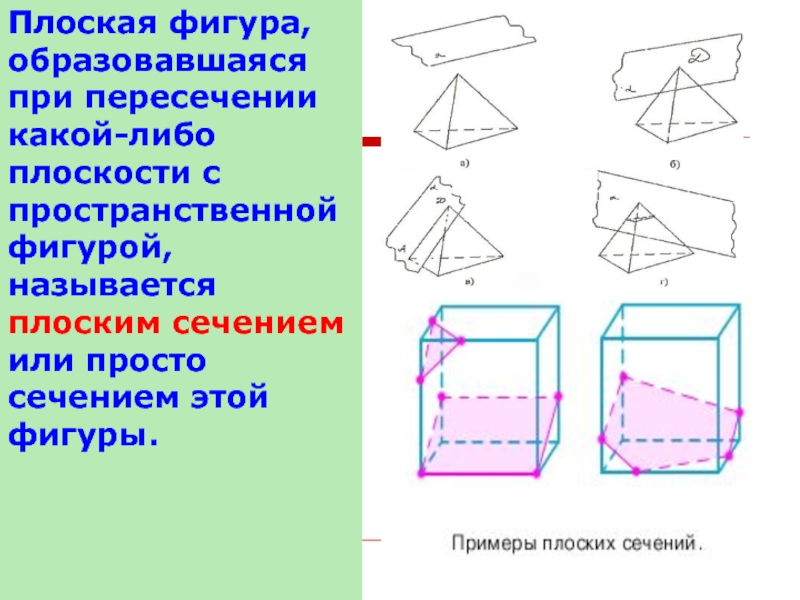
- 3. Плоская фигура, образовавшаяся при пересечении какой-либо плоскости
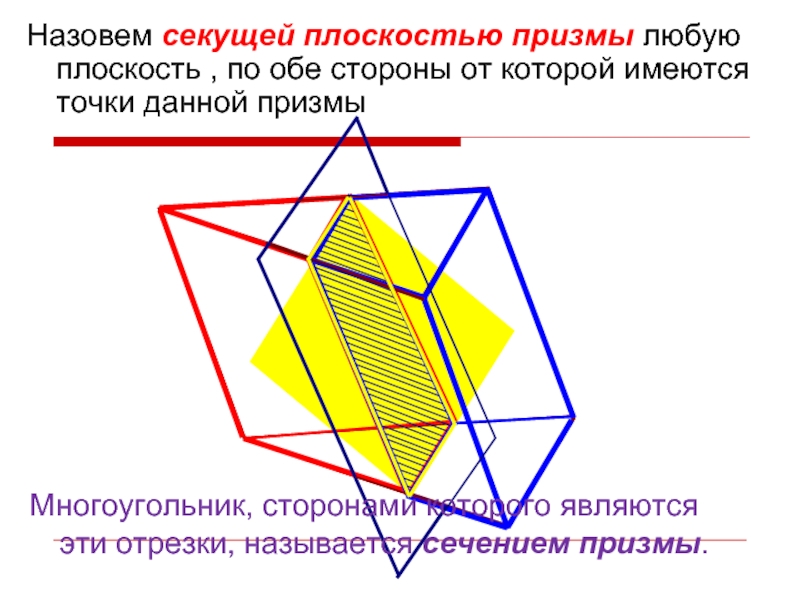
- 4. Назовем секущей плоскостью призмы любую плоскость
- 5. Сечением призмы
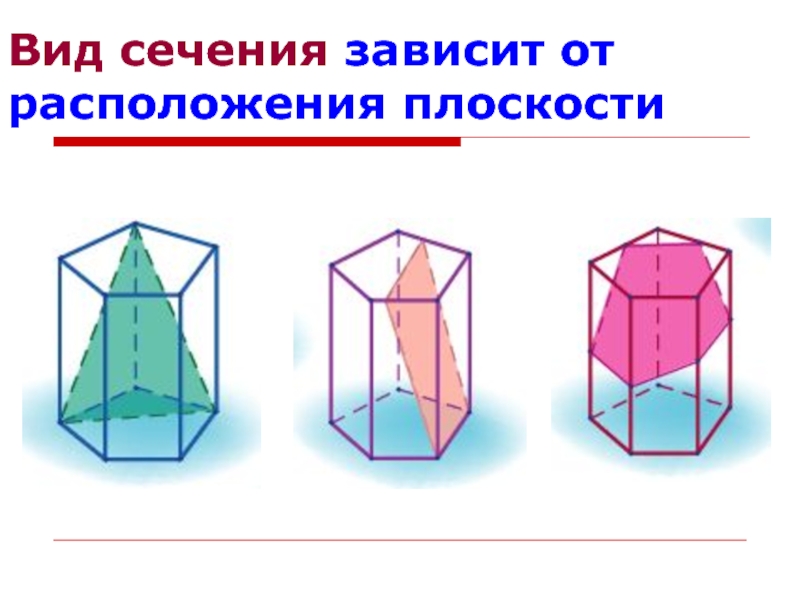
- 6. Вид сечения зависит от расположения плоскости
- 7. Сечения призмы плоскостями, параллельными боковым ребрам,
- 8. Построить сечение призмы плоскостью – означает:
- 9. Методы построения сечений призм
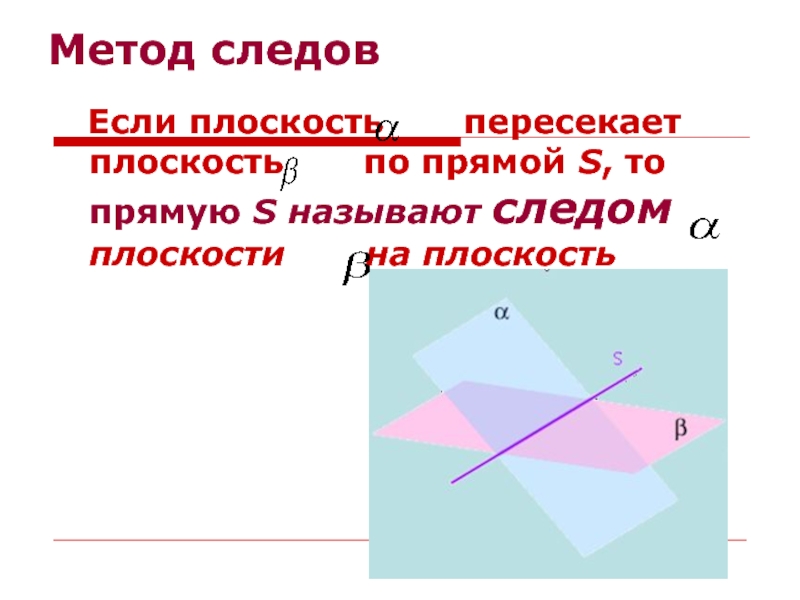
- 10. Метод следов Если плоскость
- 11. Метод следов Метод следов включает
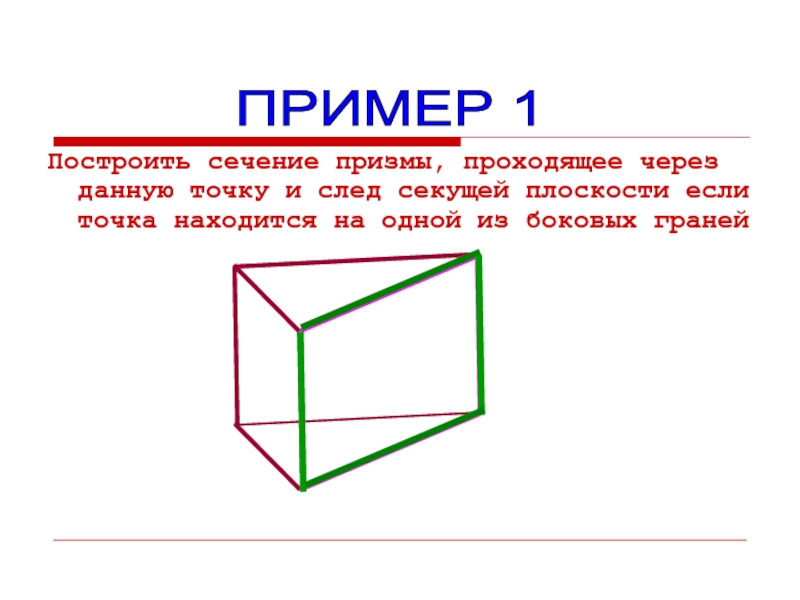
- 12. Построить сечение призмы, проходящее через данную точку
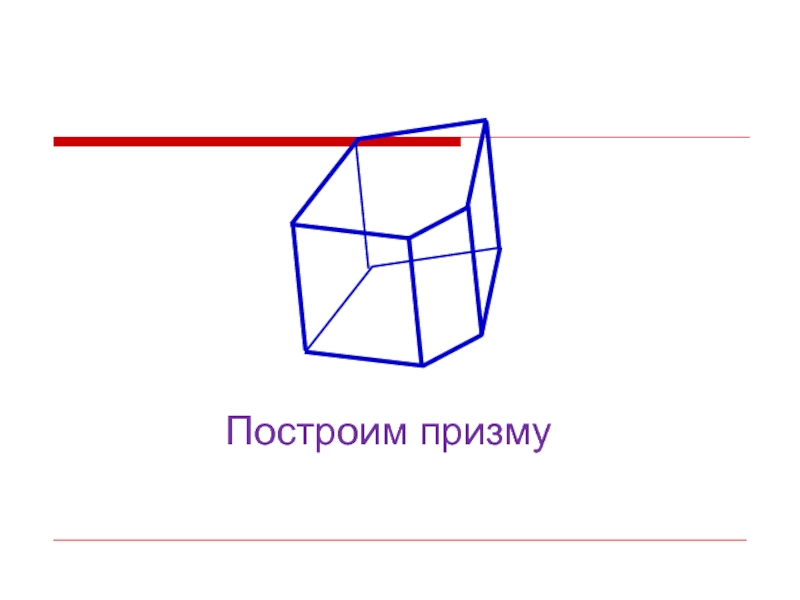
- 13. Построим призму
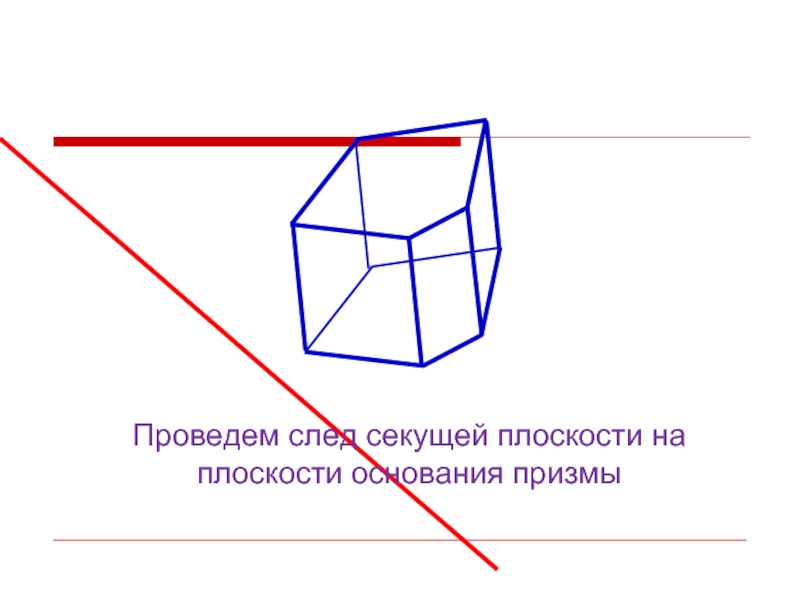
- 14. Проведем след секущей плоскости на плоскости основания призмы
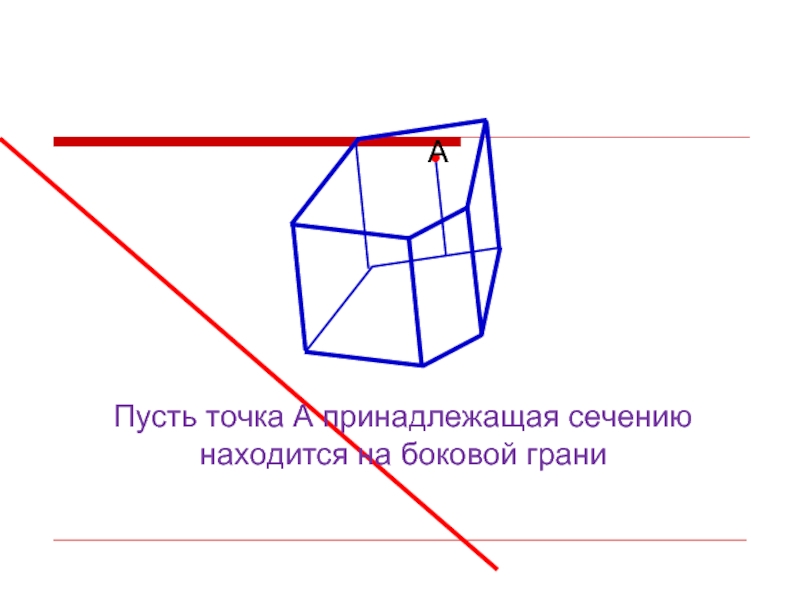
- 15. Пусть точка А принадлежащая сечению находится на боковой грани
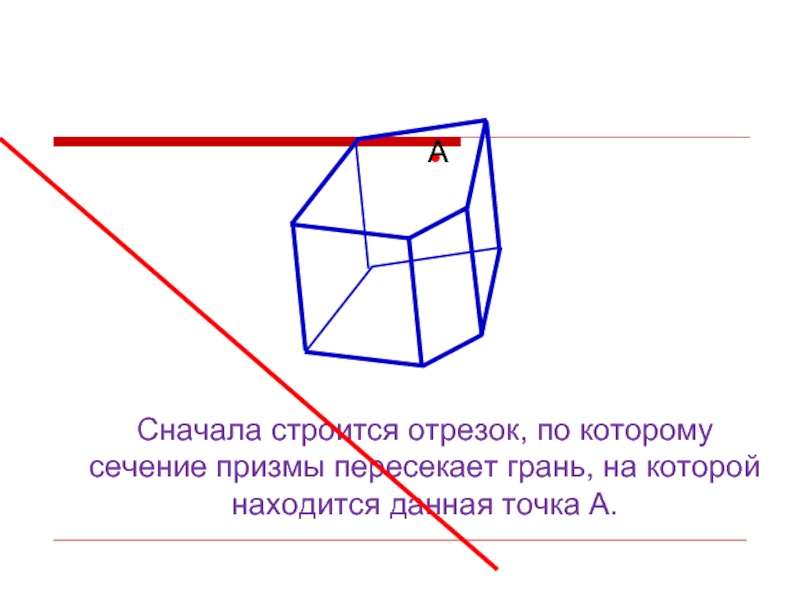
- 16. Сначала строится отрезок, по которому сечение призмы пересекает грань, на которой находится данная точка А.
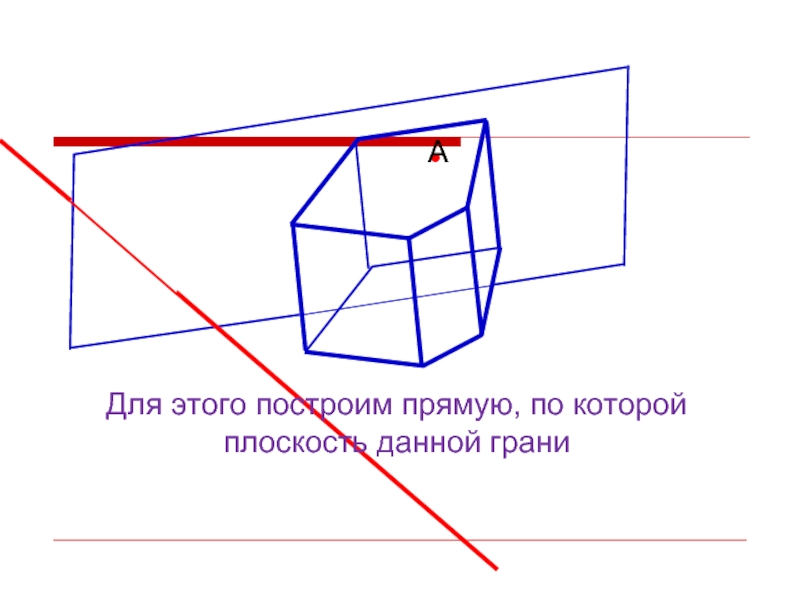
- 17. Для этого построим прямую, по которой плоскость данной грани
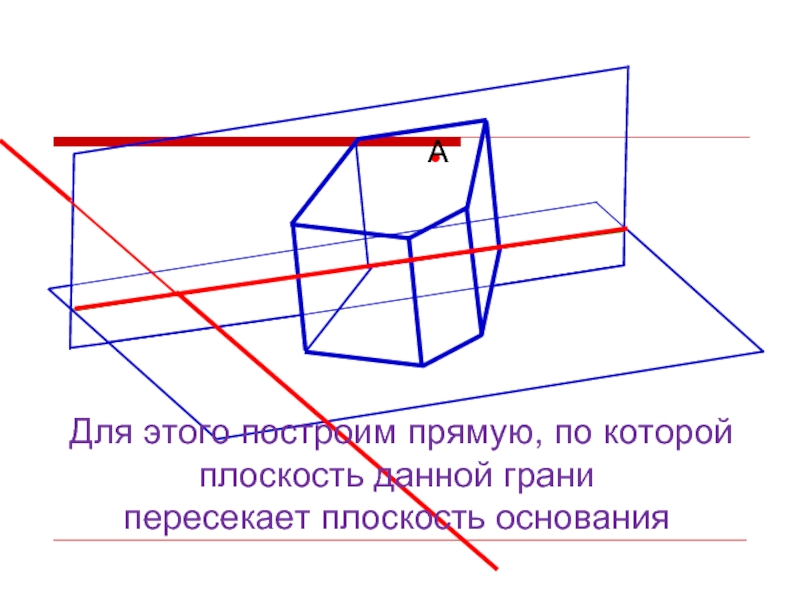
- 18. Для этого построим прямую, по которой
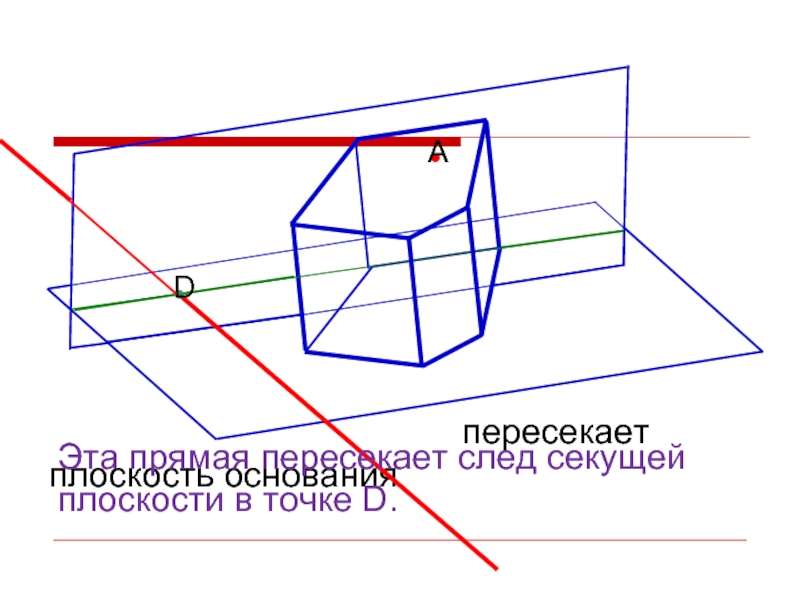
- 20. Эта прямая пересекает след секущей плоскости в
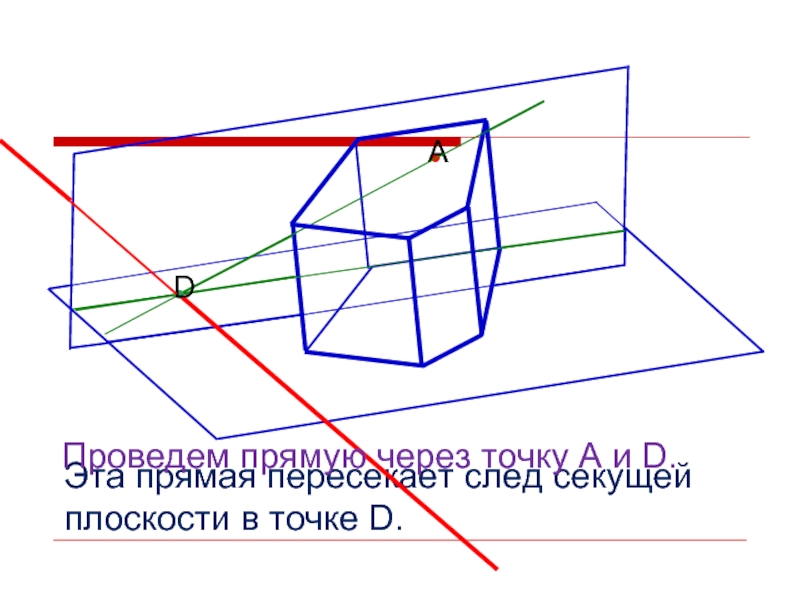
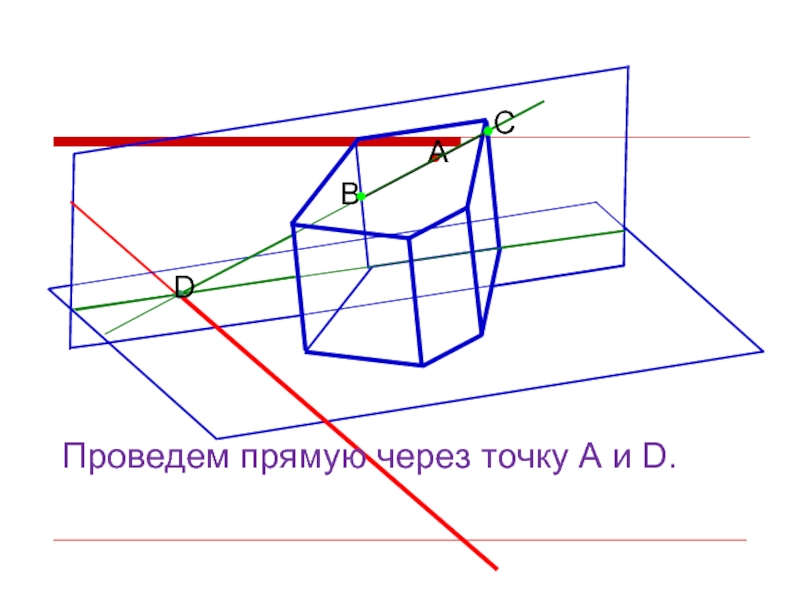
- 21. Проведем прямую через точку А и D.
- 22. В
- 23. Построить сечение призмы, проходящее через данную точку
- 24. Проведем след секущей плоскости призмы Пусть точка
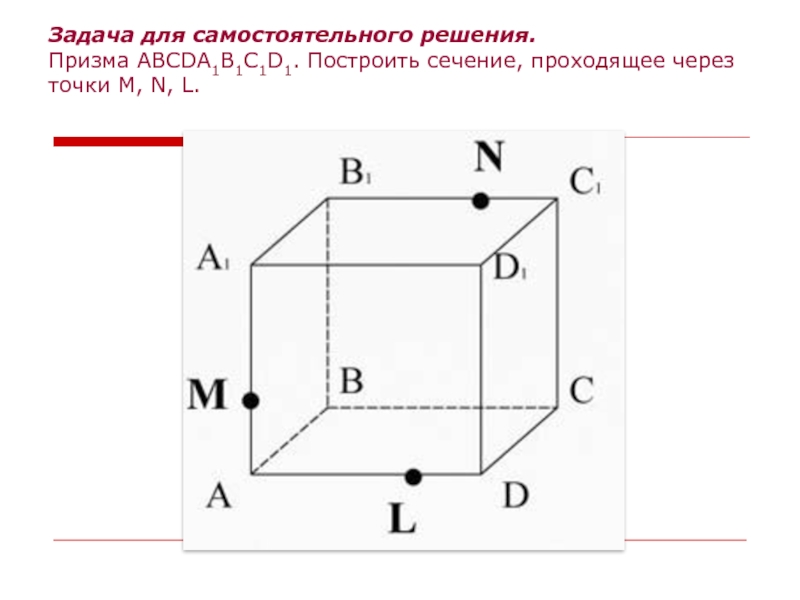
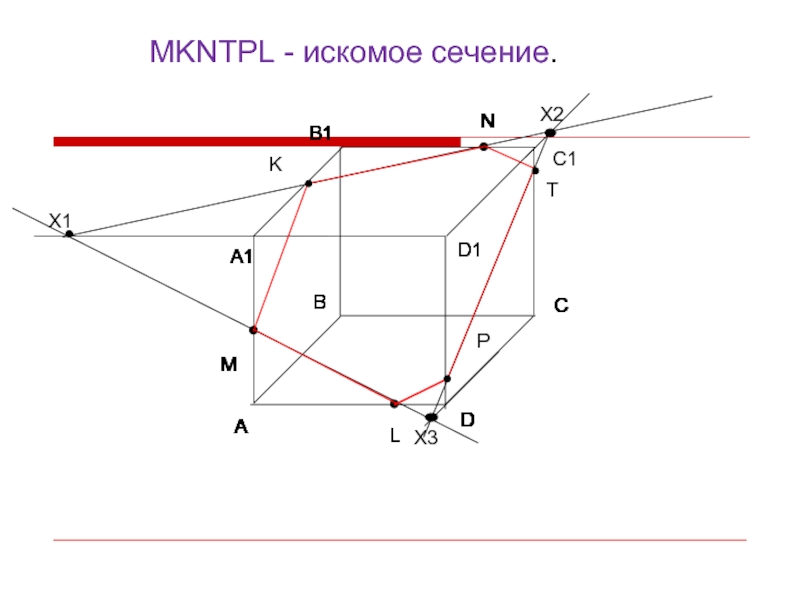
- 25. Задача для самостоятельного решения. Призма ABCDA1B1C1D1.
- 26. A B C D A B C
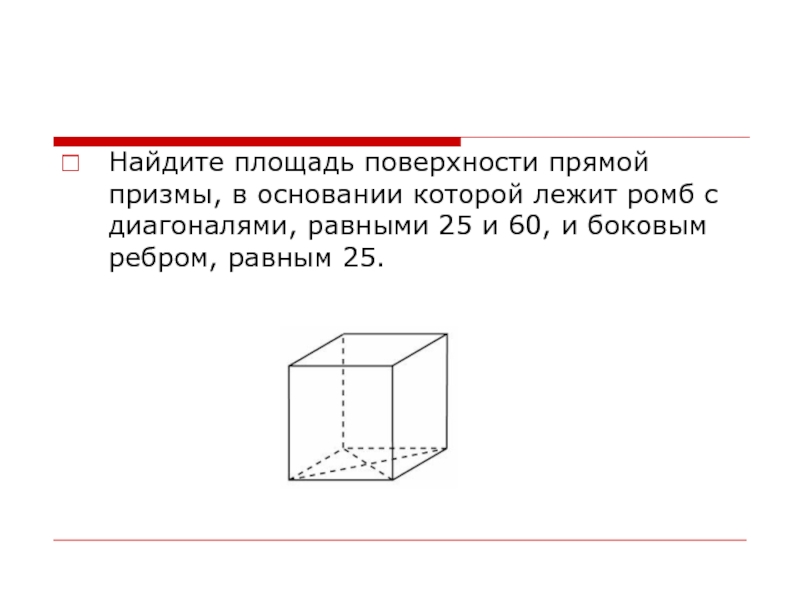
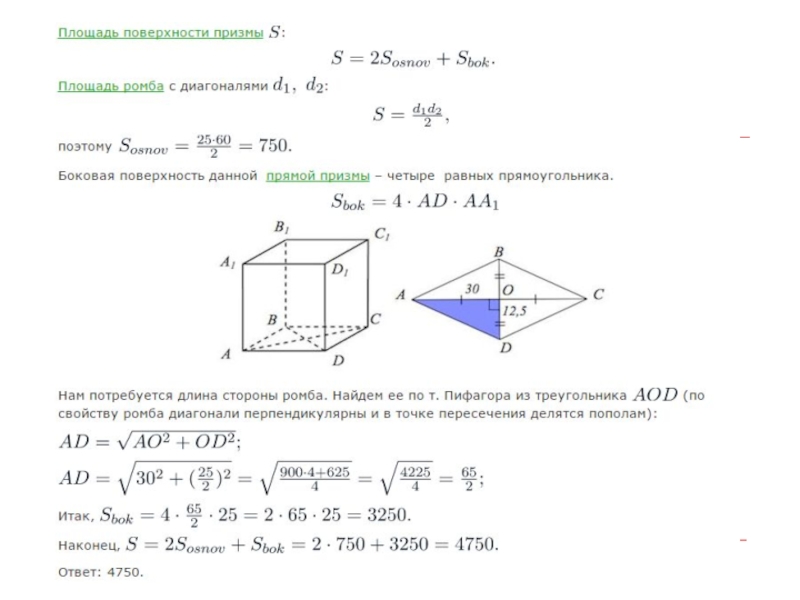
- 27. Найдите площадь поверхности прямой призмы, в основании
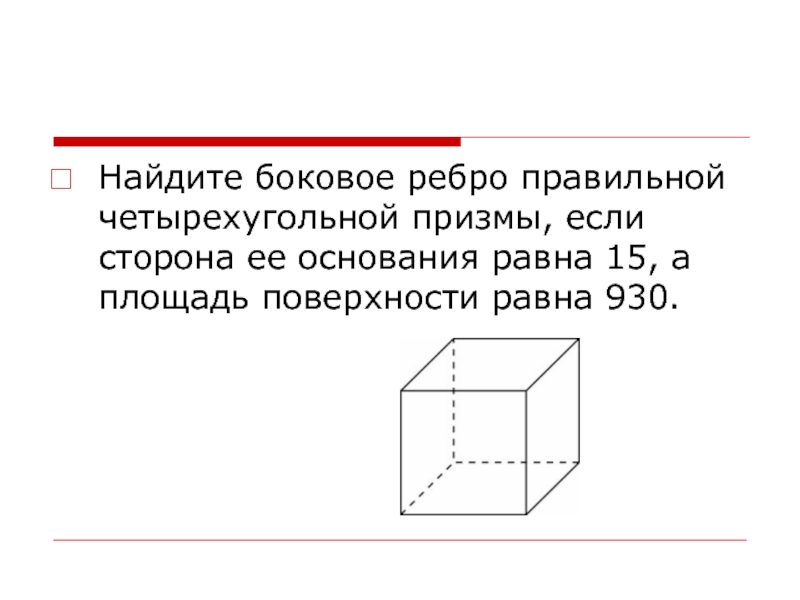
- 29. Найдите боковое ребро правильной четырехугольной призмы, если
- 30. Решение
- 31. Спасибо за внимание!
Для решения многих геометрических задач, необходимо уметь строить сечения призмы различными плоскостями
Слайд 2Для решения многих геометрических задач, необходимо уметь строить сечения призмы различными
плоскостями
Слайд 3Плоская фигура, образовавшаяся при пересечении какой-либо плоскости с пространственной фигурой, называется
плоским сечением
или просто сечением этой фигуры.
Слайд 4
Назовем секущей плоскостью призмы любую плоскость , по обе стороны от
которой имеются точки данной призмы
Многоугольник, сторонами которого являются эти отрезки, называется сечением призмы.
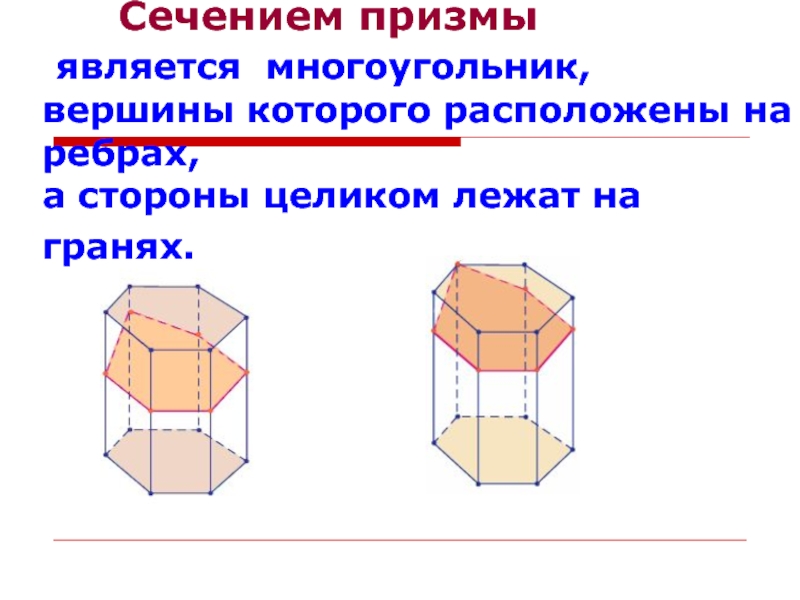
Слайд 5 Сечением призмы является многоугольник, вершины которого расположены
на ребрах,
а стороны целиком лежат на гранях.
Слайд 7
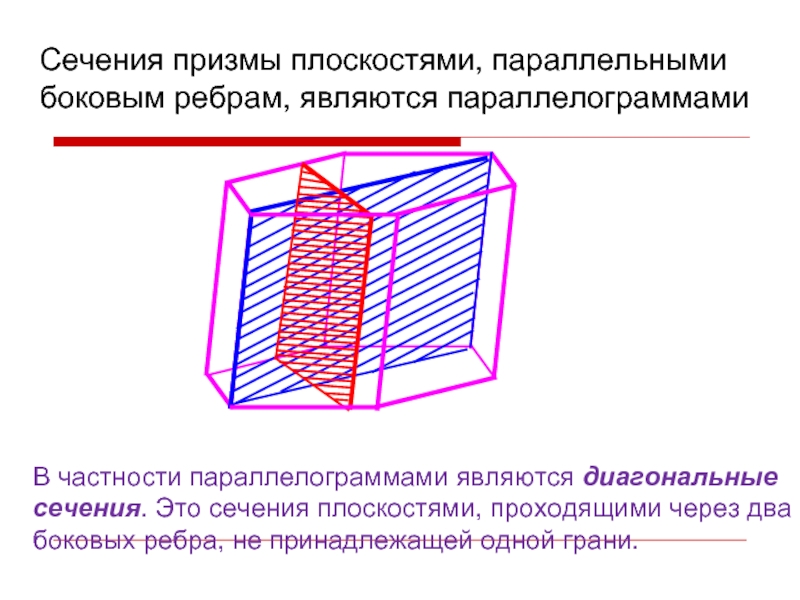
Сечения призмы плоскостями, параллельными боковым ребрам, являются параллелограммами
В частности параллелограммами являются
диагональные сечения. Это сечения плоскостями, проходящими через два боковых ребра, не принадлежащей одной грани.
Слайд 8Построить сечение призмы плоскостью –
означает:
В плоскости каждой пересекаемой
грани
многогранника указать 2-е точки,
принадлежащие сечению;
Соединить их прямой;
Найти точки пересечения прямой с ребрами
призмы.
многогранника указать 2-е точки,
принадлежащие сечению;
Соединить их прямой;
Найти точки пересечения прямой с ребрами
призмы.
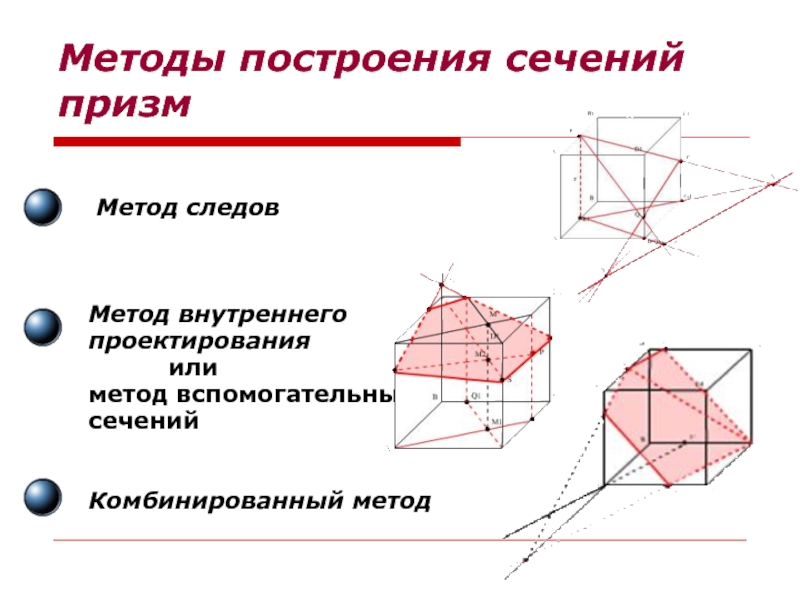
Слайд 9Методы построения сечений призм
Метод следов
Метод
внутреннего
проектирования
или
метод вспомогательных
сечений
Комбинированный метод
проектирования
или
метод вспомогательных
сечений
Комбинированный метод
Слайд 10Метод следов
Если плоскость пересекает плоскость
по прямой S, то прямую S называют следом плоскости на плоскость
Слайд 11Метод следов
Метод следов включает три важных пункта:
Строится линия
пересечения (след) секущей плоскости с плоскостью основания многогранника.
Находим точки пересечения секущей плоскости с ребрами многогранника.
Строим и заштриховываем сечение.
Находим точки пересечения секущей плоскости с ребрами многогранника.
Строим и заштриховываем сечение.
Слайд 12Построить сечение призмы, проходящее через данную точку и след секущей плоскости
если точка находится на одной из боковых граней
ПРИМЕР 1
Слайд 16Сначала строится отрезок, по которому сечение призмы пересекает грань, на которой
находится данная точка А.
Слайд 18 Для этого построим прямую, по которой плоскость данной грани
пересекает плоскость основания
Слайд 22
В
С
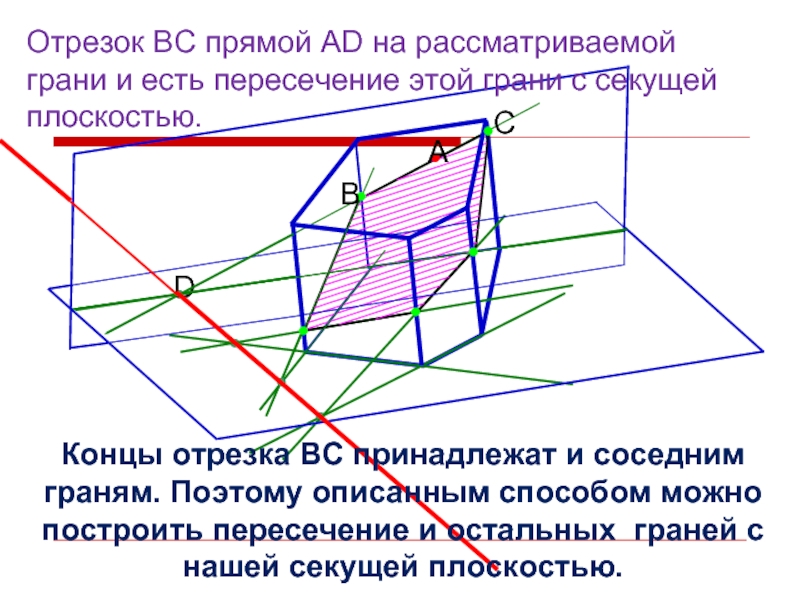
Отрезок ВС прямой АD на рассматриваемой грани и есть пересечение этой
грани с секущей плоскостью.
Концы отрезка ВС принадлежат и соседним граням. Поэтому описанным способом можно построить пересечение и остальных граней с нашей секущей плоскостью.
Слайд 23Построить сечение призмы, проходящее через данную точку и след секущей плоскости
если данная точка находится на верхнем основании
ПРИМЕР 2
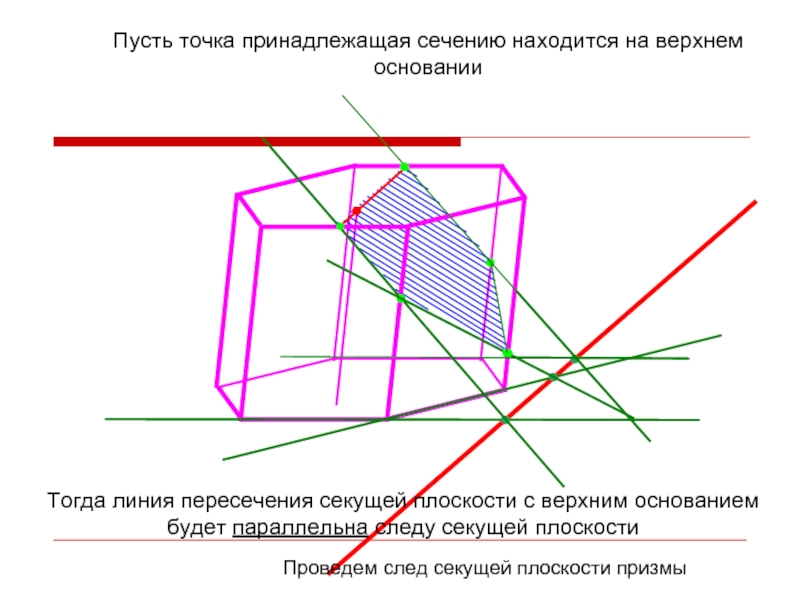
Слайд 24Проведем след секущей плоскости призмы
Пусть точка принадлежащая сечению находится на верхнем
основании
Тогда линия пересечения секущей плоскости с верхним основанием будет параллельна следу секущей плоскости
Слайд 25 Задача для самостоятельного решения. Призма ABCDA1B1C1D1. Построить сечение, проходящее через точки M,
N, L.
Слайд 26A
B
C
D
A
B
C
A
B
D
A
B
D
A
C
B
D
A
C1
B1
D1
A1
M
L
N
A
D
A
C
D
A
C
D
A
N
C
D
A
B1
N
C
D
A
A1
B1
N
D
A
M
A1
B1
N
C
D
A
L
M
A1
B1
N
C
D
A
D1
L
M
A1
B1
N
C
D
A
B
D1
L
M
A1
B1
N
A
X1
K
T
P
MKNTPL - искомое сечение.
Слайд 27Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с
диагоналями, равными 25 и 60, и боковым ребром, равным 25.
Слайд 29Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна
15, а площадь поверхности равна 930.
