- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Классическая линейная регрессия презентация
Содержание
- 1. Классическая линейная регрессия
- 2. Понятие о парной и множественной линейной регрессии
- 3. Регрессия это функциональная зависимость между объясняющими переменными
- 4. Множественная линейная регрессия Парная линейная
- 5. Причины возникновения εi не включение в уравнение
- 6. Очередность «появления» параметров и переменных в регрессионном
- 7. Ограниченность парной линейной регрессии: никакая единственная независимая
- 8. Сущность метода наименьших квадратов и способы нахождения параметров уравнения
- 9. Сущность метода наименьших квадратов
- 11. Свойства оценок параметров регрессионного уравнения: Несмещенность оценок
- 12. / n
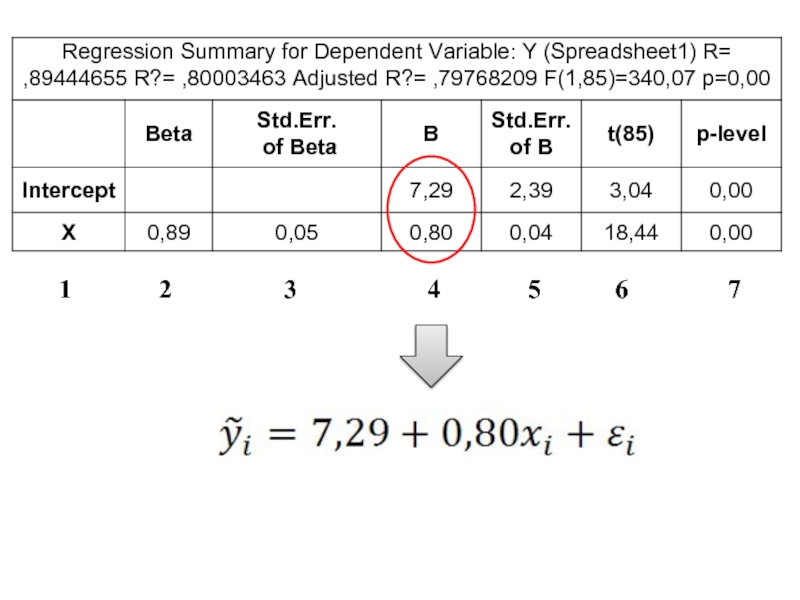
- 14. 1 2 3 4 5 6 7
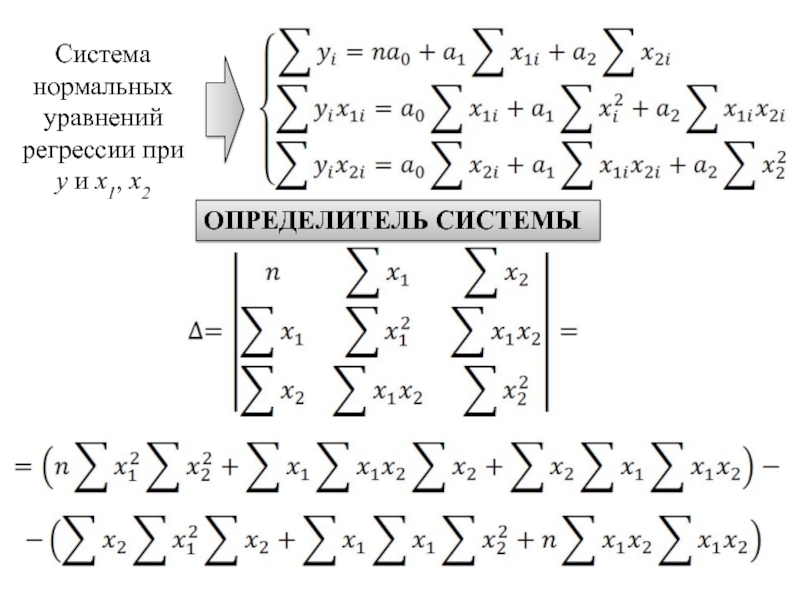
- 16. ОПРЕДЕЛИТЕЛЬ СИСТЕМЫ
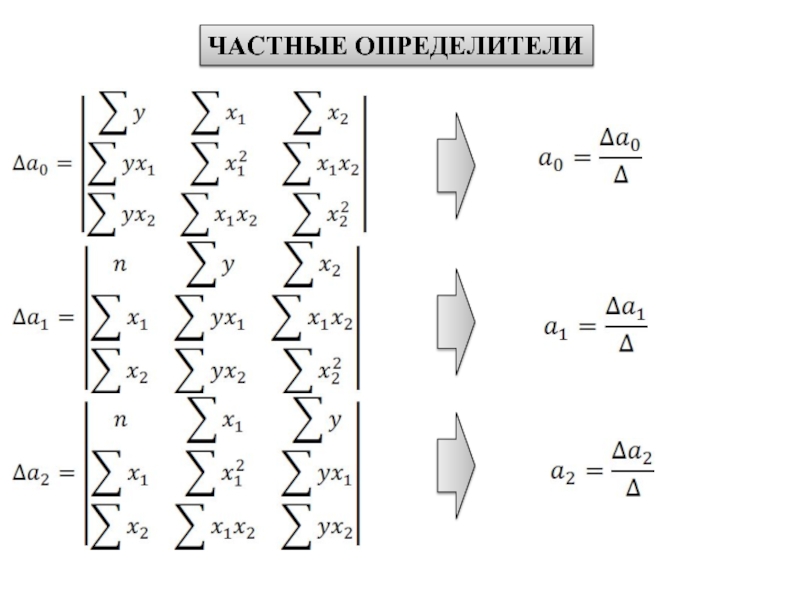
- 17. ЧАСТНЫЕ ОПРЕДЕЛИТЕЛИ
- 18. Y=XА+Е А = (XTX)-1XTY
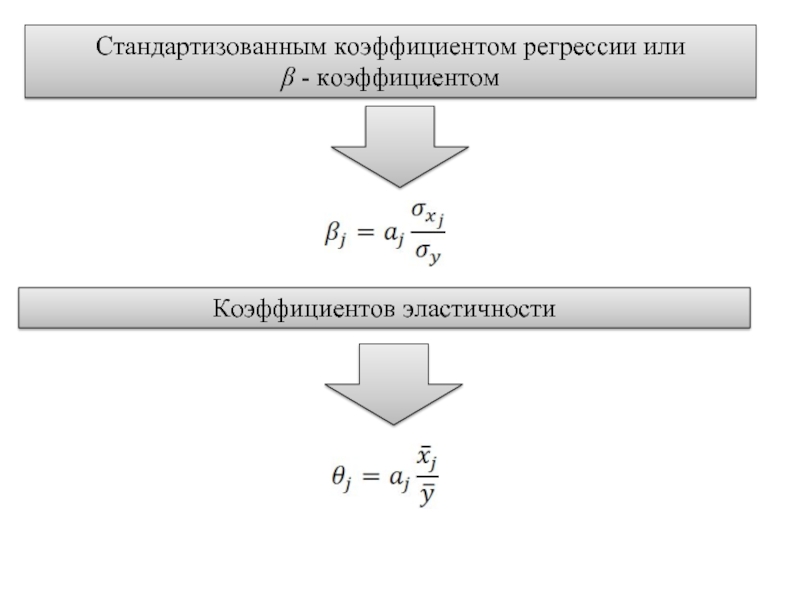
- 20. Стандартизованным коэффициентом регрессии или β -
- 21. Регрессионное уравнение в стандартизированной форме
Слайд 1Классическая линейная регрессия
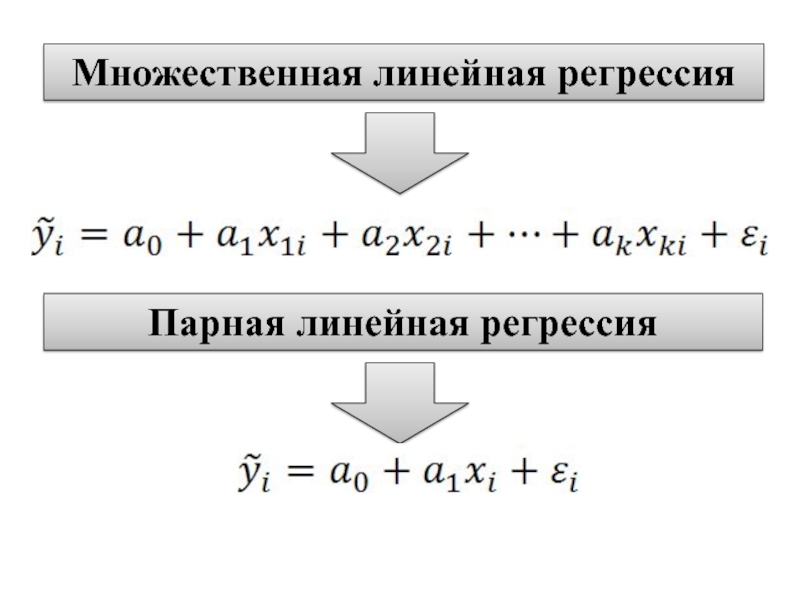
Понятие о парной и множественной линейной регрессии
Сущность метода наименьших
квадратов и способы нахождения параметров уравнения
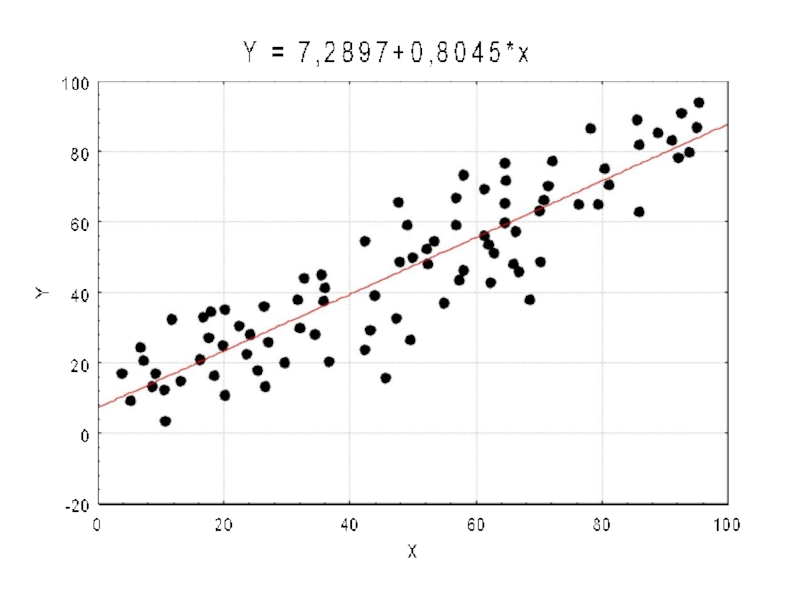
Слайд 3Регрессия это функциональная зависимость между объясняющими переменными и условным математическим ожиданием
(средним значением) зависимой переменой, которая строится с целью предсказания (прогноз) этого среднего значения при фиксированных значениях первых (регрессоров).
Слайд 5Причины возникновения εi
не включение в уравнение факторов оказывающих существенное влияние на
результативный показатель;
трудности и ошибки при измерении данных;
неверный выбор функциональной формы модели;
агрегирование переменных;
непредсказуемость человеческого фактора;
ограниченность статистических данных.
трудности и ошибки при измерении данных;
неверный выбор функциональной формы модели;
агрегирование переменных;
непредсказуемость человеческого фактора;
ограниченность статистических данных.
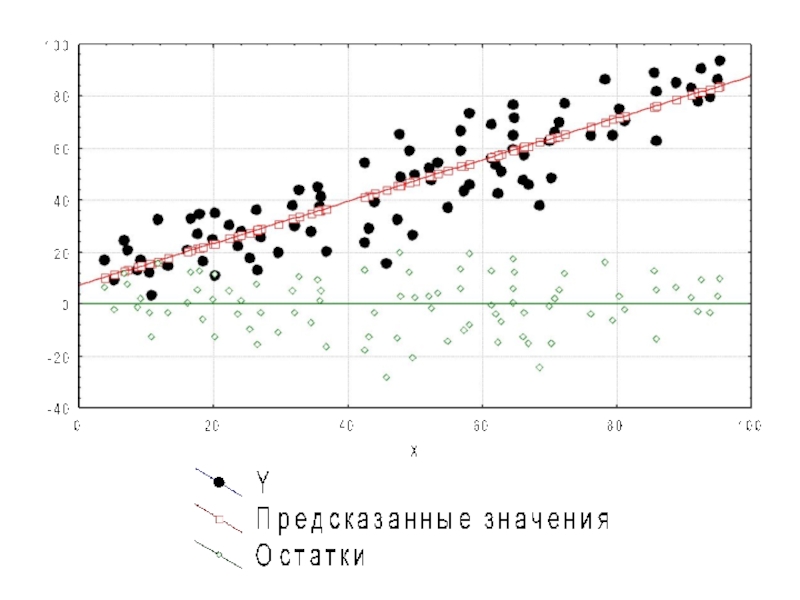
Слайд 6Очередность «появления» параметров и переменных в регрессионном уравнении:
имеем n штук пар
наблюдений
находим параметры уравнения
находим теоретические значения зависимой переменной
находим значения случайного члена
находим параметры уравнения
находим теоретические значения зависимой переменной
находим значения случайного члена
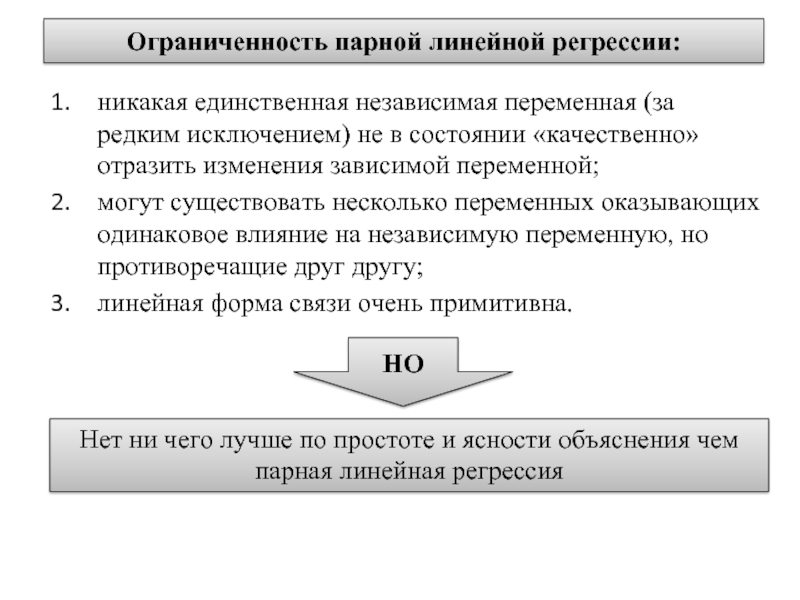
Слайд 7Ограниченность парной линейной регрессии:
никакая единственная независимая переменная (за редким исключением) не
в состоянии «качественно» отразить изменения зависимой переменной;
могут существовать несколько переменных оказывающих одинаковое влияние на независимую переменную, но противоречащие друг другу;
линейная форма связи очень примитивна.
могут существовать несколько переменных оказывающих одинаковое влияние на независимую переменную, но противоречащие друг другу;
линейная форма связи очень примитивна.
НО
Нет ни чего лучше по простоте и ясности объяснения чем парная линейная регрессия
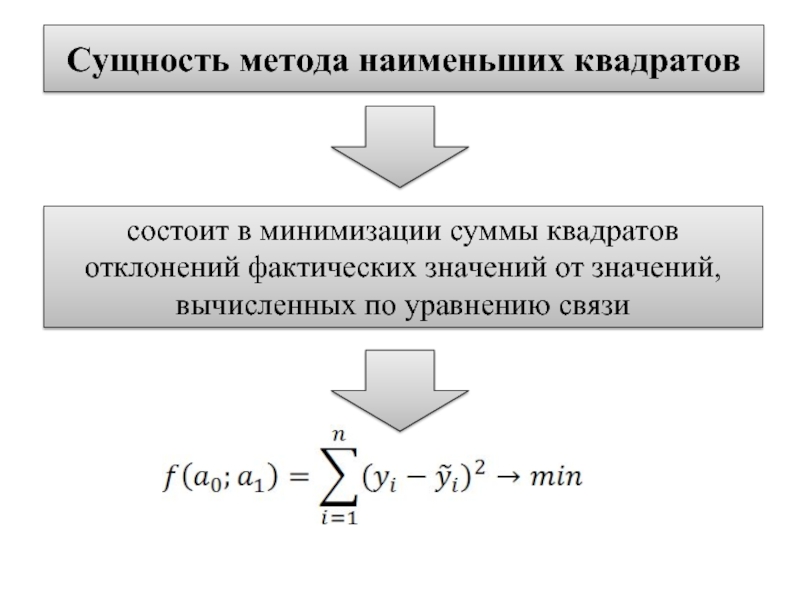
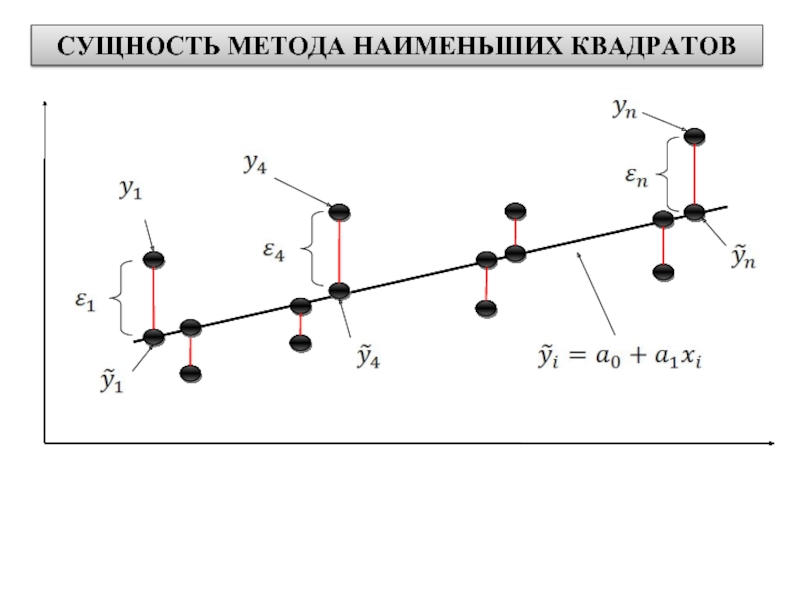
Слайд 9Сущность метода наименьших квадратов
состоит в минимизации суммы квадратов отклонений фактических значений
от значений, вычисленных по уравнению связи
Слайд 11Свойства оценок параметров регрессионного уравнения:
Несмещенность оценок параметров регрессии
Состоятельность оценок параметров регрессии
Эффективность
оценок параметров регрессии
Достаточность оценки
Достаточность оценки
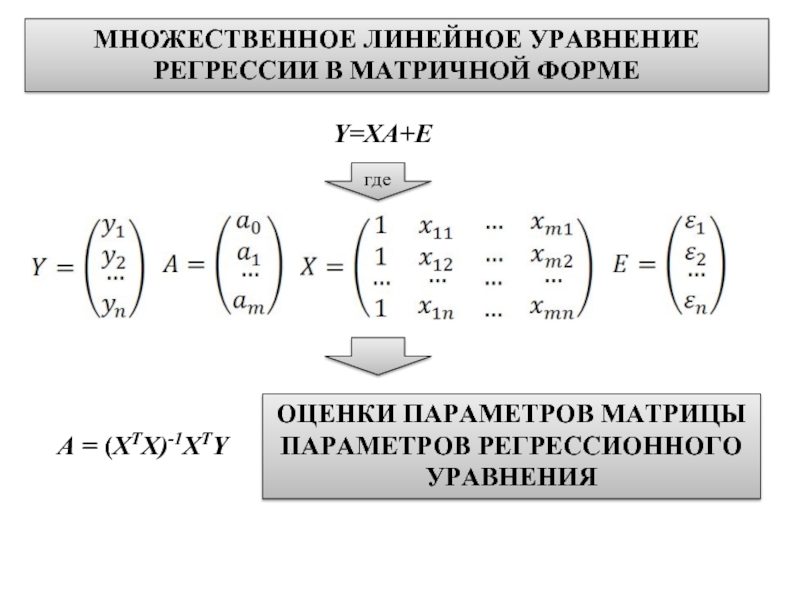
Слайд 18Y=XА+Е
А = (XTX)-1XTY
МНОЖЕСТВЕННОЕ ЛИНЕЙНОЕ УРАВНЕНИЕ РЕГРЕССИИ В МАТРИЧНОЙ ФОРМЕ
ОЦЕНКИ ПАРАМЕТРОВ
МАТРИЦЫ ПАРАМЕТРОВ РЕГРЕССИОННОГО УРАВНЕНИЯ
где