№ 110»
Руководитель: Байгильдина Разиля Валитовна,
учитель математики
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Исследовательская работа на тему Изопериметрические задачи презентация
Содержание
- 1. Исследовательская работа на тему Изопериметрические задачи
- 2. Объект исследования: изопериметрическая задача. Предмет исследования: приемы
- 3. Актуальность Выбранную нами тему считаю актуальной, потому
- 4. Одна из таких задач – задача Дидоны,
- 5. Слово «изопериметрический» происходит от слов «изос» (по-гречески
- 6. S S
- 7. Легенда о Дидоне
- 8. Метод Якоба Штейнера Решение изопериметрической задачи
- 9. Решение:
- 11. Теоремы Всякая максимальная фигура выпукла. Всякая
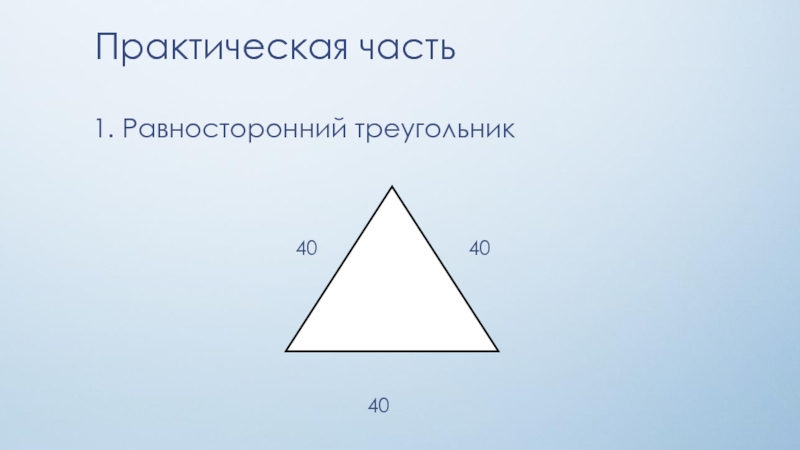
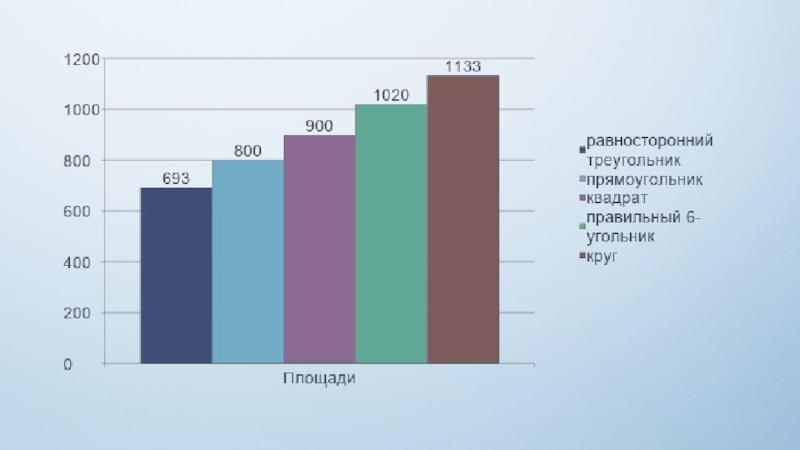
- 12. Практическая часть 40 40 40 1. Равносторонний треугольник
- 13. 2. Прямоугольник 40 20
- 14. 3. Квадрат 30 30
- 15. 4. Шестиугольник 20 20
- 16. 5. Круг L = 120
- 18. Решение задач
- 19. 2. Почему канализационный люк круглый?
- 20. 3. Задача Пахома Крестьянин Пахом, который мечтал
- 22. Итоги Для достижения цели нами были проведены
- 23. Спасибо за внимание!
Слайд 1
Исследовательская работа
на тему
«Изопериметрические задачи»
Выполнила: Гарипова Рания,
ученица 7А класса МБОУ «Школа
Слайд 2Объект исследования: изопериметрическая задача.
Предмет исследования: приемы решений изопериметрической задачи.
Цель исследования: выявить
и обосновать математические средства для решения изопериметрических задач
Задачи:
понять, что входит в термин изопериметрической задачи;
рассмотреть доказательства некоторых изопериметрических задач;
научиться решать изопериметрические задачи
Гипотеза: среди геометрических фигур с равными периметрами наибольшую площадь имеет круг.
Задачи:
понять, что входит в термин изопериметрической задачи;
рассмотреть доказательства некоторых изопериметрических задач;
научиться решать изопериметрические задачи
Гипотеза: среди геометрических фигур с равными периметрами наибольшую площадь имеет круг.
Слайд 3Актуальность
Выбранную нами тему считаю актуальной, потому что такие задачи не только
очень важны в математике и ее приложениях, но и красивы.
Изопериметрические задачи часто возникают в инженерных расчетах, архитектуре, экономике, а так же находят свое применение в науках о природе: физике, химии, биологии.
Изопериметрические задачи часто возникают в инженерных расчетах, архитектуре, экономике, а так же находят свое применение в науках о природе: физике, химии, биологии.
Слайд 4Одна из таких задач – задача Дидоны, которая имеет несколько различных
формулировок.
О них я и хочу рассказать.
О них я и хочу рассказать.
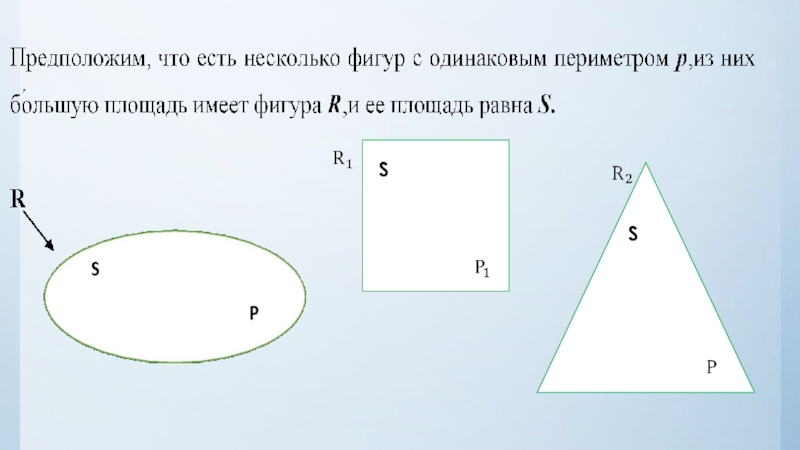
Слайд 5Слово «изопериметрический» происходит от слов «изос» (по-гречески «равный») и «периметр». Изопериметрическая
задача (на плоскости) состоит в нахождении фигуры, имеющей наибольшую площадь среди всех фигур с одним и тем же периметром.
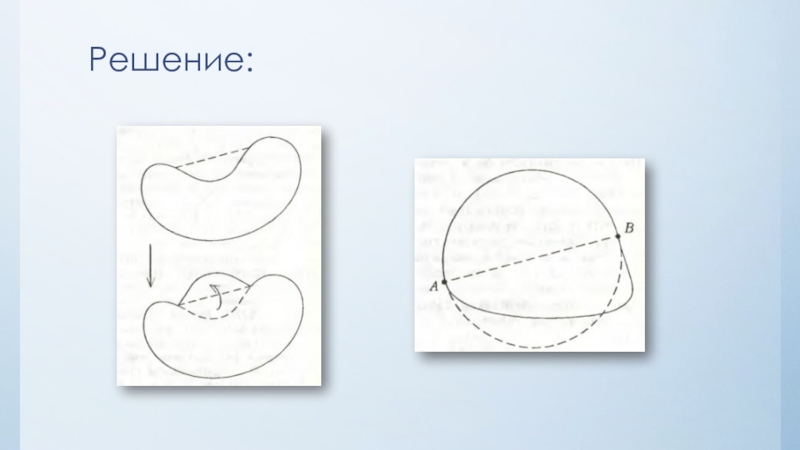
Слайд 8Метод Якоба Штейнера
Решение изопериметрической задачи было найдено выдающимся швейцарским геометром
XIX столетия Якобом Штейнером (1796-1863).
Задача звучит следующим образом: Среди всевозможных плоских замкнутых линий заданной длины найдите ту, которая ограничивает фигуру наибольшей площади.
Задача звучит следующим образом: Среди всевозможных плоских замкнутых линий заданной длины найдите ту, которая ограничивает фигуру наибольшей площади.
Слайд 11Теоремы
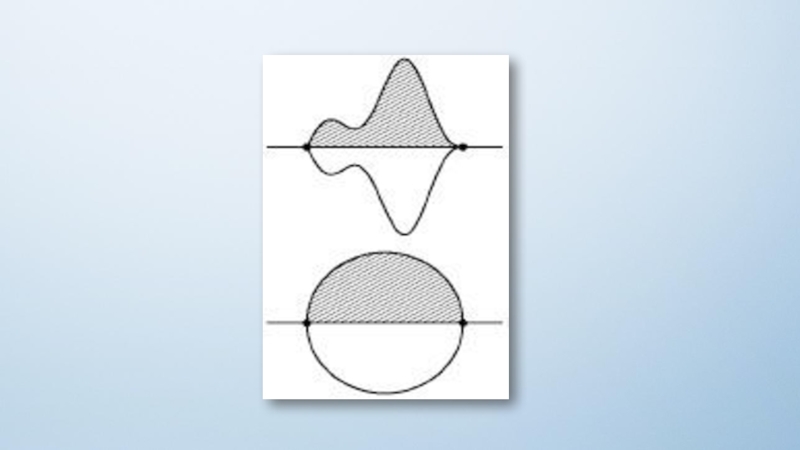
Всякая максимальная фигура выпукла.
Всякая хорда максимальной фигуры с периметром р, делящая
пополам ее периметр, обязательно делит ровно пополам и ее площадь.
Слайд 203. Задача Пахома
Крестьянин Пахом, который мечтал о собственной земле и собрал,
наконец, желанную сумму, предстал перед требованием старшины:
«Сколько за день земли обойдешь, вся твоя будет за 1000р. Но если к заходу солнца не возвратишься на место, с которого вышел, пропали твои деньги».
Выбежал утром Пахом, прибежал на место и упал без чувств, обежав четырехугольник периметром Р=40 км.
P=AB+BC+CD+AD=40
S=(2+10)/2*13=78
«Сколько за день земли обойдешь, вся твоя будет за 1000р. Но если к заходу солнца не возвратишься на место, с которого вышел, пропали твои деньги».
Выбежал утром Пахом, прибежал на место и упал без чувств, обежав четырехугольник периметром Р=40 км.
P=AB+BC+CD+AD=40
S=(2+10)/2*13=78
Слайд 22Итоги
Для достижения цели нами были проведены эксперименты, решены задачи и обоснована
изопериметрическая проблема: среди геометрических фигур на плоскости с равными периметрами наибольшую площадь имеет круг.
Изопериметрические задачи - это не только пример старинной математики, но и задачи, которые встречаются каждому из нас в реальной жизни.
Изопериметрические задачи - это не только пример старинной математики, но и задачи, которые встречаются каждому из нас в реальной жизни.