руководитель: к. ф.-м. н.
Карташов А.В.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Использование триангуляции при моделировании сложных объектов презентация
Содержание
- 1. Использование триангуляции при моделировании сложных объектов
- 2. Постановка задачи: Прямоугольная область (a,b) с набором
- 3. Задача: 1. Построить триангуляцию. 2. Моделировать поведение точек, используя триангуляцию и перестраивая ее при необходимости.
- 4. «Жадный» алгоритм построения триангуляции Шаг 1.
- 5. Поведение точек при столкновении: а) Столкновение
- 6. Поведение точек при столкновении: б) Столкновение с
- 7. Проведение расчетов: Рассчитаем время пересечения точкой
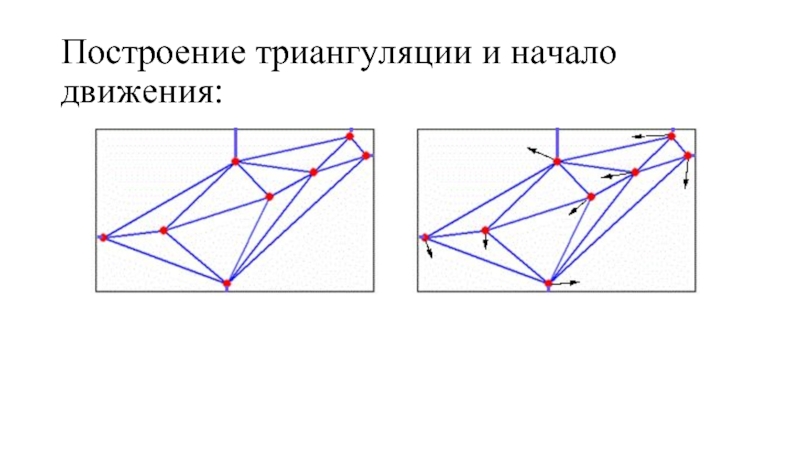
- 8. Построение триангуляции и начало движения:
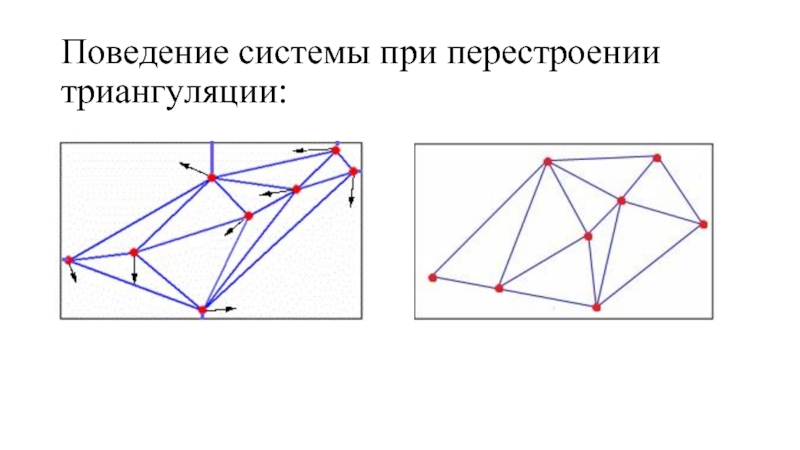
- 9. Поведение системы при перестроении триангуляции:
Слайд 1Использование триангуляции при моделировании сложных объектов
Автор: студент 325 группы
Ловкайтес В. С.
Научный
Слайд 2Постановка задачи:
Прямоугольная область (a,b) с набором точек внутри:
Задана область.
n – количество
точек.
Начальные
координаты
Начальная
скорость
Начальные
координаты
Начальная
скорость
Слайд 3Задача:
1. Построить триангуляцию.
2. Моделировать поведение точек, используя триангуляцию и перестраивая ее
при необходимости.
Слайд 4«Жадный» алгоритм построения триангуляции
Шаг 1. Генерируется список всех возможных отрезков,
соединяющих пары исходных точек, и он сортируется по длинам отрезков.
Шаг 2. Начиная с самого короткого, последовательно выполняется вставка отрезков в триангуляцию. Если отрезок не пересекается с другими ранее вставленными отрезками, то он вставляется, иначе он отбрасывается.
Скорость работы алгоритма составляет 0(n log n+n) для отрезков и ~0(n) для точек.
Скорость работы алгоритма составляет 0(n log n+n) для отрезков и ~0(n) для точек.
Слайд 5Поведение точек при столкновении:
а) Столкновение двух точек или точки с областью
При столкновении двух точек или точки с областью, они отталкиваются, согласно закону сохранения импульса для абсолютно упругих тел:
Слайд 6Поведение точек при столкновении:
б) Столкновение с границей треугольника
При столкновении точки
с областью, один из треугольников пропадает, то есть его площадь равна 0. Рассчитаем площадь по формуле:
, где
, где
Слайд 7Проведение расчетов:
Рассчитаем время пересечения точкой границы треугольника:
Xi=xi+vixt
Yi=yi+viyt
После подставки в расчетную
формулу получим квадратное уравнение At2+Bt+C=0 с коэффициентами:
А: v1yv2x+v2yv1x-v2yv3x+v3yv2x-v3yv3x-v3yv1x+v3xv1y
B: y1v2x-x2v1y+y2v1x-y2v2x+x1v2y+y2v2x-y2v3x-x3v2y+y3v2x+x2v3y-y3v1x-x1v3y+y1v3x+x3v1y
C: -x2y1+y2x1-y2x3+y3x2-y3x1+y1x3
А: v1yv2x+v2yv1x-v2yv3x+v3yv2x-v3yv3x-v3yv1x+v3xv1y
B: y1v2x-x2v1y+y2v1x-y2v2x+x1v2y+y2v2x-y2v3x-x3v2y+y3v2x+x2v3y-y3v1x-x1v3y+y1v3x+x3v1y
C: -x2y1+y2x1-y2x3+y3x2-y3x1+y1x3