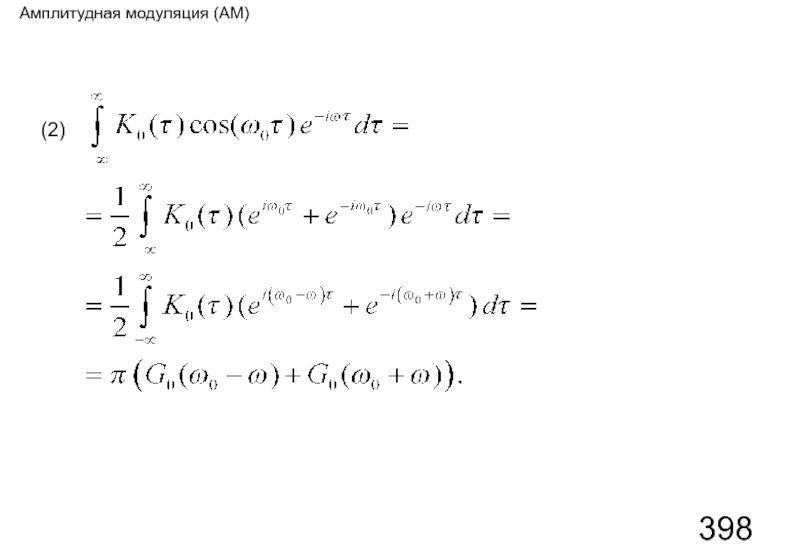- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Статистическая радиофизика. Модели случайных процессов. (Тема 4) презентация
Содержание
- 1. Статистическая радиофизика. Модели случайных процессов. (Тема 4)
- 2. Общий план курса Случайные процессы и методы
- 3. Модели случайных процессов (план) см [1]. Глава
- 4. Спектральный анализ сигналов Периодические сигналы
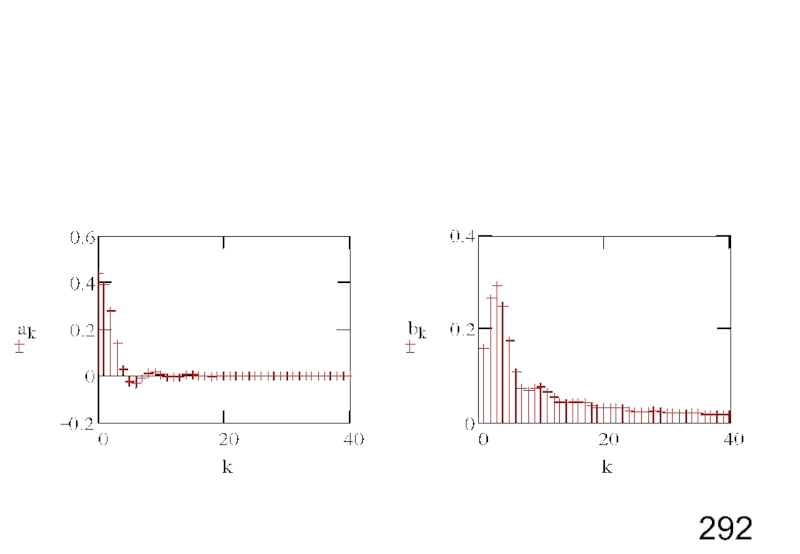
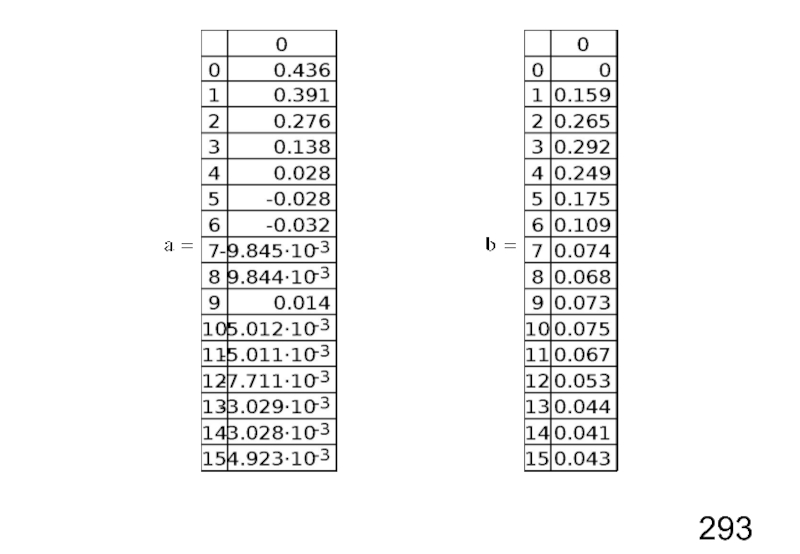
- 5. Коэффициенты разложения ряда Фурье
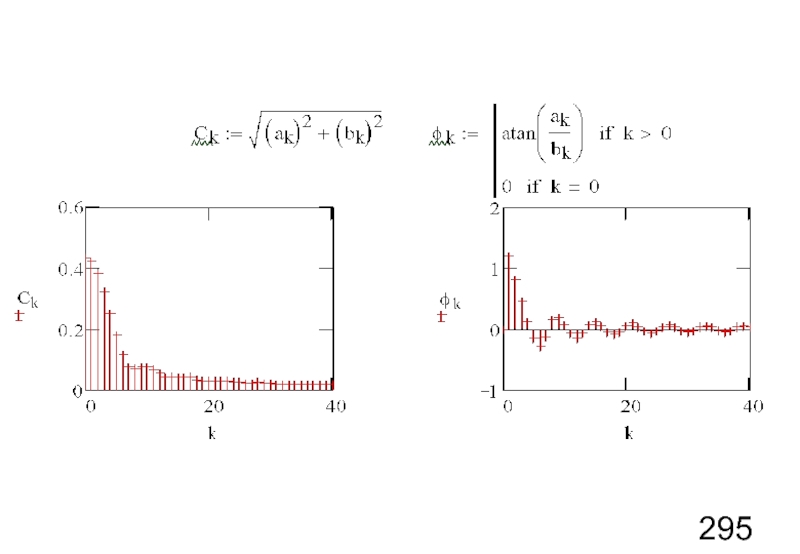
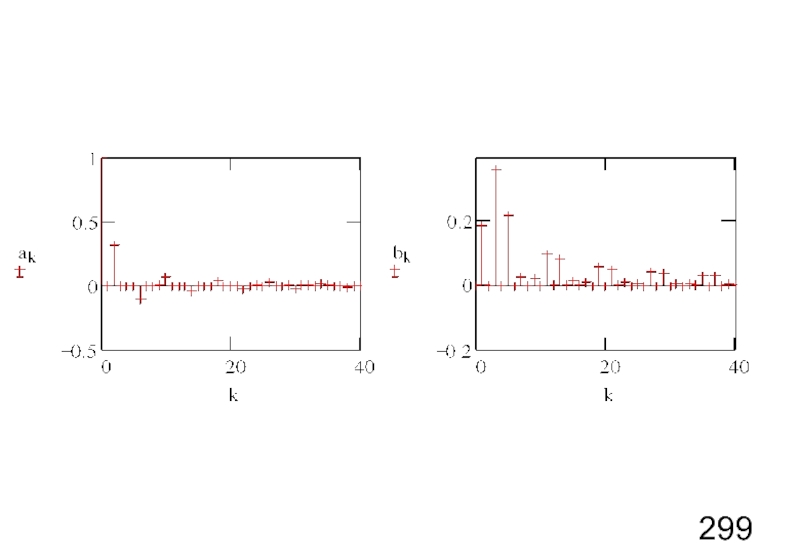
- 6. Формы представления ряда Фурье
- 7. Формы представления ряда Фурье
- 8. Пример 1. Периодическая последовательность косинусоидальных импульсов.
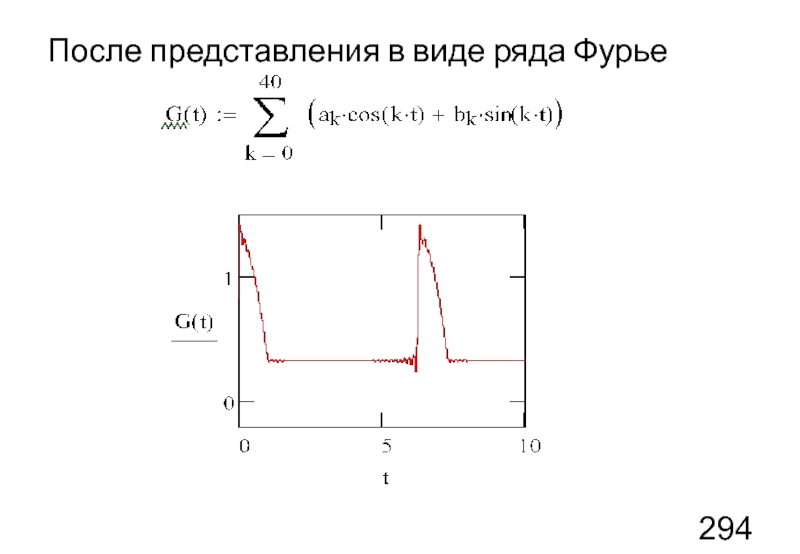
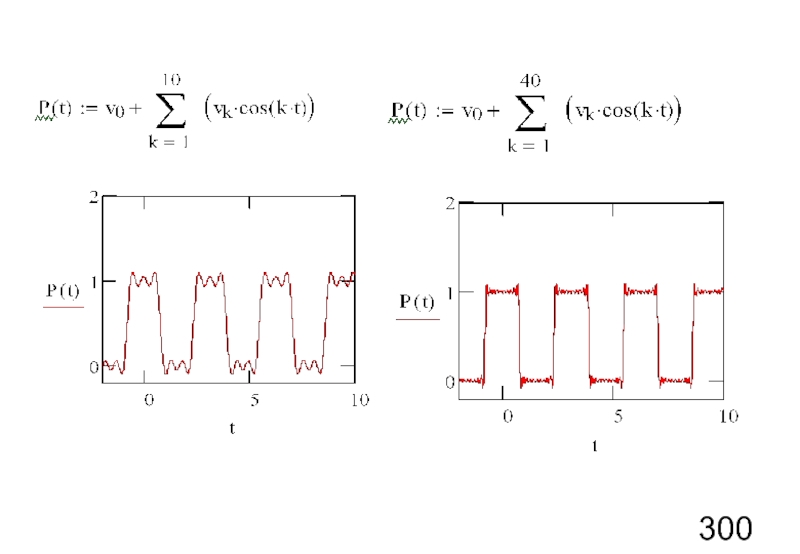
- 13. После представления в виде ряда Фурье
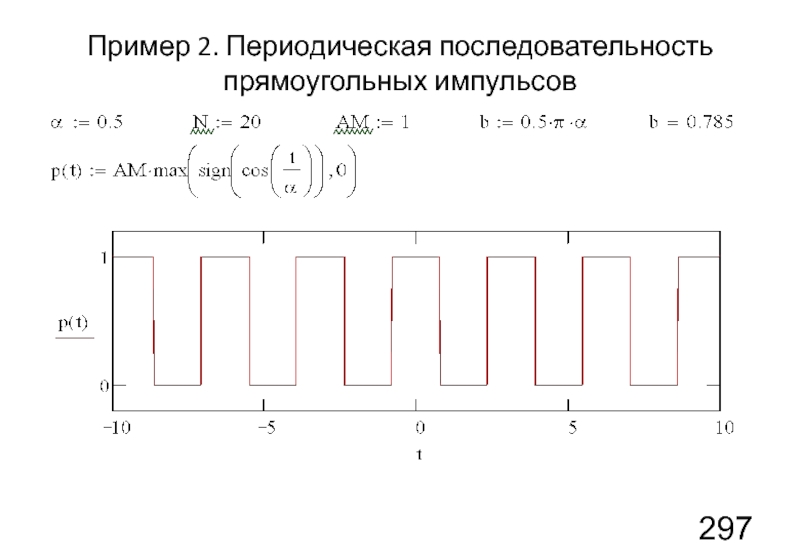
- 16. Пример 2. Периодическая последовательность прямоугольных импульсов
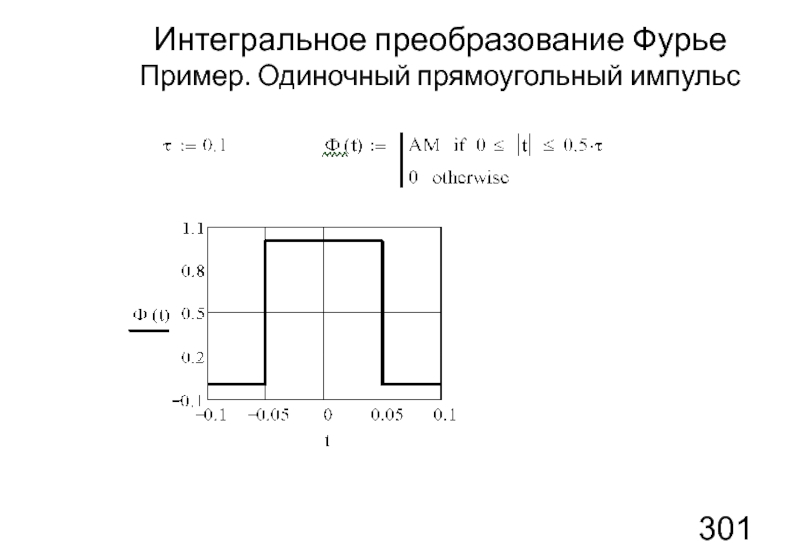
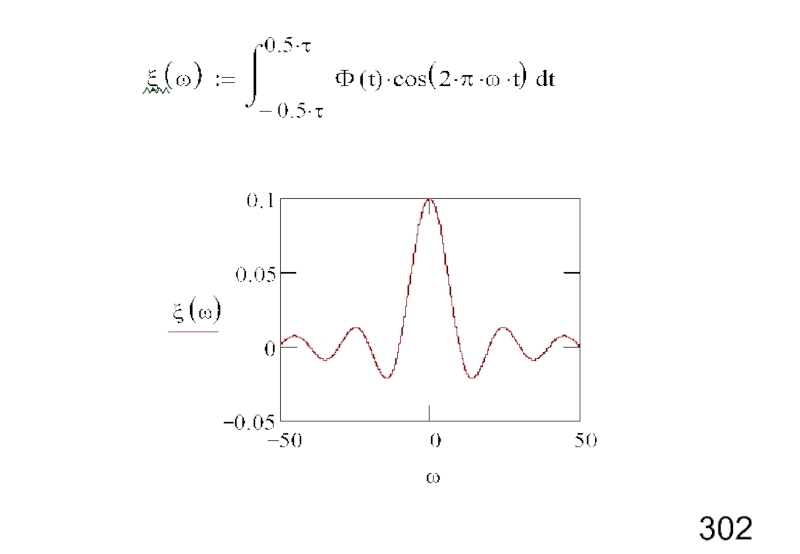
- 20. Интегральное преобразование Фурье Пример. Одиночный прямоугольный импульс
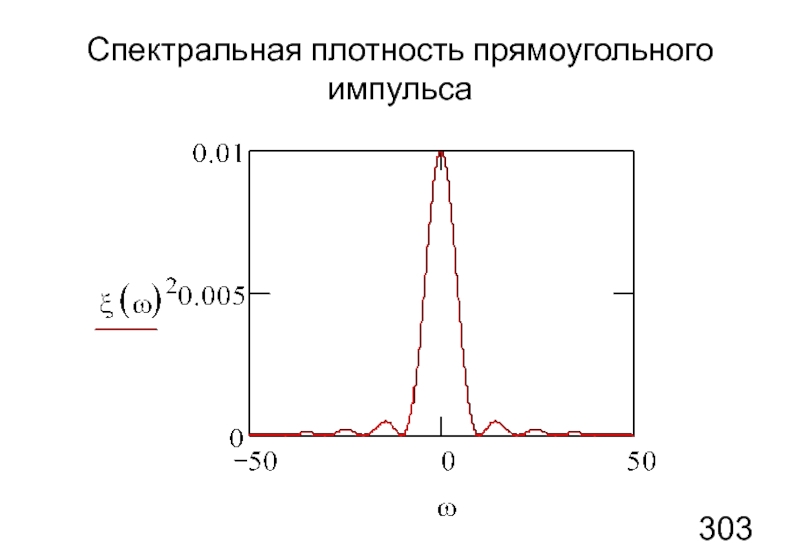
- 22. Спектральная плотность прямоугольного импульса
- 23. Модели случайных процессов (план) см [1]. Глава
- 24. Гауссовский случайный процесс Многомерная гауссовская плотность вероятности Смысл параметров гауссовской плотности вероятности:
- 25. Гауссовский случайный процесс-2 Одномерная плотность вероятности
- 26. Гауссовский случайный процесс-3 Одномерная плотность вероятности примет
- 27. Гауссовский случайный процесс-4 Свойства одномерного распределения. Отличны от нуля лишь четные центральные моменты
- 28. Гауссовский случайный процесс-5 Реализация в Mathcad.
- 29. Гауссовский случайный процесс-6 Применение для случайных процессов
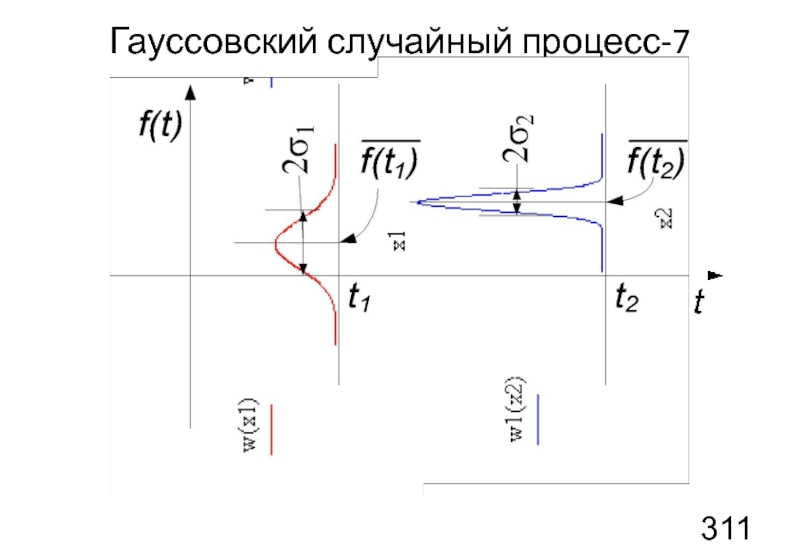
- 30. Гауссовский случайный процесс-7
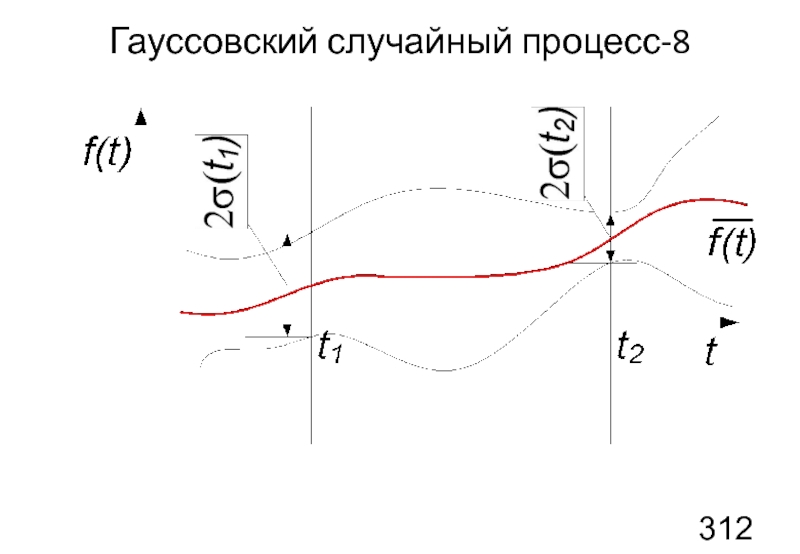
- 31. Гауссовский случайный процесс-8
- 32. Гауссовский случайный процесс-9 Для вычисления корреляционного момента
- 33. Гауссовский процесс-10
- 34. Гауссовский процесс-11 Таким образом, плотность вероятности может
- 35. Гауссовский процесс-12
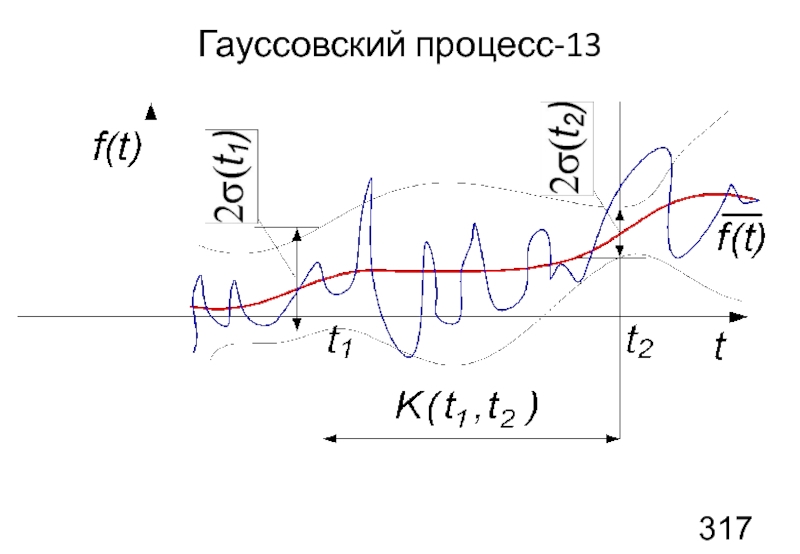
- 36. Гауссовский процесс-13
- 37. Гауссовский случайный процесс-14 Выводы: 1. Если процесс
- 38. Модели случайных процессов (план) см [1]. Глава
- 39. Узкополосный стационарный шум Шум узкополосный, если спектральная
- 40. Узкополосный стационарный шум -2 Δω
- 41. Узкополосный стационарный шум -2 Флуктуационную компоненту представим
- 42. Вместо огибающей и фазы также вводят квадратурные
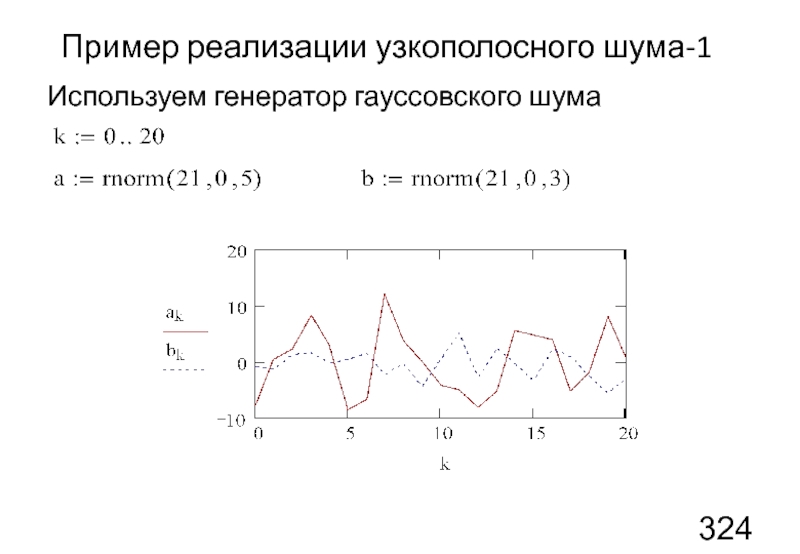
- 43. Пример реализации узкополосного шума-1 Используем генератор гауссовского шума
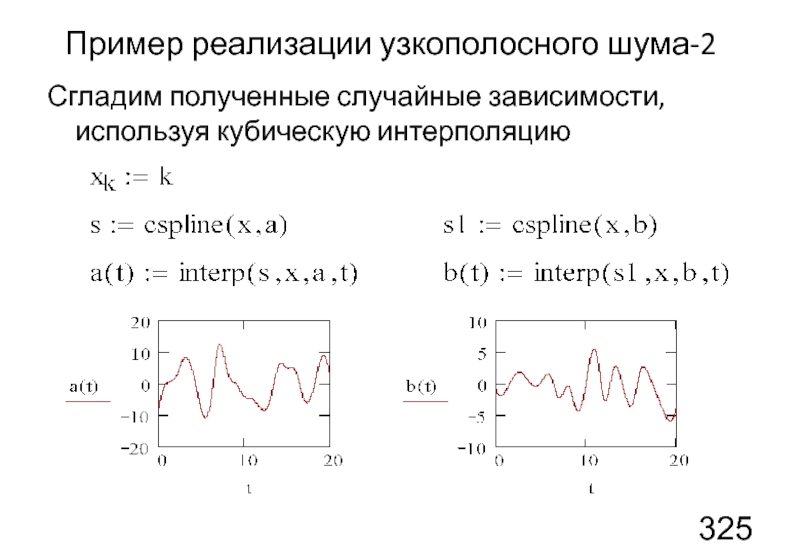
- 44. Пример реализации узкополосного шума-2 Сгладим полученные случайные зависимости, используя кубическую интерполяцию
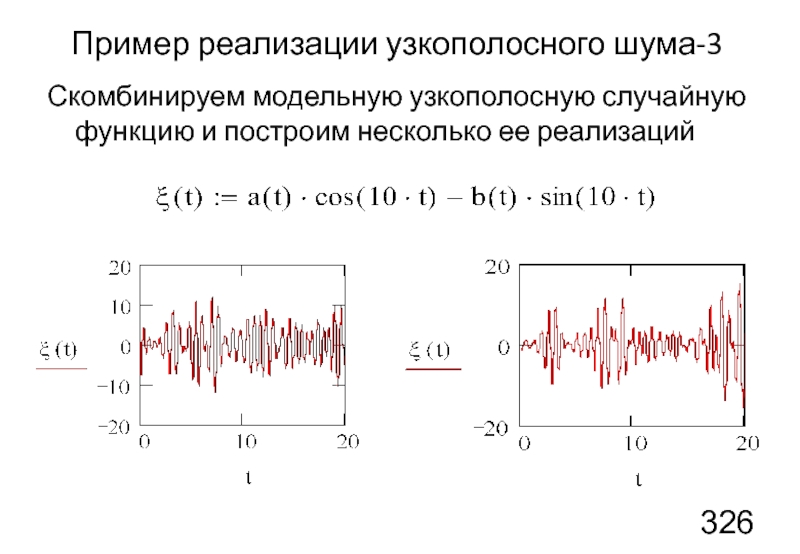
- 45. Пример реализации узкополосного шума-3 Скомбинируем модельную узкополосную случайную функцию и построим несколько ее реализаций
- 46. Постановка задачи: Задача: зная свойства шума ξ(t)
- 47. Корреляционные и спектральные характеристики квадратурных компонент Предполагаем,
- 48. Считаем известной корреляционную функцию Подставим в
- 49. Учтем известные тригонометрические формулы Подставим эти выражения в приведенное выше выражение
- 50. В силу стационарности здесь не должно быть
- 51. Где введена безразмерная корреляционная функция
- 52. Чтобы найти неизвестные функции воспользуемся формулой
- 55. При этом предположении Имеет свойства корреляционной функции
- 56. Модели случайных процессов (план) см [1]. Глава
- 57. Узкополосный стационарный гауссовский шум
- 58. Найдем плотность вероятности переменных и
- 59. Проинтегрируем по углам и получим распределение по Полученное распределение носит название распределения Релея (Рэлея)
- 60. Моменты распределения Рэлея:
- 61. Используем полученные результаты для анализа суперпозиции гармонического
- 62. Будем искать вероятностные характеристики огибающей и
- 63. Будем искать распределение по ρ
- 65. Более подробно о модифицированной функции Бесселя см.
- 67. Замечание об использовании Mathcad. В Mathcad
- 68. Обсуждение результатов В пределе сильного шума, когда μ
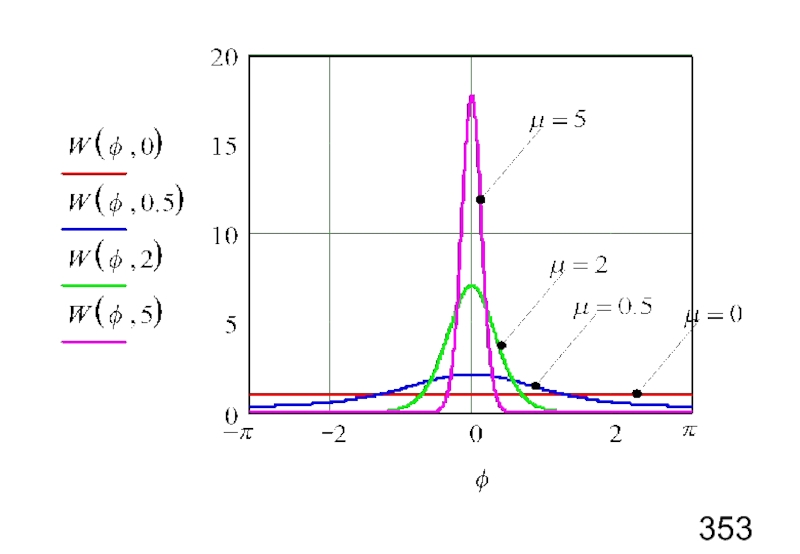
- 69. Распределение фазы
- 70. В предельных случаях
- 71. Построение графика W(φ,μ) средствами Mathcad где использована
- 73. Модели случайных процессов (план) см [1].
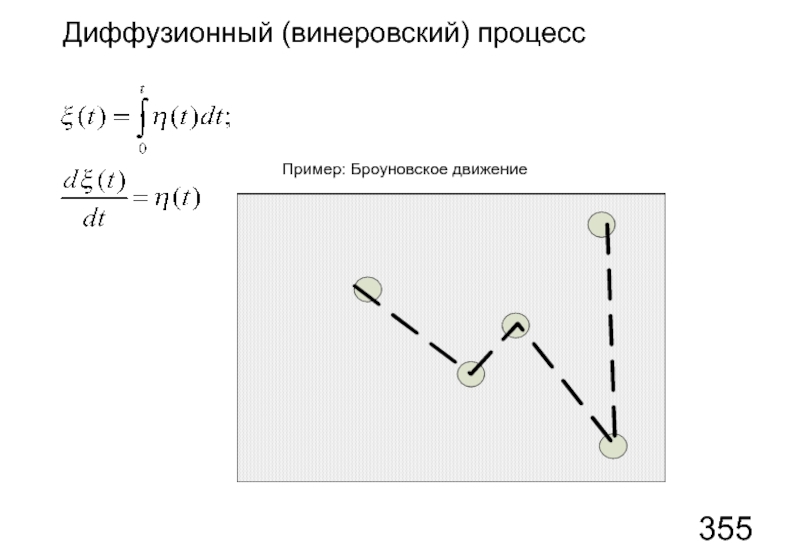
- 74. Диффузионный (винеровский) процесс Пример: Броуновское движение
- 75. переопределение времени
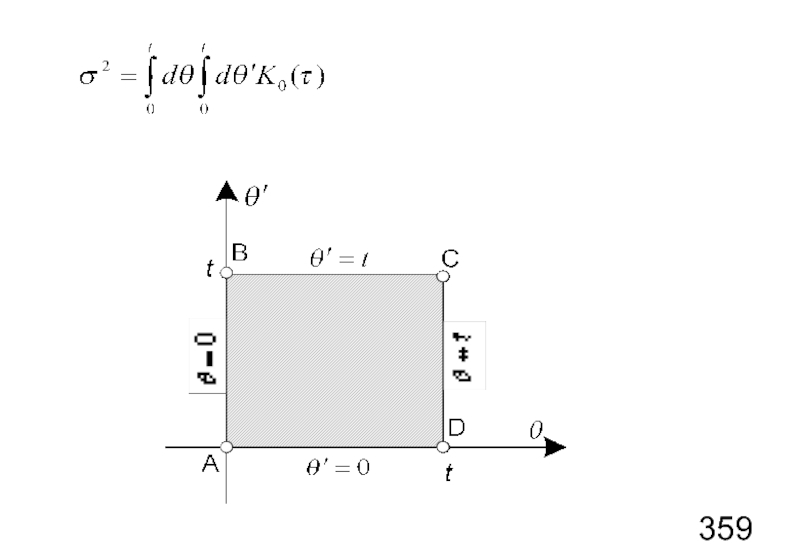
- 76. Постановка задачи: найти вероятностные свойства процесса
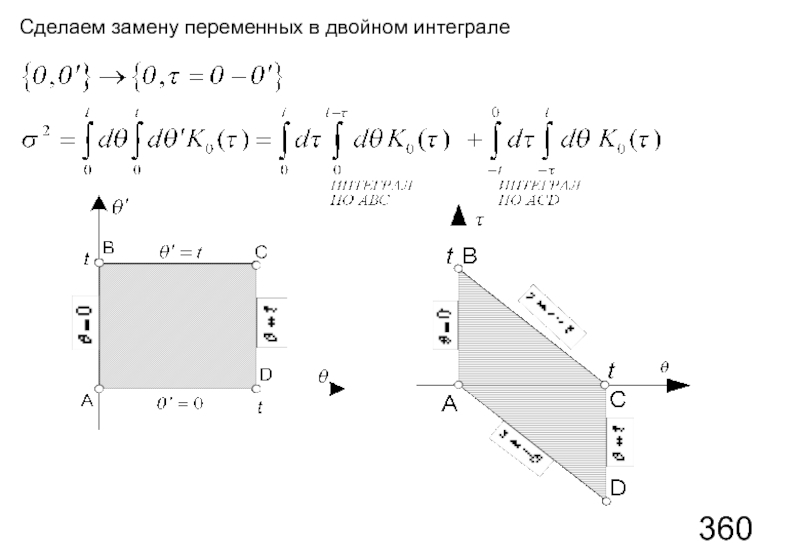
- 79. Сделаем замену переменных в двойном интеграле
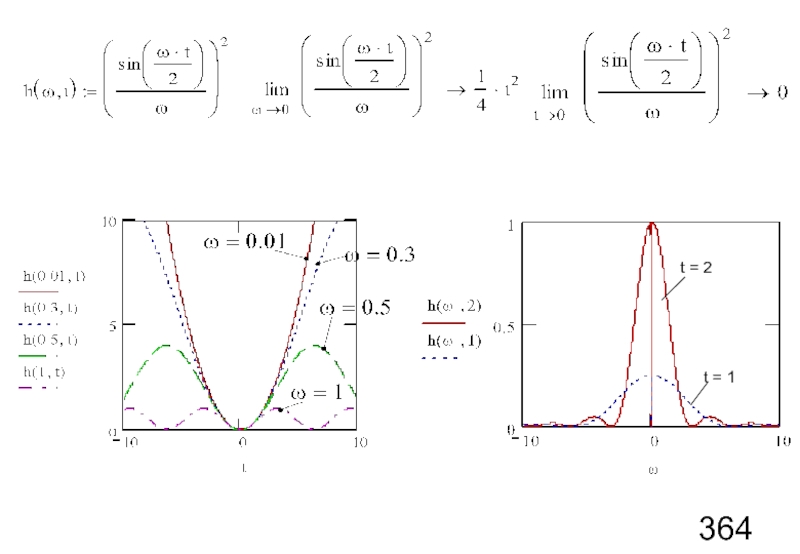
- 83. t = 2 t = 1
- 84. Вывод: Даже если шум «на входе» η(t)
- 85. Предельный случай t → 0
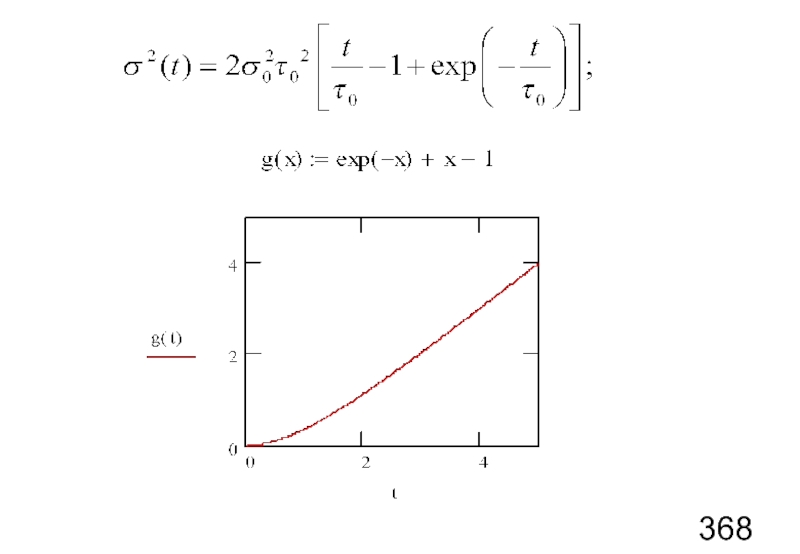
- 86. Конечное время корреляции Символьное вычисление интеграла с помощью MathCad:
- 88. Предельный случай t → ∞
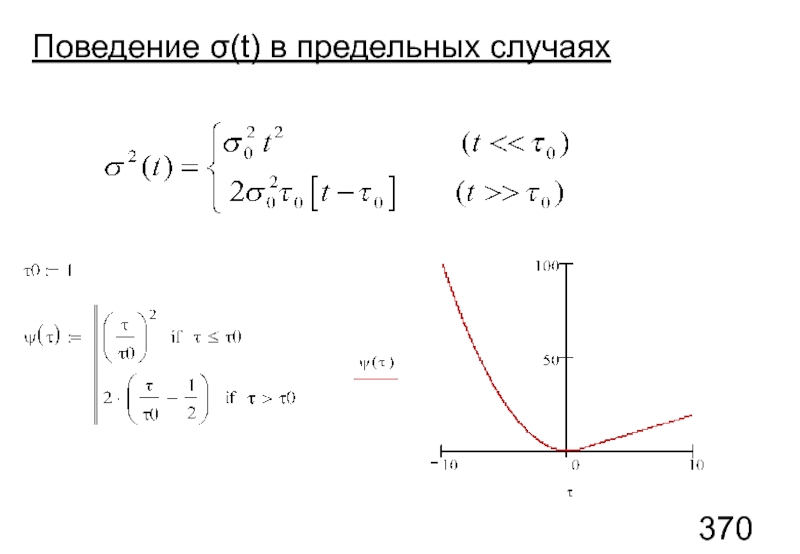
- 89. Поведение σ(t) в предельных случаях
- 90. η(t) - белый шум
- 91. η(t) - белый шум
- 92. η(t) - белый шум
- 93. η(t) - белый шум
- 94. η(t) - белый шум
- 95. η(t) - белый шум Для этого частного
- 96. η(t) - белый шум
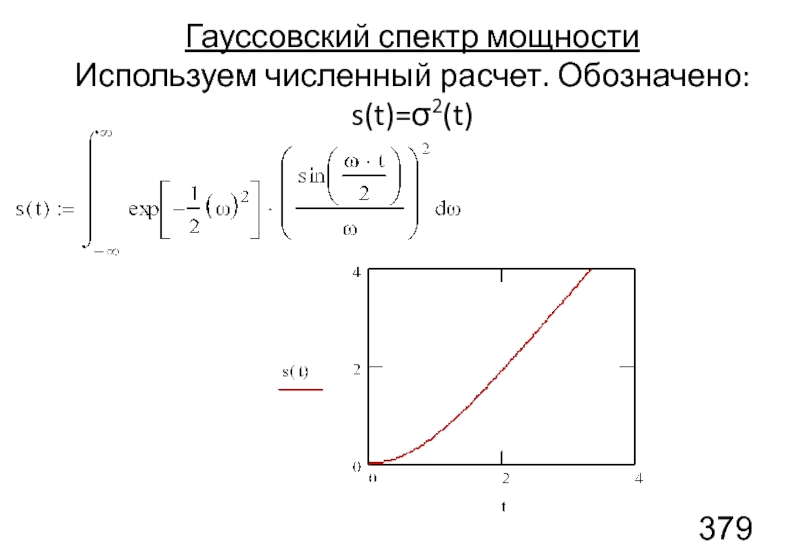
- 97. Гауссовский спектр мощности Используем формулу
- 98. Гауссовский спектр мощности Используем численный расчет. Обозначено: s(t)=σ2(t)
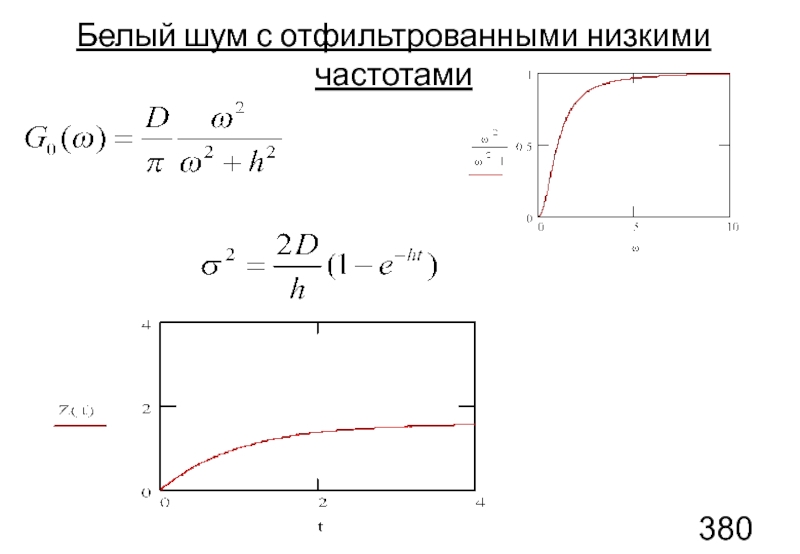
- 99. Белый шум с отфильтрованными низкими частотами
- 100. Фликкер-шум (шум 1 /fγ) Спектр мощности имеет вид:
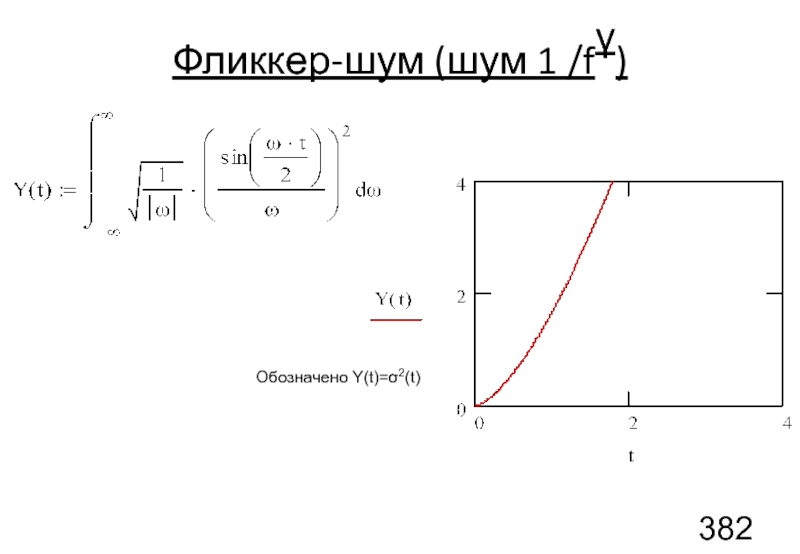
- 101. Фликкер-шум (шум 1 /fγ) Обозначено Y(t)=σ2(t)
- 102. Фликкер-шум (шум 1 /fγ)
- 103. Сводный график зависимости σ2(t) для разных шумов
- 104. Модели случайных процессов (план) см [1].
- 105. Колебания, модулированные шумом. Амплитудная модуляция (АМ) шумом
- 106. Колебания, модулированные шумом. Фазовая модуляция (ФМ) шумом
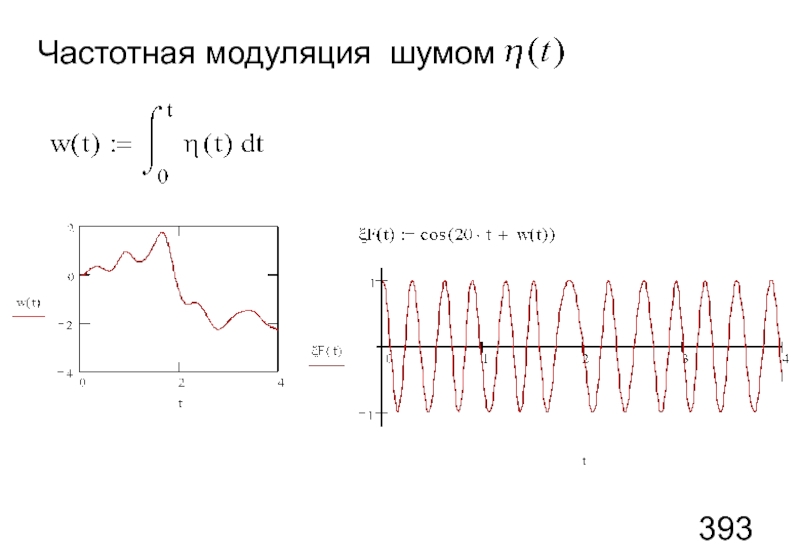
- 107. Колебания, модулированные шумом. Частотная модуляция (ЧМ) шумом
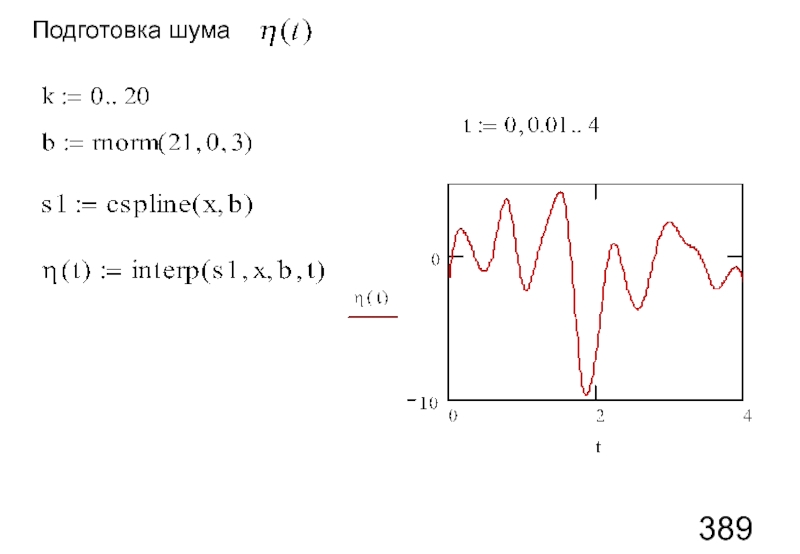
- 108. Подготовка шума
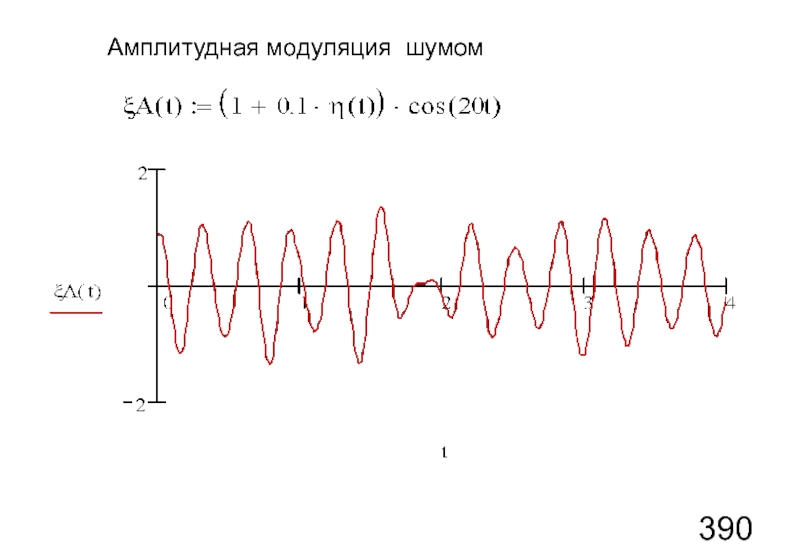
- 109. Амплитудная модуляция шумом
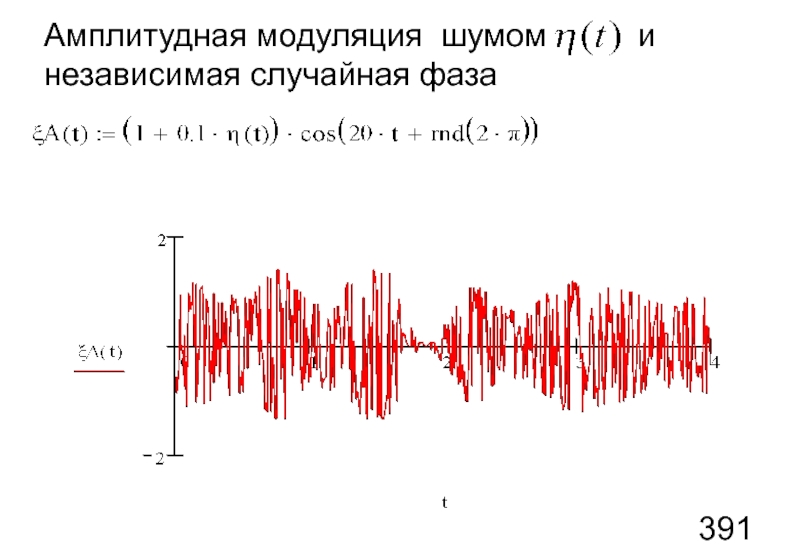
- 110. Амплитудная модуляция шумом и независимая случайная фаза
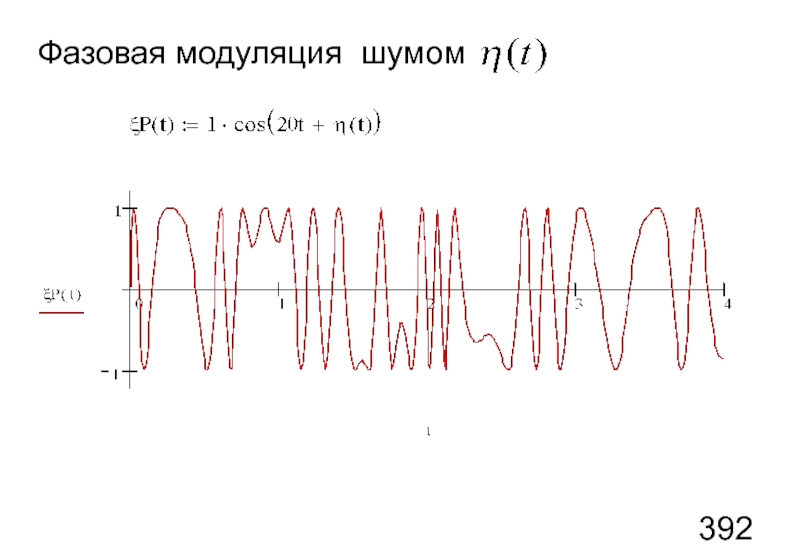
- 111. Фазовая модуляция шумом
- 112. Частотная модуляция шумом
- 113. Найдем среднее от ξ Амплитудная модуляция (АМ) подробно
- 114. Ищем корреляционную функцию процесса ξ Амплитудная модуляция
- 115. Амплитудная модуляция (АМ)
- 116. Перейдем к вычислению спектральной плотности процесса ξ(t) Амплитудная модуляция (АМ) (1) (2) (1)
- 117. Амплитудная модуляция (АМ) (2)
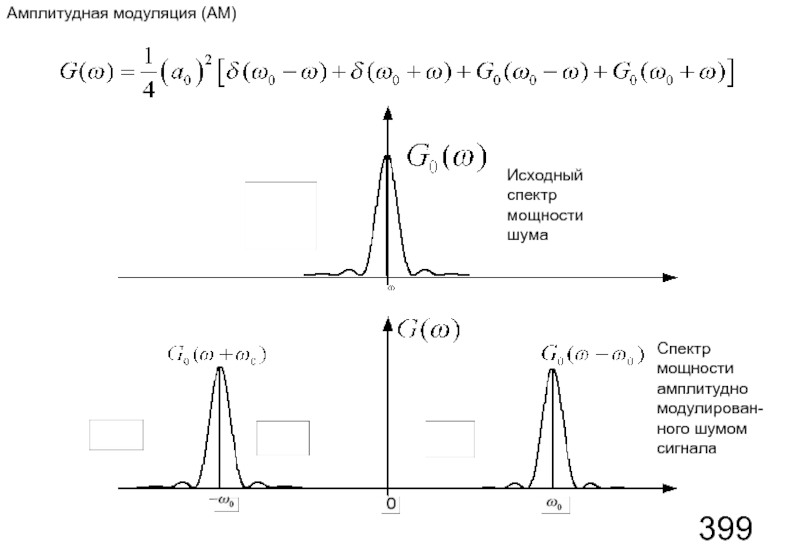
- 118. Исходный спектр мощности шума Спектр мощности амплитудно модулирован- ного шумом сигнала Амплитудная модуляция (АМ)
- 119. Колебания, модулированные шумом Фазовая модуляция (ФМ) гауссовским
- 120. Фазовая модуляция (ФМ) гауссовским шумом Задача состоит в том, чтобы найти статистические характеристики сигнала x(t)
- 121. Для усреднения функции двух переменных ϕ(t) и
- 122. Введем флуктуационную компоненту фазово-модулированного сигнала: Таким
- 123. Зависимость от времени периодическая. Проведем также усреднение
- 124. Фазовая модуляция (ФМ)
- 125. Мы видим, что спектр состоит из непрерывной
- 127. При слабой модуляции сигнала:
- 128. Колебания, модулированные шумом Частотная модуляция (ЧМ)-1 Т.о.,
- 129. Частотная модуляция (ЧМ)-2 Зададим свойства шума η(t):
- 130. Частотная модуляция (ЧМ)-3 Как мы знаем из
- 131. Частотная модуляция (ЧМ)-4 В дальнейшем считаем шум
- 132. Частотная модуляция (ЧМ)-5 Ниже используем аппроксимирующую функцию
- 133. Частотная модуляция (ЧМ)-6 Приближенная функция модулированного сигнала
- 134. Частотная модуляция (ЧМ)-7 Спектр мощности модулированного сигнала
- 135. Спектр мощности модулированного сигнала 2) Слабый
- 136. Спектр мощности модулированного сигнала 3) Слабый
- 137. Частотная модуляция (ЧМ)-10 Интерпретация полученных результатов При
Слайд 2Общий план курса
Случайные процессы и методы их описания.
Модели случайных процессов.
Шумовые колебания
Шумовые колебания в нелинейных системах.
Фильтры.
Основы теории передачи информации по каналам связи
Слайд 3Модели случайных процессов (план)
см [1]. Глава 2
Спектральный анализ сигналов
Гауссовский случайный процесс
Узкополосный
Узкополосный гауссовский шум
Узкополосный негауссовский шум
Диффузионный (винеровский) процесс
Колебания, модулированные шумом
- амплитудная модуляция
- фазовая модуляция
- частотная модуляция
Импульсные случайные процессы
Слайд 4Спектральный анализ сигналов
Периодические сигналы
Где ω - круговая частота, n - любое
Слайд 23Модели случайных процессов (план)
см [1]. Глава 2
Спектральный анализ сигналов
Гауссовский случайный
Узкополосный стационарный шум
Узкополосный гауссовский шум
Узкополосный негауссовский шум
Диффузионный (винеровский) процесс
Колебания, модулированные шумом
- амплитудная модуляция
- фазовая модуляция
- частотная модуляция
Импульсные случайные процессы
Слайд 24Гауссовский случайный процесс
Многомерная гауссовская плотность вероятности
Смысл параметров гауссовской плотности вероятности:
Слайд 26Гауссовский случайный процесс-3
Одномерная плотность вероятности примет вид:
В этой формуле все параметры
Слайд 27Гауссовский случайный процесс-4
Свойства одномерного распределения.
Отличны от нуля лишь четные центральные моменты
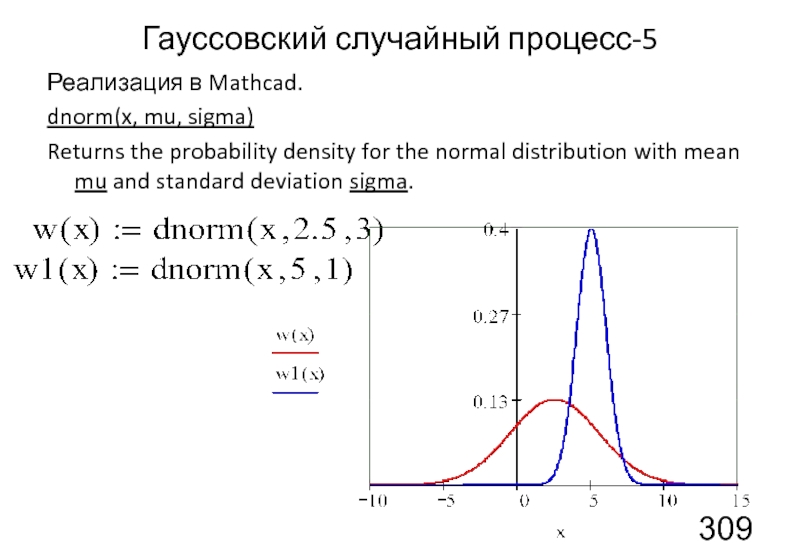
Слайд 28Гауссовский случайный процесс-5
Реализация в Mathcad.
dnorm(x, mu, sigma)
Returns the probability density
Слайд 32Гауссовский случайный процесс-9
Для вычисления корреляционного момента достаточно парной (для 2-х переменных)
Наша цель – выразить все параметры через экспериментально измеримые данные
Слайд 34Гауссовский процесс-11
Таким образом, плотность вероятности может быть выражена через экспериментально измеримые
Рассмотрим применение распределения для описания случайных процессов
Слайд 37Гауссовский случайный процесс-14
Выводы:
1. Если процесс гауссовский, то все его характеристики можно
2. Для стационарного гауссовского процесса параметры μ и β не зависят от времени.
Слайд 38Модели случайных процессов (план)
см [1]. Глава 2
Спектральный анализ сигналов
Гауссовский
Узкополосный стационарный шум
Узкополосный гауссовский шум
Узкополосный негауссовский шум
Диффузионный (винеровский) процесс
Колебания, модулированные шумом
- амплитудная модуляция
- фазовая модуляция
- частотная модуляция
Импульсные случайные процессы
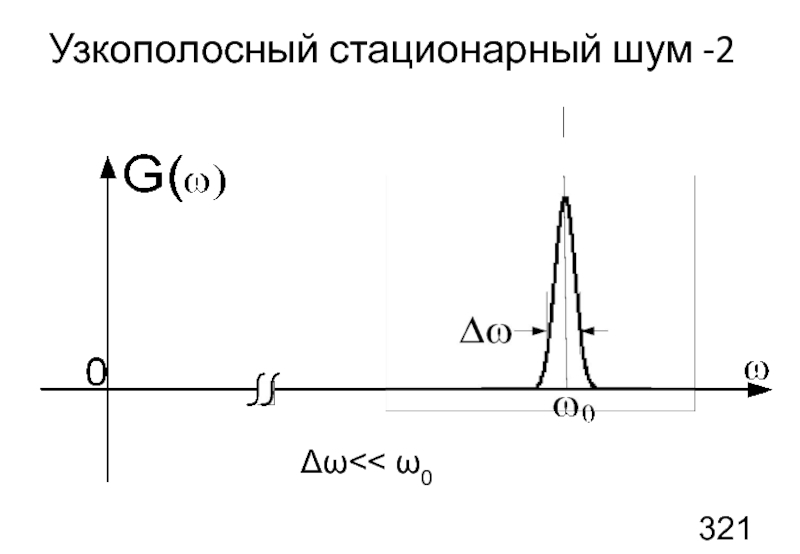
Слайд 39Узкополосный стационарный шум
Шум узкополосный, если спектральная плотность G(ω) отлична от нуля
Δω<< ω0
в виде колебаний, близких к гармоническим
Слайд 41Узкополосный стационарный шум -2
Флуктуационную компоненту представим в виде (модель узкополосного шума):
где
ρ(t) – огибающая (амплитуда).
ϕ(t) – фаза.
Слайд 42Вместо огибающей и фазы также вводят квадратурные компоненты a(t), b(t)
Таким образом,
быстрые
медленные a(t), b(t) или ρ(t), ϕ(t)
Слайд 44Пример реализации узкополосного шума-2
Сгладим полученные случайные зависимости, используя кубическую интерполяцию
Слайд 45Пример реализации узкополосного шума-3
Скомбинируем модельную узкополосную случайную функцию и построим несколько
Слайд 46Постановка задачи:
Задача: зная свойства шума ξ(t) найти статистические характеристики огибающей и
Все рассматриваемые случайные процессы
Сам шум
Его амплитуда и фаза
Квадратурные компоненты
Считаются стационарными случайными функциями времени.
Слайд 47Корреляционные и спектральные характеристики квадратурных компонент
Предполагаем, что
Так как
то
Переходим к анализу корреляционной функции
Слайд 48Считаем известной корреляционную функцию
Подставим в эту формулу представление
Слайд 49Учтем известные тригонометрические формулы
Подставим эти выражения в приведенное выше выражение
Слайд 50В силу стационарности здесь не должно быть явной зависимости от времени,
Это следует из равноправности амплитуд
Здесь и некоторые пока неизвестные функции.
1)
2)
Чётная функция аргумента τ
Нечётная функция аргумента τ
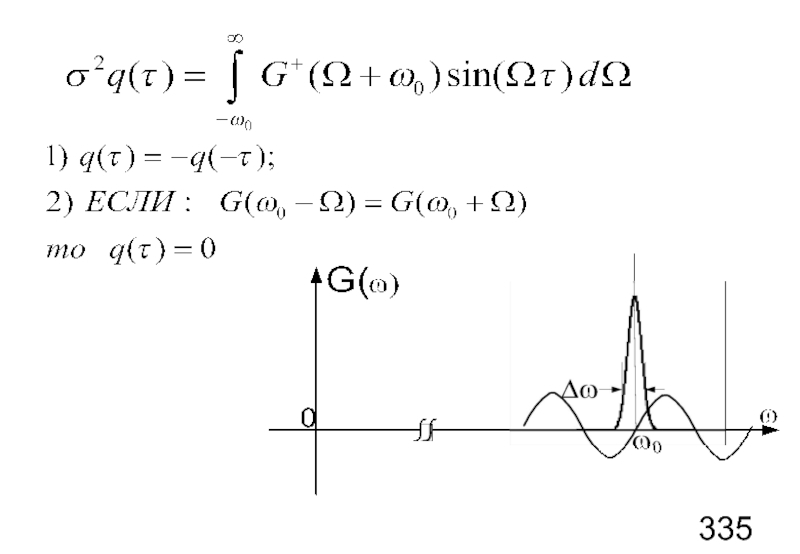
Слайд 52Чтобы найти неизвестные функции
воспользуемся формулой Винера-Хинчина:
Интеграл от нечетной функции (содержит
Сдвиг начала координат в точку ω0.
Слайд 56Модели случайных процессов (план)
см [1]. Глава 2
Спектральный анализ сигналов
Гауссовский
Узкополосный стационарный шум
Узкополосный гауссовский шум
Узкополосный негауссовский шум
Диффузионный (винеровский) процесс
Колебания, модулированные шумом
- амплитудная модуляция
- фазовая модуляция
- частотная модуляция
Импульсные случайные процессы
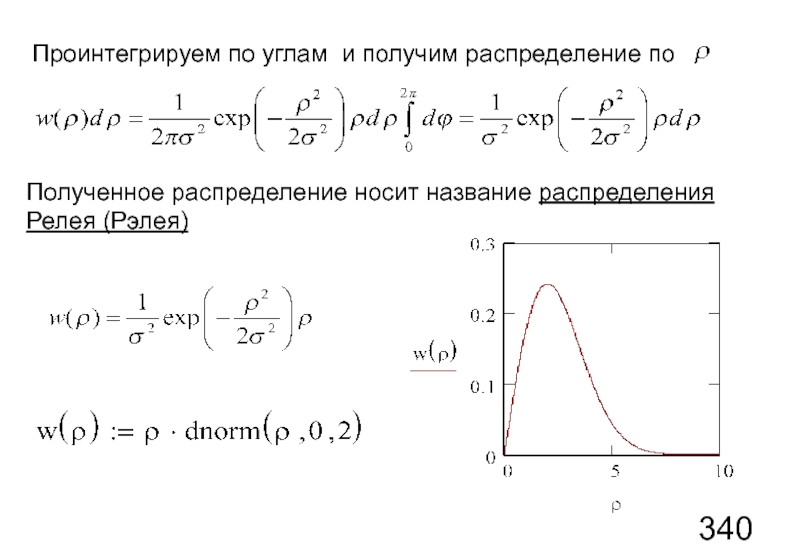
Слайд 59Проинтегрируем по углам и получим распределение по
Полученное распределение носит название
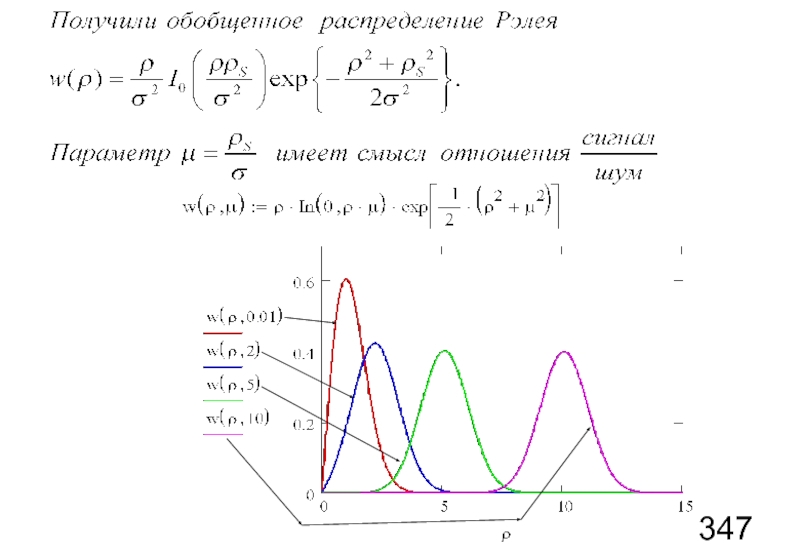
Слайд 61Используем полученные результаты для анализа суперпозиции гармонического сигнала и гауссовского шума.
Случайный
Слайд 62Будем искать вероятностные характеристики огибающей и фазы,
Исходим из распределения квадратурных компонент шума:
Так как
якобиан имеет прежний вид
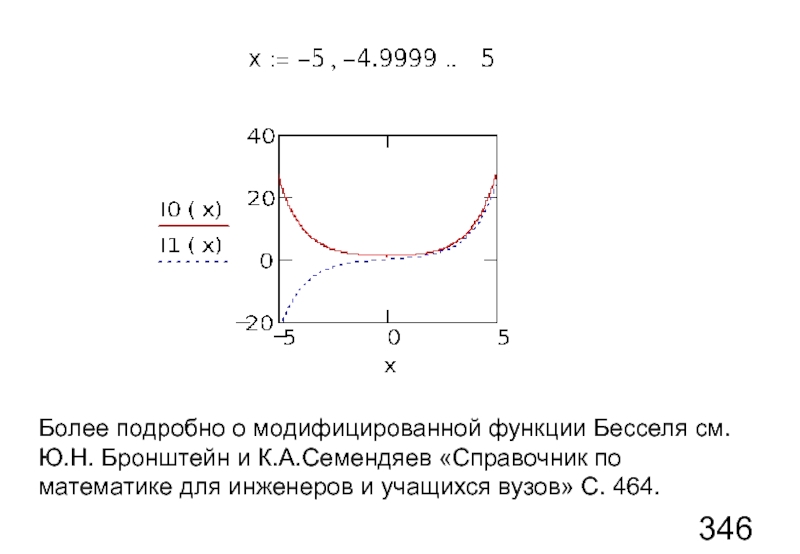
Слайд 65Более подробно о модифицированной функции Бесселя см. Ю.Н. Бронштейн и К.А.Семендяев
Слайд 67Замечание об использовании Mathcad.
В Mathcad имеется специальная функция
Returns the m-th
Именно этот оператор использовался выше.
Слайд 71Построение графика W(φ,μ) средствами Mathcad
где использована специальная функция (Function Category -
erf(z)
Returns the error function.
,
Слайд 73
Модели случайных процессов (план)
см [1]. Глава 2
Спектральный анализ сигналов
Гауссовский
Узкополосный стационарный шум
Узкополосный гауссовский шум
Узкополосный негауссовский шум (ознакомиться самостоятельно!)
Диффузионный (винеровский) процесс
Колебания, модулированные шумом
- амплитудная модуляция
- фазовая модуляция
- частотная модуляция
Импульсные случайные процессы
Слайд 76Постановка задачи:
найти вероятностные свойства процесса ξ(t), зная свойства процесса η(t).
Пусть
Требуется найти:
Слайд 84Вывод:
Даже если шум «на входе» η(t) стационарный, винеровский процесс ξ(t) «на
нестационарный:
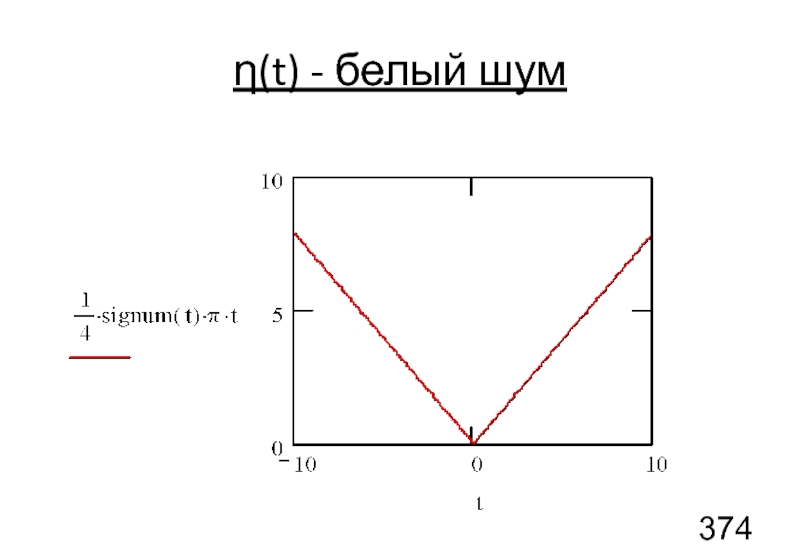
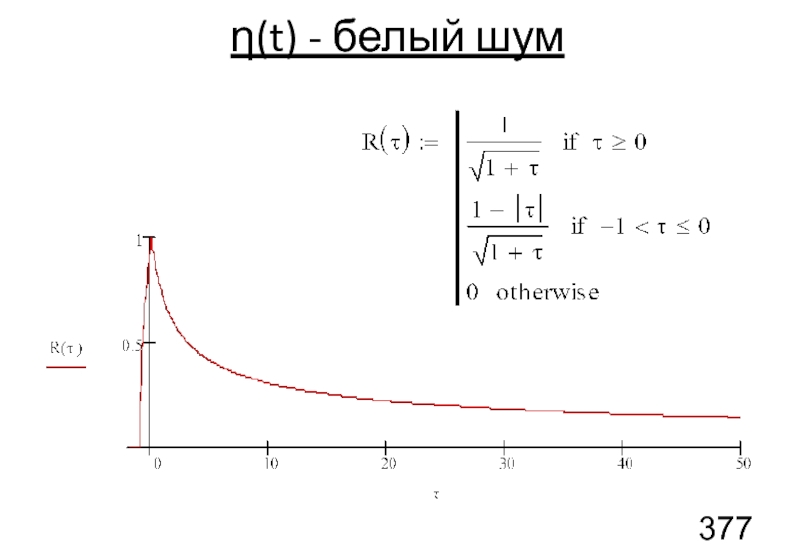
Слайд 95η(t) - белый шум
Для этого частного случая можно также вычислить корреляционную
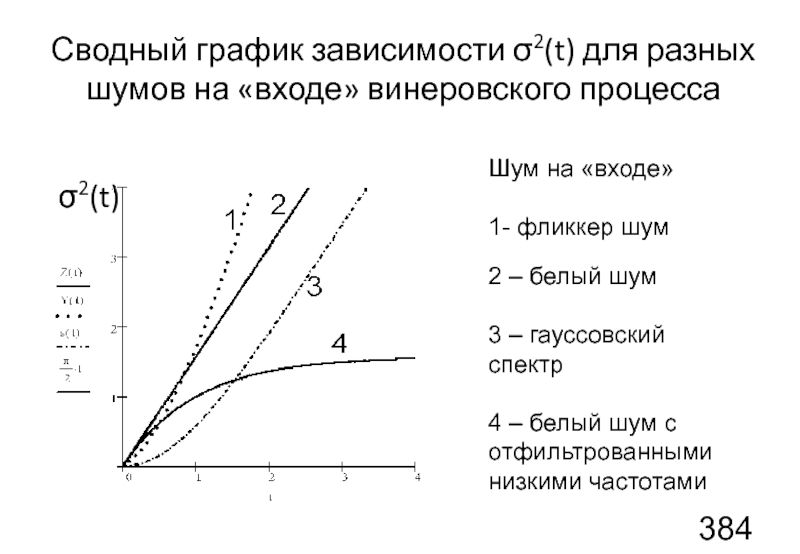
Слайд 103Сводный график зависимости σ2(t) для разных шумов на «входе» винеровского процесса
Шум
1- фликкер шум
2 – белый шум
3 – гауссовский
спектр
4 – белый шум с отфильтрованными низкими частотами
σ2(t)
Слайд 104
Модели случайных процессов (план) см [1]. Глава 2
Спектральный анализ сигналов
Узкополосный стационарный шум
Узкополосный гауссовский шум
Узкополосный негауссовский шум (ознакомиться самостоятельно!)
Диффузионный (винеровский) процесс
Колебания, модулированные шумом
- амплитудная модуляция
- фазовая модуляция
- частотная модуляция
Импульсные случайные процессы
Слайд 105Колебания, модулированные шумом.
Амплитудная модуляция (АМ) шумом
Amplitude - амплитуда
Постановка задачи:
Задан шум
Постановка
Слайд 106Колебания, модулированные шумом.
Фазовая модуляция (ФМ) шумом
Phase – фаза
Постановка задачи:
Задан шум
Постановка
Слайд 107Колебания, модулированные шумом.
Частотная модуляция (ЧМ) шумом
Frequency - частота
Постановка задачи:
Задан шум
Постановка
Слайд 114Ищем корреляционную функцию процесса ξ
Амплитудная модуляция (АМ)
Здесь подразумевается усреднение по случайной
Слайд 116Перейдем к вычислению спектральной плотности процесса ξ(t)
Амплитудная модуляция (АМ)
(1)
(2)
(1)
Слайд 118Исходный спектр мощности шума
Спектр мощности
амплитудно модулирован- ного шумом сигнала
Амплитудная модуляция (АМ)
Слайд 119Колебания, модулированные шумом
Фазовая модуляция (ФМ) гауссовским шумом
Предположим, что
Слайд 120Фазовая модуляция (ФМ) гауссовским шумом Задача состоит в том, чтобы найти статистические
Слайд 121Для усреднения функции двух переменных ϕ(t) и ϕ(t+τ) также используем распределение
Фазовая модуляция (ФМ)
Слайд 122Введем флуктуационную компоненту фазово-модулированного сигнала:
Таким образом, фазово-модулированный сигнал оказывается нестационарным
Фазовая модуляция (ФМ)
Слайд 123Зависимость от времени периодическая. Проведем также усреднение всех величин по периоду
Фазовая модуляция (ФМ)
Слайд 125Мы видим, что спектр состоит из непрерывной компоненты и двух дискретных
Дискретные
Непрерывная компонента
Введем интегральную интенсивность спектра
Фазовая модуляция (ФМ)
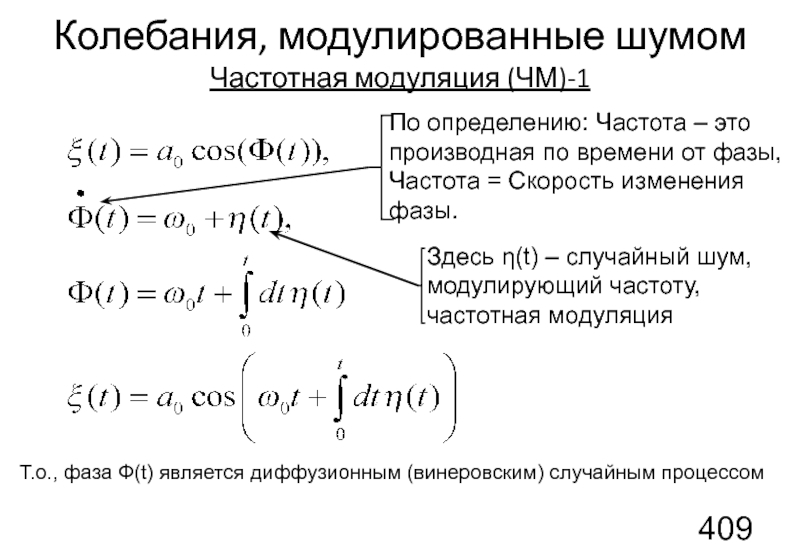
Слайд 128Колебания, модулированные шумом
Частотная модуляция (ЧМ)-1
Т.о., фаза Ф(t) является диффузионным (винеровским) случайным
Здесь η(t) – случайный шум, модулирующий частоту, частотная модуляция
По определению: Частота – это производная по времени от фазы, Частота = Скорость изменения фазы.
Слайд 129Частотная модуляция (ЧМ)-2
Зададим свойства шума η(t):
1) шум считаем стационарным;
2)
Наша задача: исследовать
1) фазы
2) самого колебания ξ(t).
Слайд 130Частотная модуляция (ЧМ)-3
Как мы знаем из свойств диффузионного процесса (см. выше,
Слайд 131Частотная модуляция (ЧМ)-4
В дальнейшем считаем шум η(t) гауссовским.
Используя полученные выше
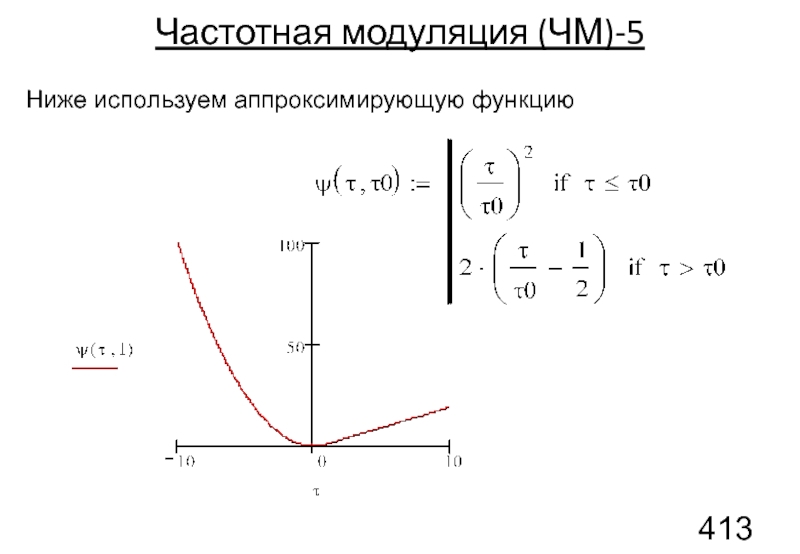
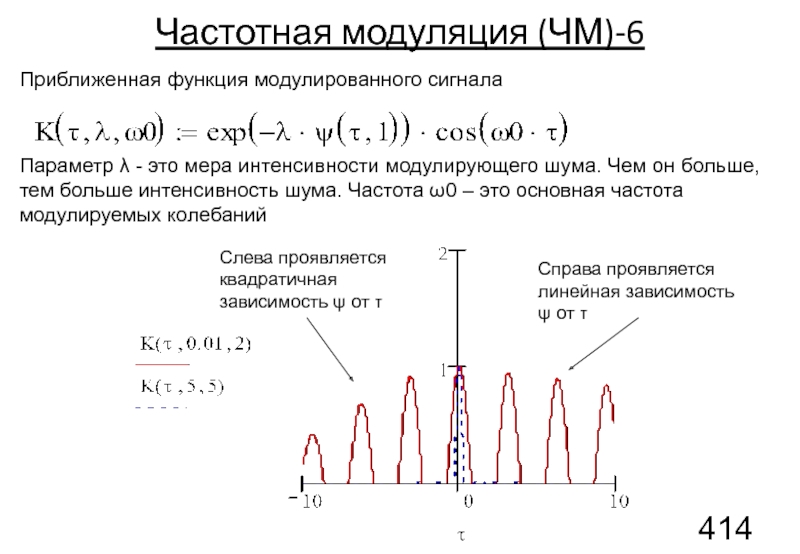
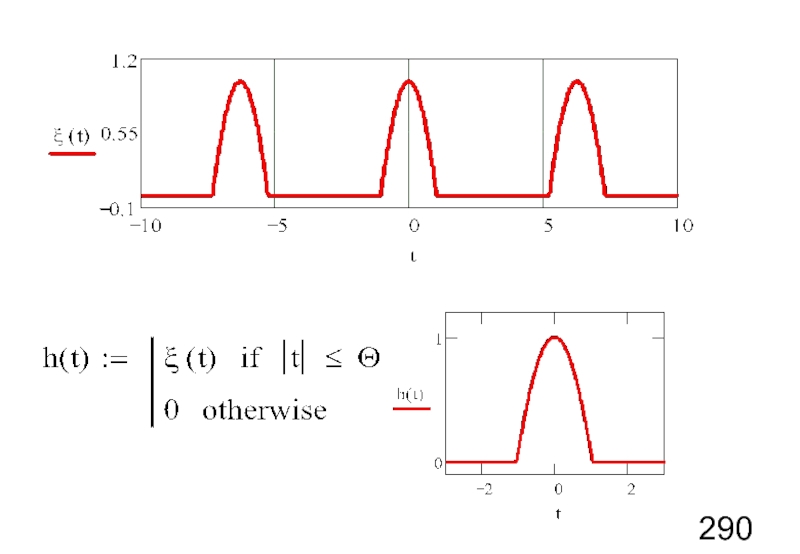
Слайд 133Частотная модуляция (ЧМ)-6
Приближенная функция модулированного сигнала
Слева проявляется квадратичная зависимость ψ от
Справа проявляется линейная зависимость ψ от τ
Параметр λ - это мера интенсивности модулирующего шума. Чем он больше, тем больше интенсивность шума. Частота ω0 – это основная частота модулируемых колебаний
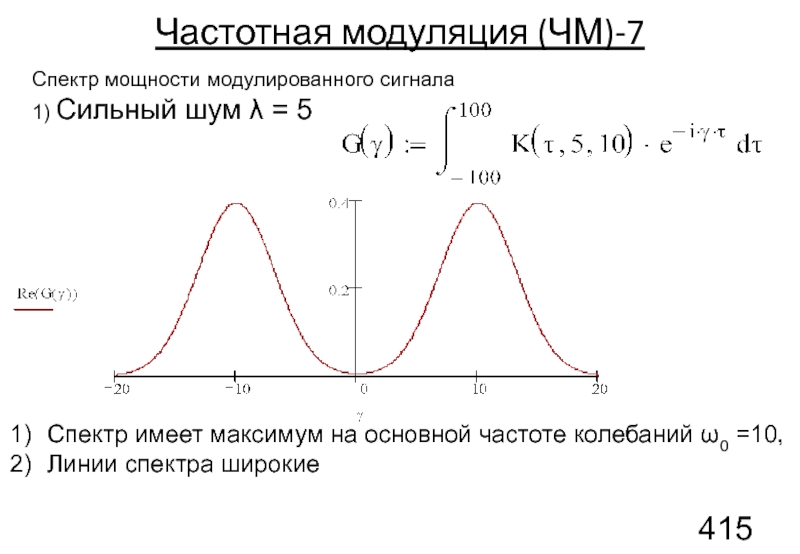
Слайд 134Частотная модуляция (ЧМ)-7
Спектр мощности модулированного сигнала
1) Сильный шум λ =
Спектр имеет максимум на основной частоте колебаний ω0 =10,
Линии спектра широкие
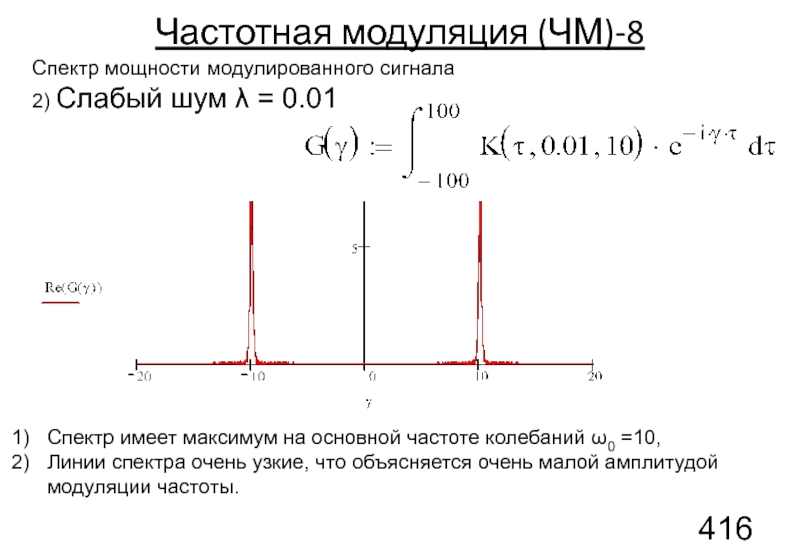
Слайд 135Спектр мощности модулированного сигнала
2) Слабый шум λ = 0.01
Частотная модуляция
Спектр имеет максимум на основной частоте колебаний ω0 =10,
Линии спектра очень узкие, что объясняется очень малой амплитудой модуляции частоты.
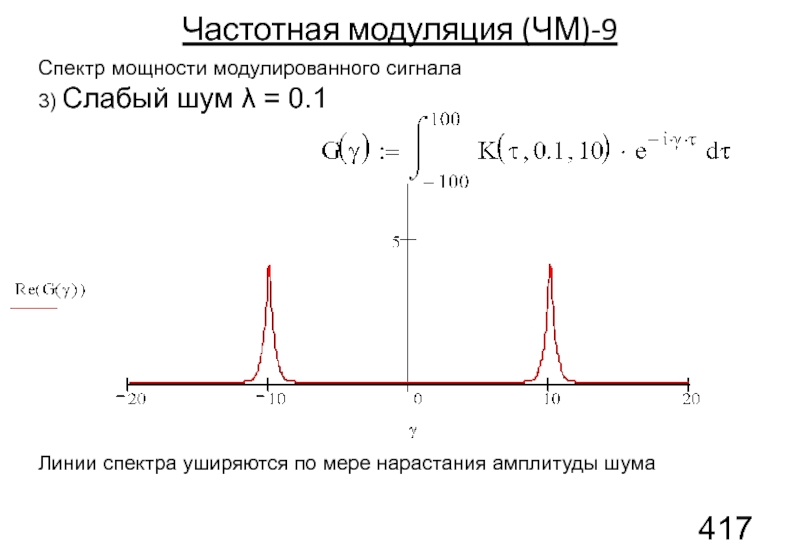
Слайд 136Спектр мощности модулированного сигнала
3) Слабый шум λ = 0.1
Частотная модуляция
Линии спектра уширяются по мере нарастания амплитуды шума
Слайд 137Частотная модуляция (ЧМ)-10
Интерпретация полученных результатов
При большой интенсивности модуляций
в корреляционной функции
2) При малой интенсивности модуляций
в корреляционной функции заменим ψ(τ) на линейную функцию τ и получим лоренцевский спектр


![Модели случайных процессов (план) см [1]. Глава 2Спектральный анализ сигналовГауссовский случайный процессУзкополосный стационарный шумУзкополосный гауссовский](/img/tmb/3/280676/e2d4b913b2fc4a9986a270ae30a04533-800x.jpg)






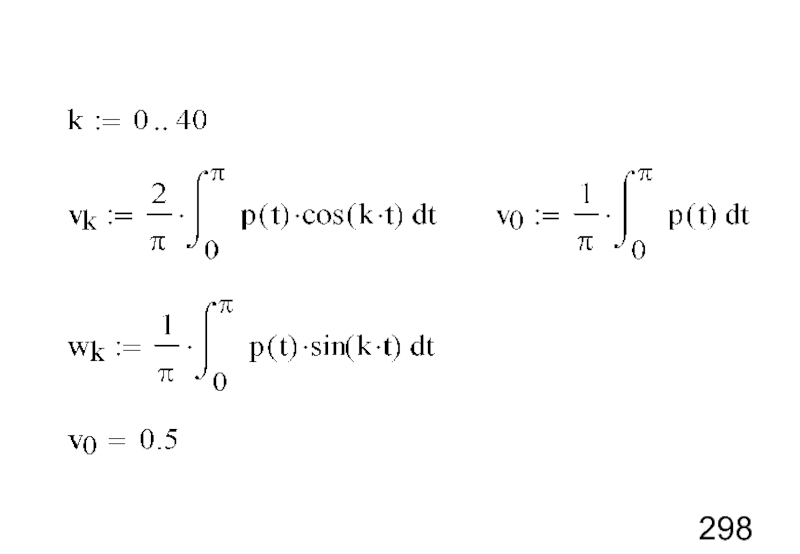
![Модели случайных процессов (план) см [1]. Глава 2 Спектральный анализ сигналовГауссовский случайный процессУзкополосный стационарный шумУзкополосный](/img/tmb/3/280676/7fe68cfd52e6e2662018add2dbe72c3e-800x.jpg)










![Модели случайных процессов (план) см [1]. Глава 2 Спектральный анализ сигналов Гауссовский случайный процессУзкополосный стационарный](/img/tmb/3/280676/41f61ca76136d9851acc2dd02321ace0-800x.jpg)










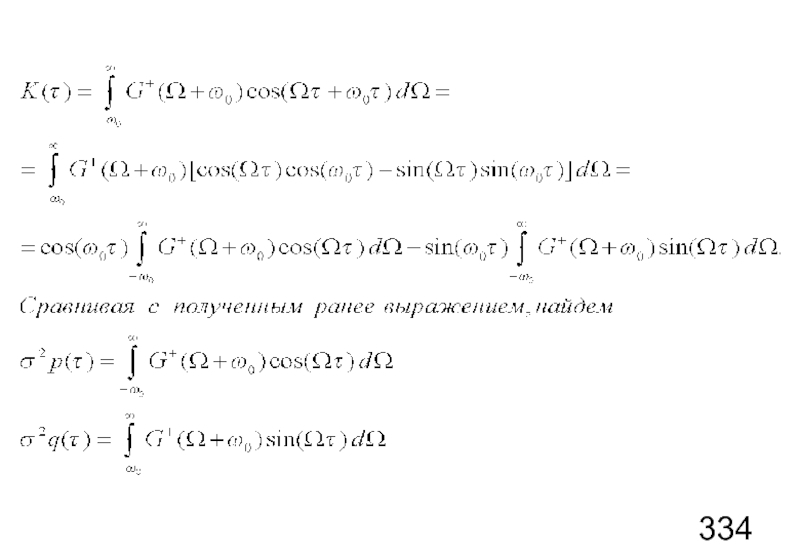

![Модели случайных процессов (план) см [1]. Глава 2 Спектральный анализ сигналов Гауссовский случайный процесс Узкополосный](/img/tmb/3/280676/e74b9cf7eef9cc784097846a207dc87d-800x.jpg)












![Модели случайных процессов (план) см [1]. Глава 2 Спектральный анализ сигналов Гауссовский случайный процесс Узкополосный](/img/tmb/3/280676/6d28bc040e853c41172047a4446df29d-800x.jpg)
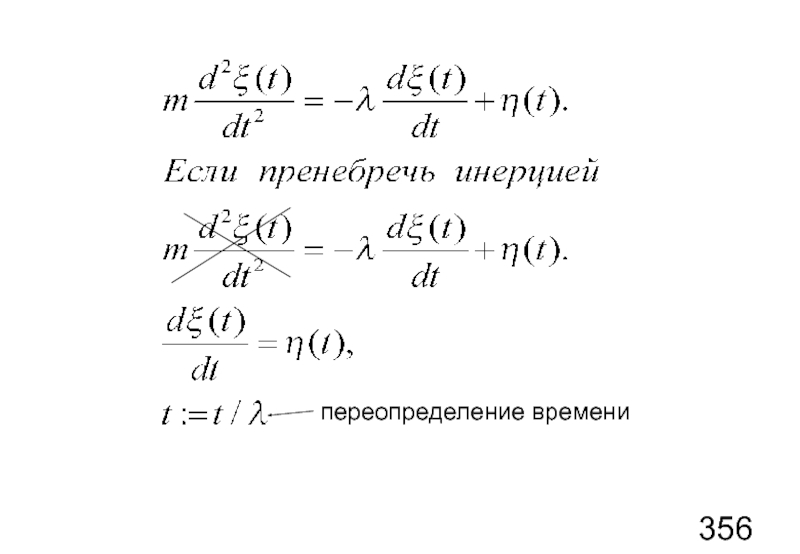

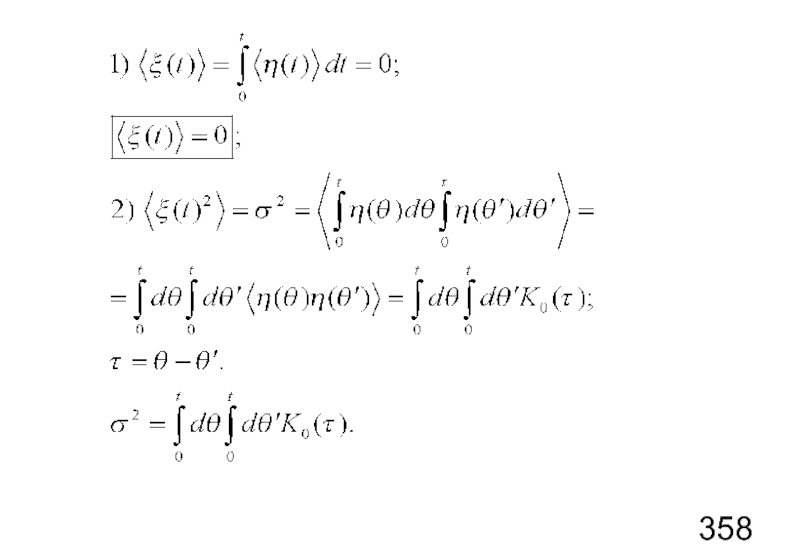
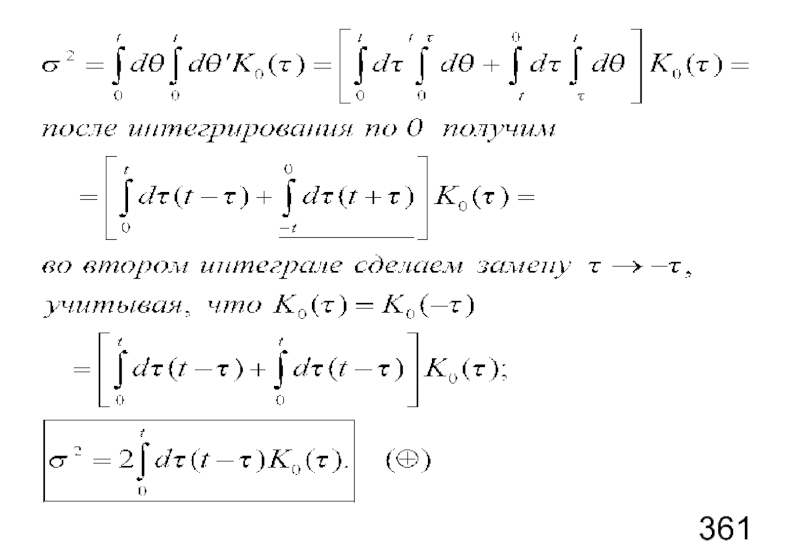




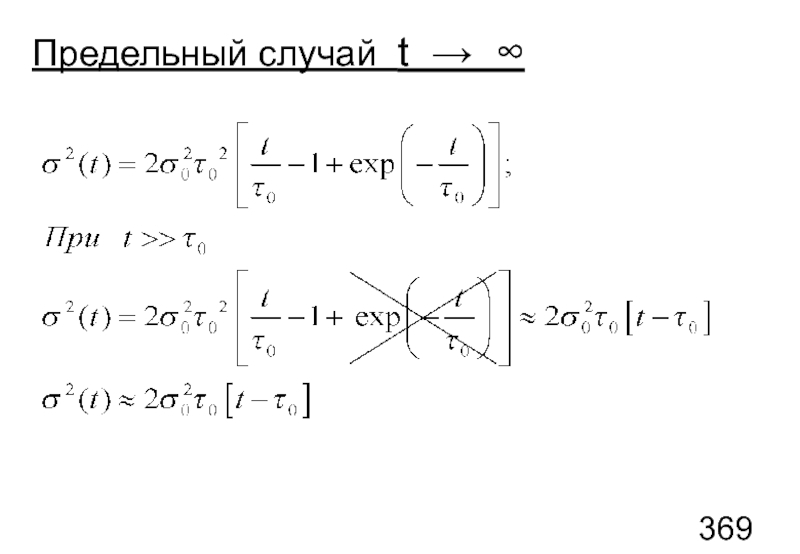








![Модели случайных процессов (план) см [1]. Глава 2 Спектральный анализ сигналов Гауссовский случайный процесс Узкополосный](/img/tmb/3/280676/f66e8a940d0cde59d578ed512e103257-800x.jpg)