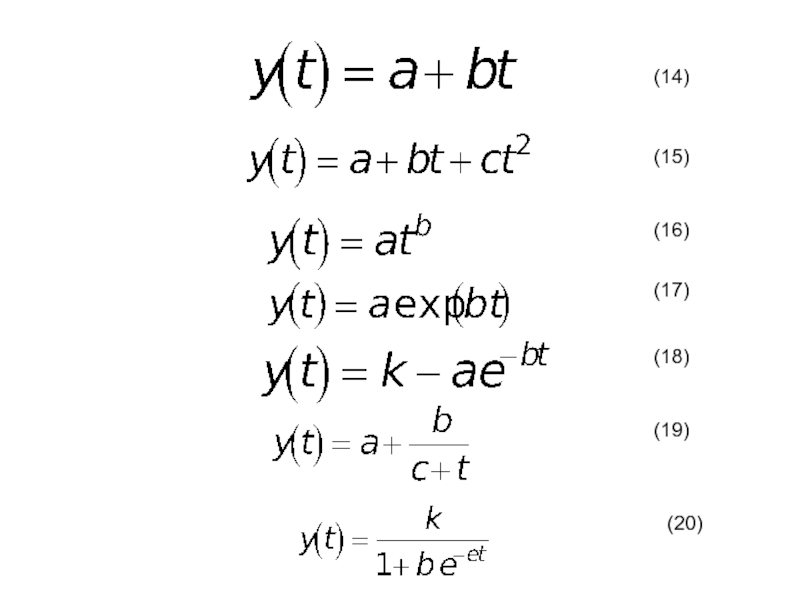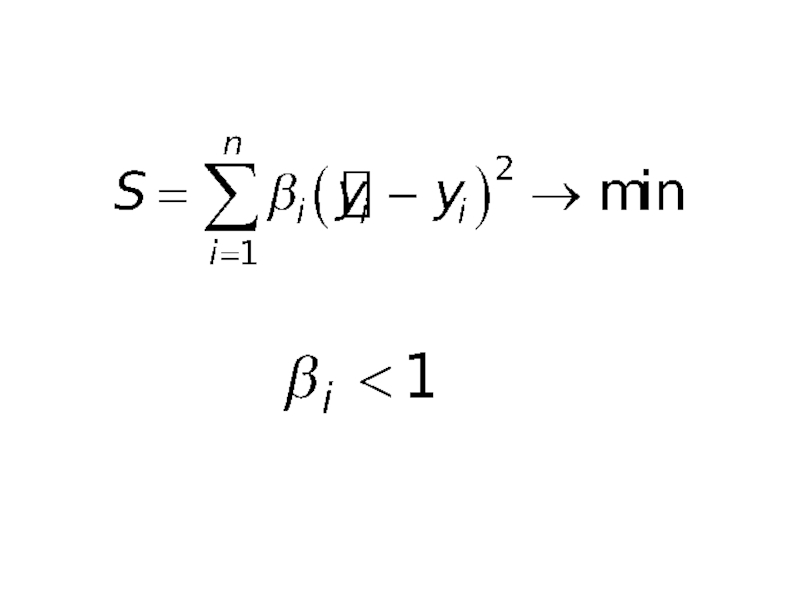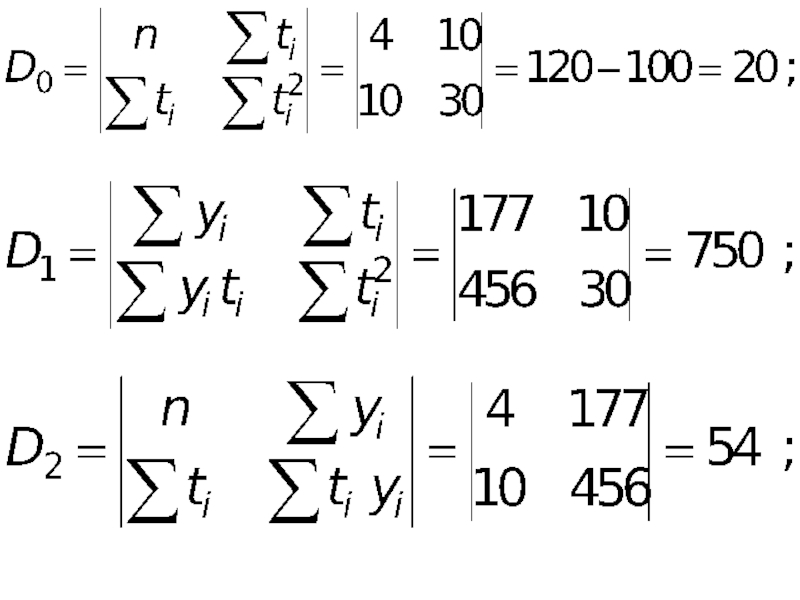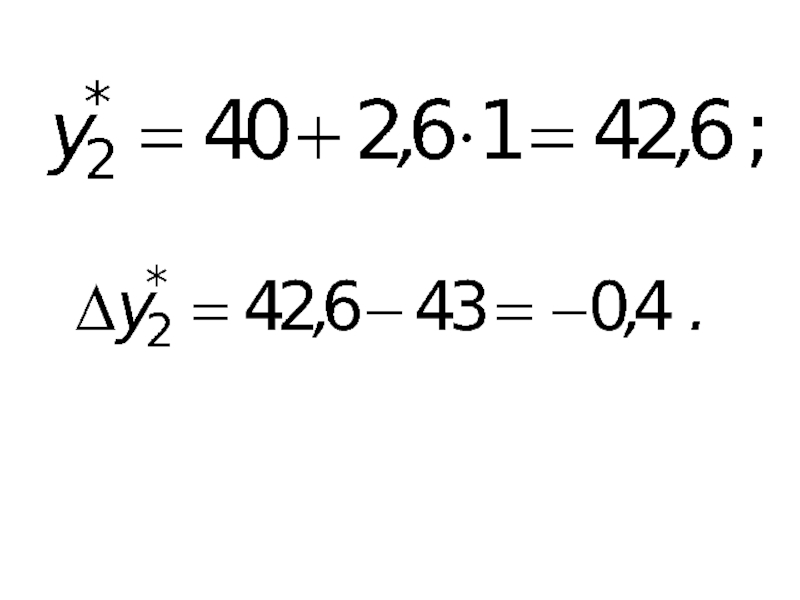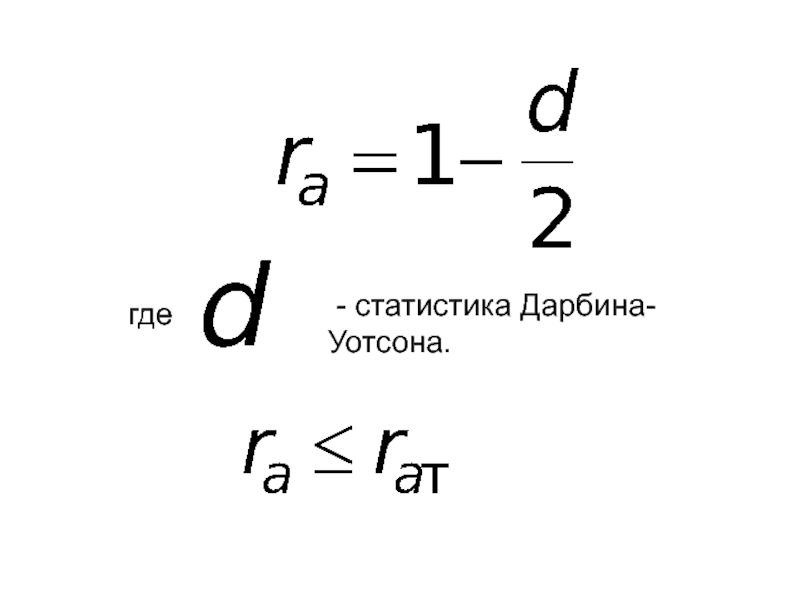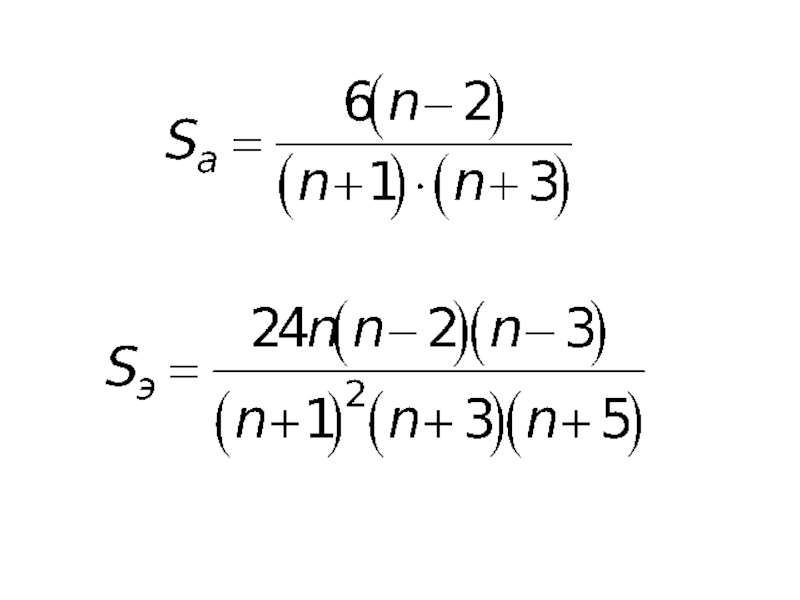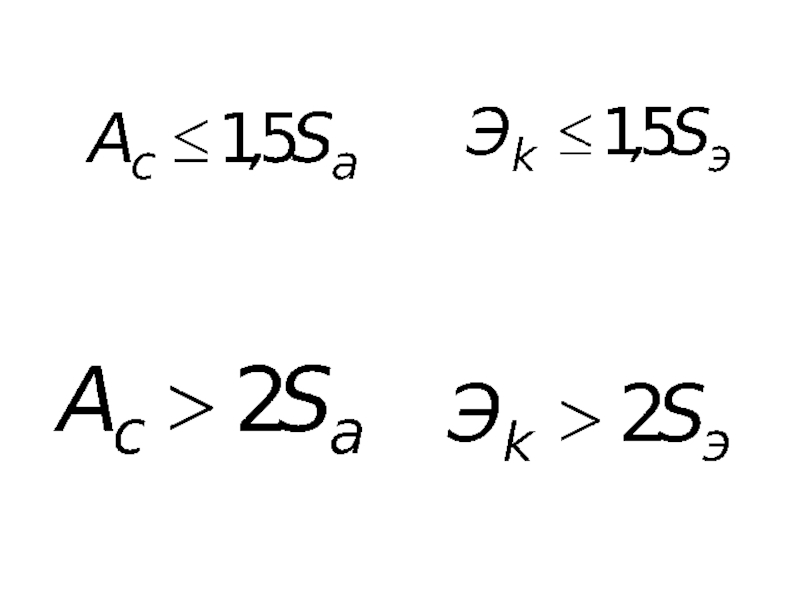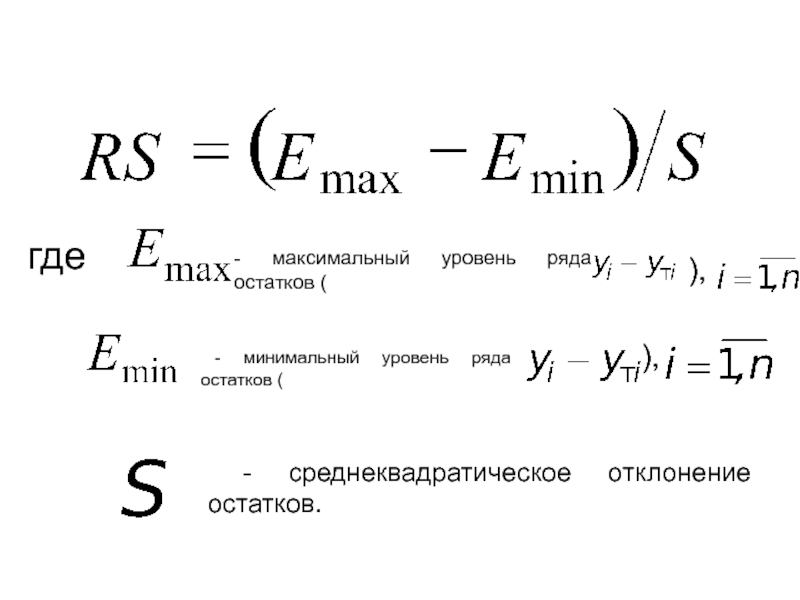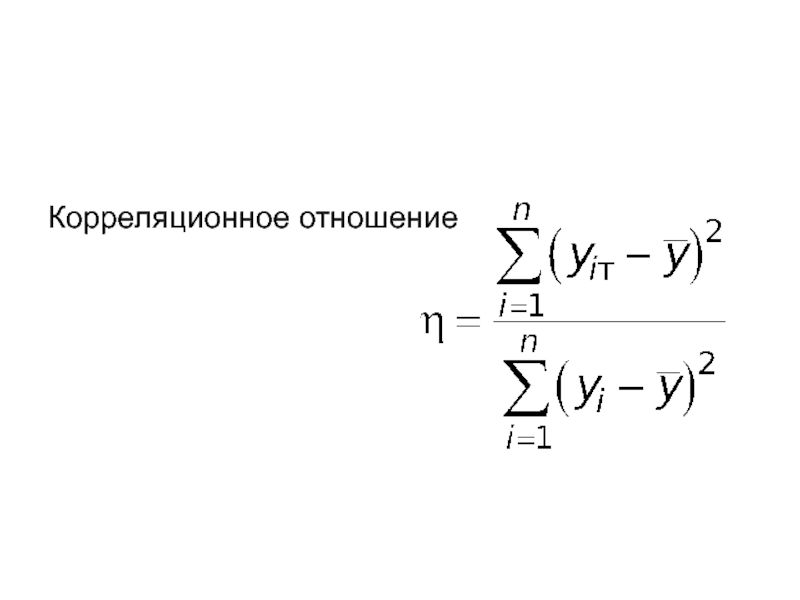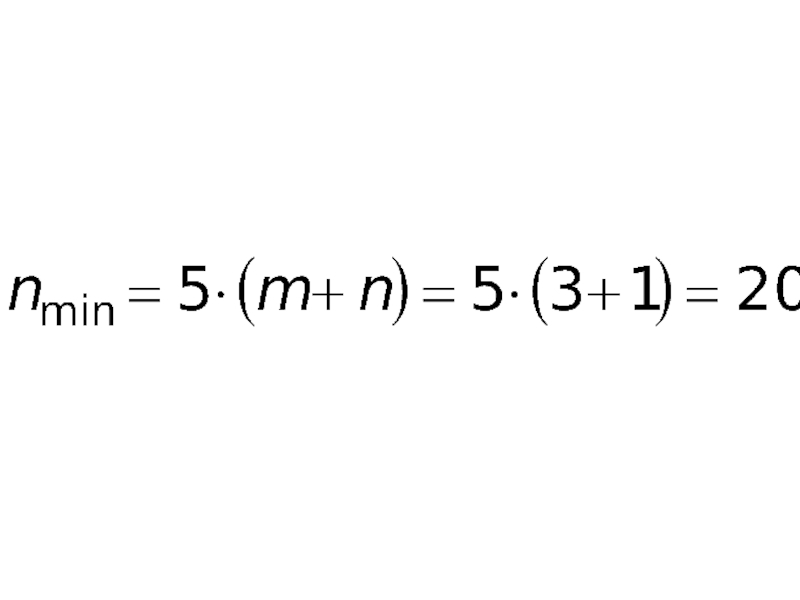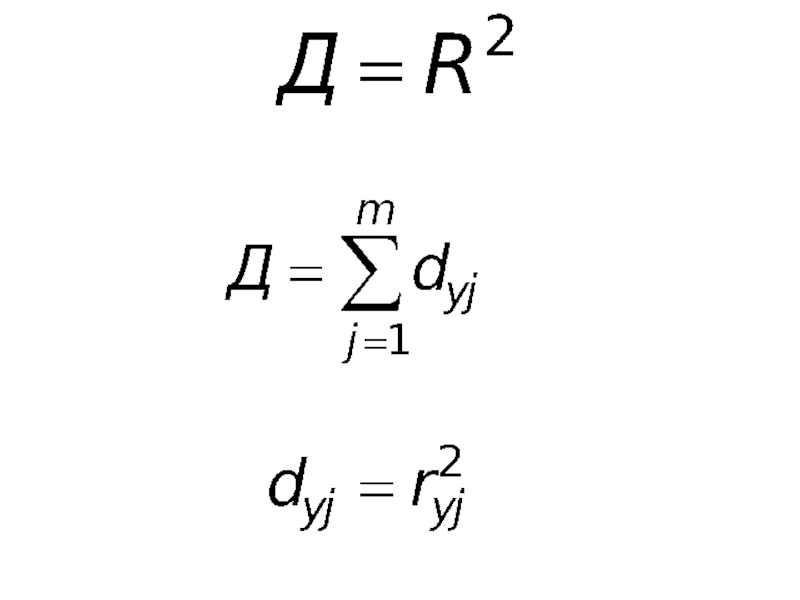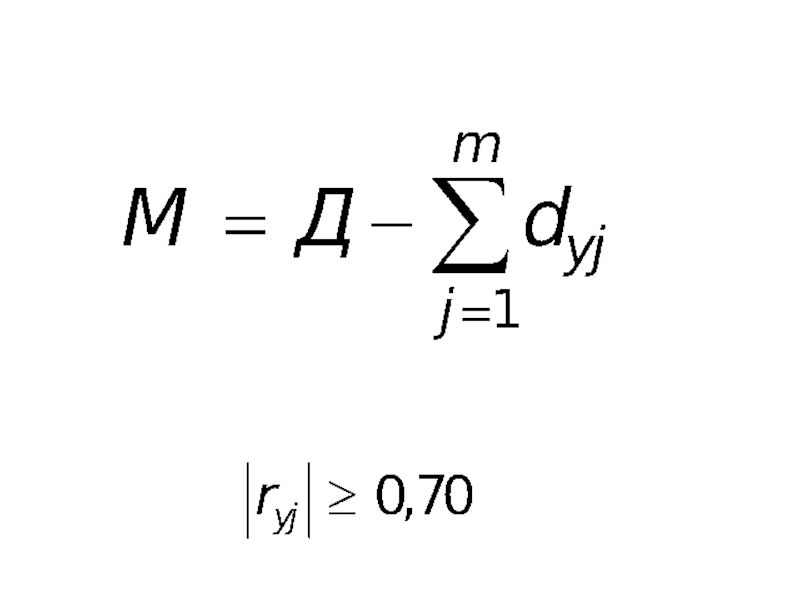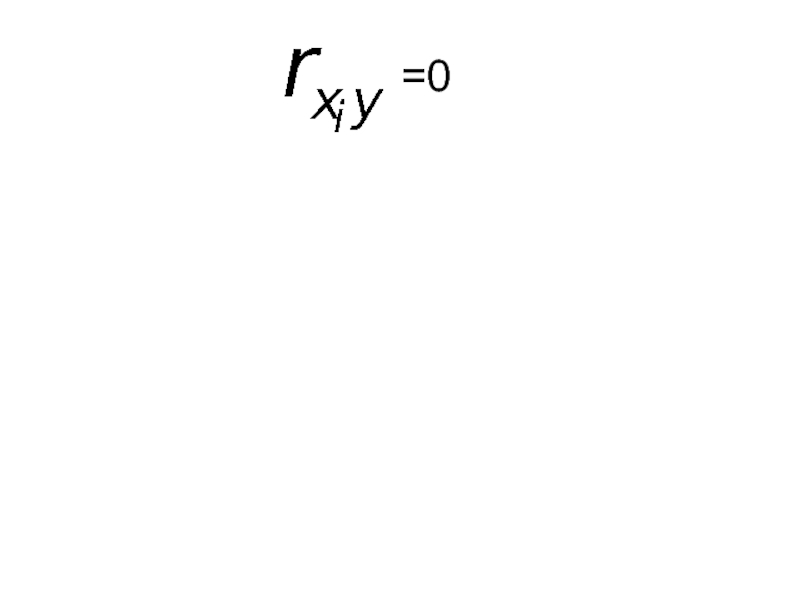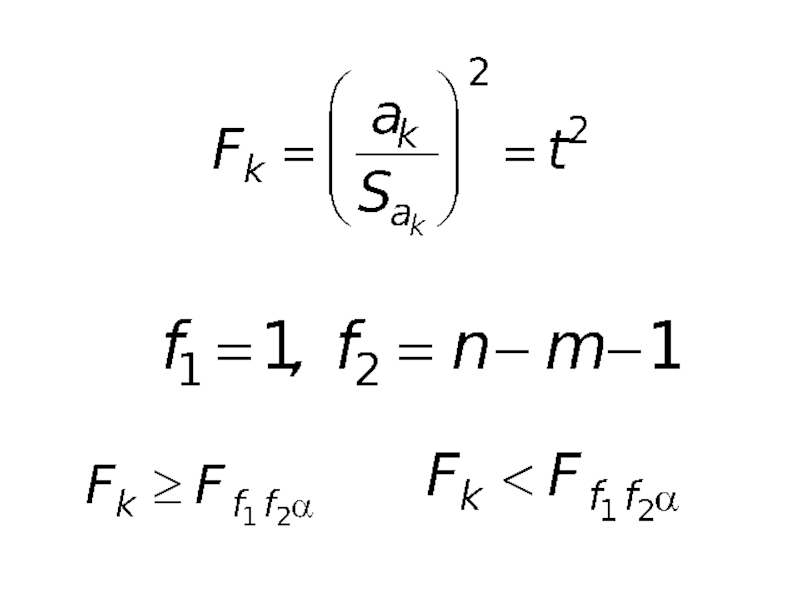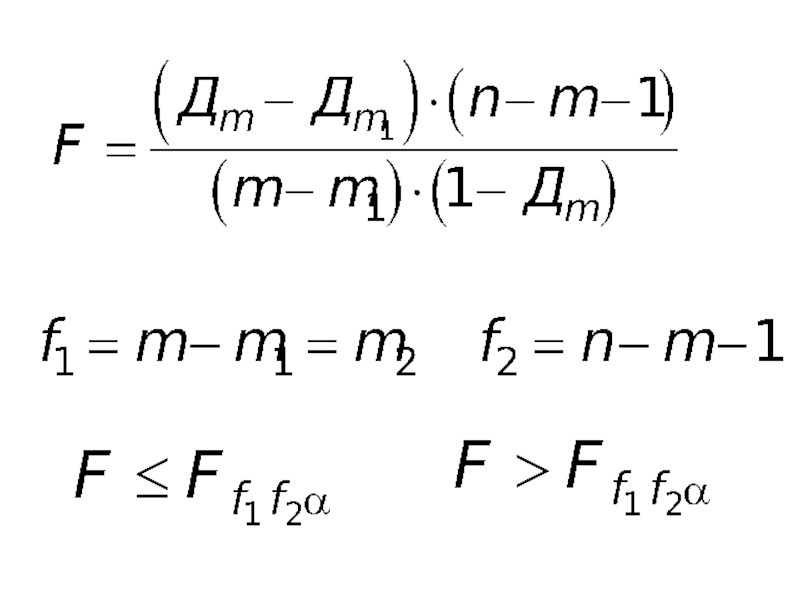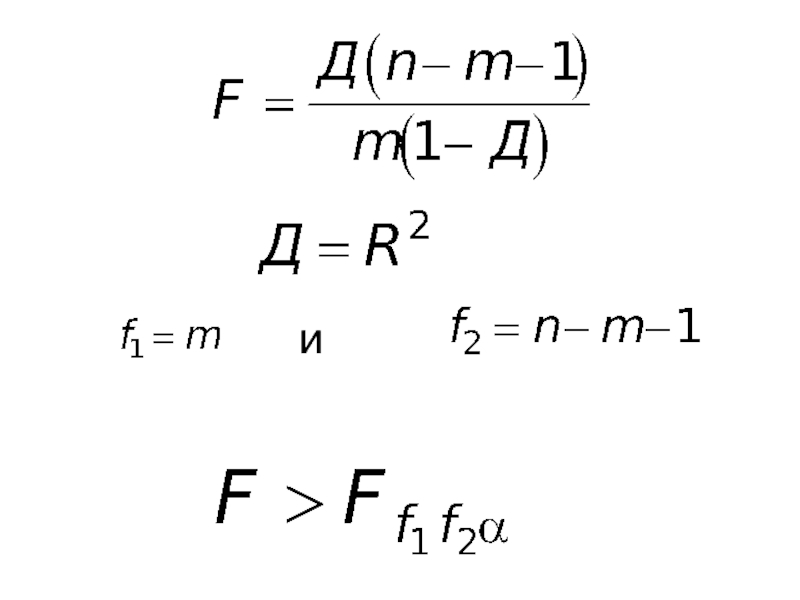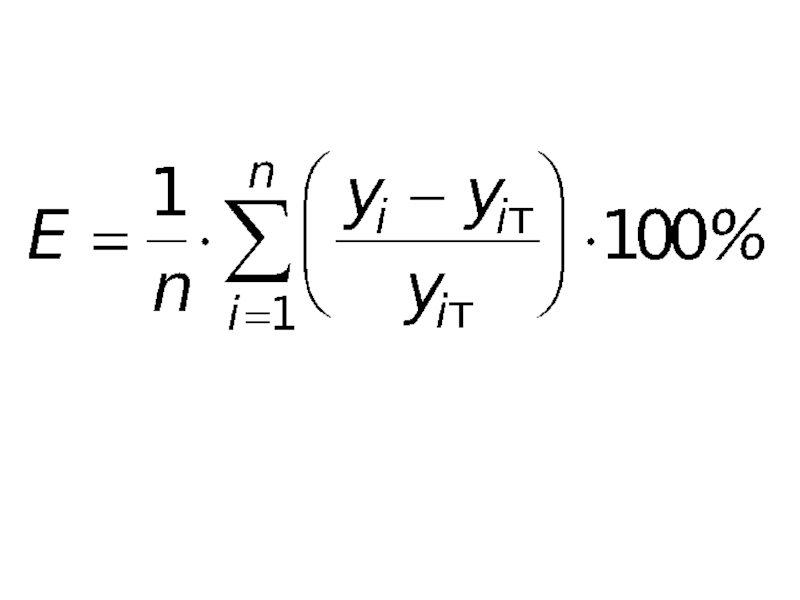- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Использование математических методов в процессе массовой оценки прогнозирования корреляционнорегрессионого анализа. (Тема 6) презентация
Содержание
- 1. Использование математических методов в процессе массовой оценки прогнозирования корреляционнорегрессионого анализа. (Тема 6)
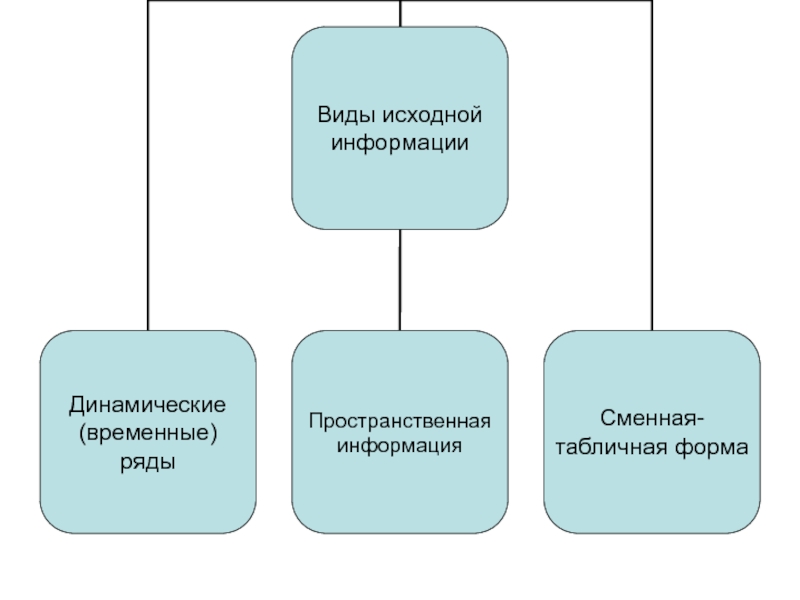
- 2. 6.1 Сущность и виды прогнозирования Основные понятия: Сущность прогнозирования Виды прогнозов
- 3. 6.2 Прогнозирование с помощью методов экстраполяции Основные
- 4. 1. Установление цели и задачи исследования, анализ
- 5. 2. Подготовка исходных данных: проверка временного ряда; формирование массива функций.
- 6. 3. Фильтрация исходного временного ряда (сглаживание и
- 7. Сглаживание по 5 точкам
- 8. Выравнивание (логарифмирование или замена переменных) где
- 9. Пример 1 Исходная функция
- 10. 4. Логический отбор видов аппроксимирующей функции а) является
- 11. Виды используемых полиномов (11) (12) (13)
- 12. (14) (15) (16) (17) (18) (19) (20)
- 14. Метод наименьших квадратов где - расчетные
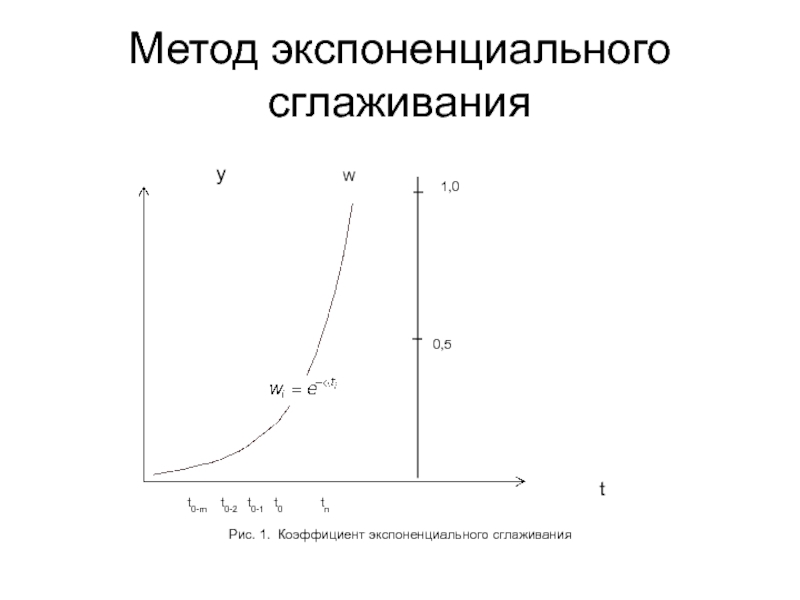
- 16. Метод экспоненциального сглаживания t0-m t0-2 t0-1 t0 tn
- 17. где - коэффициенты; -
- 18. Формула Брауна Начальные условия
- 19. Формула Брауна-Мейера где ; - оценки коэффициентов.
- 20. Линейная модель Брауна Начальные приближения для случая линейного тренда равны ; (27) (28)
- 21. ; (29) Оценки коэффициентов линейного тренда ; (31) . (32)
- 22. Прогноз на шагов (на время ) равен Ошибка прогноза
- 24. где - период прогноза;
- 25. Пример
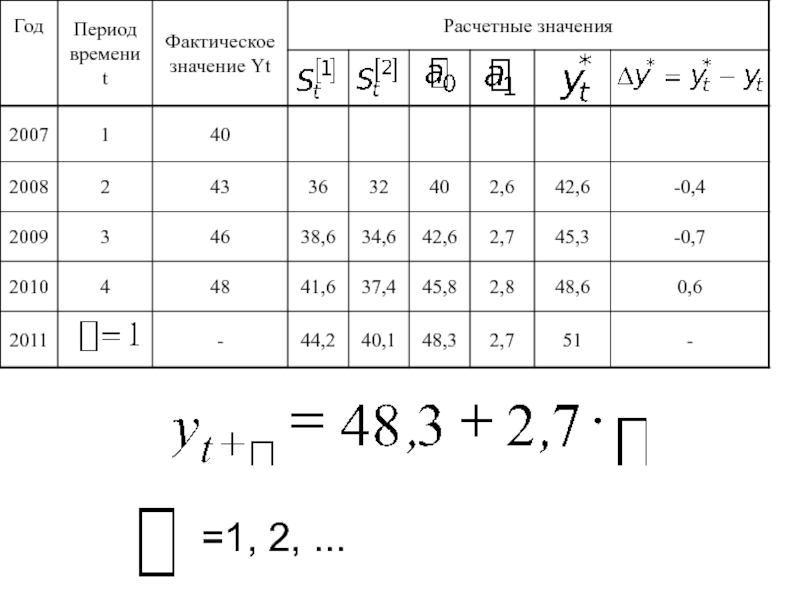
- 28. Прогноз на 2011 У = 37,5 + 2,7*5= 51
- 29. Основная ошибка
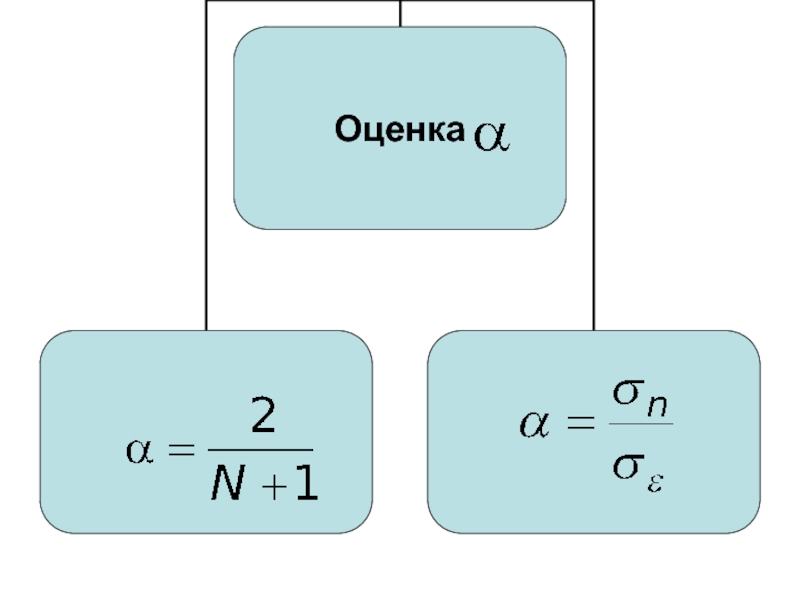
- 30. Параметр сглаживания
- 31. Для вычислим экспоненциальные средние и коэффициенты
- 33. =1, 2, ...
- 34. Ошибка прогноза
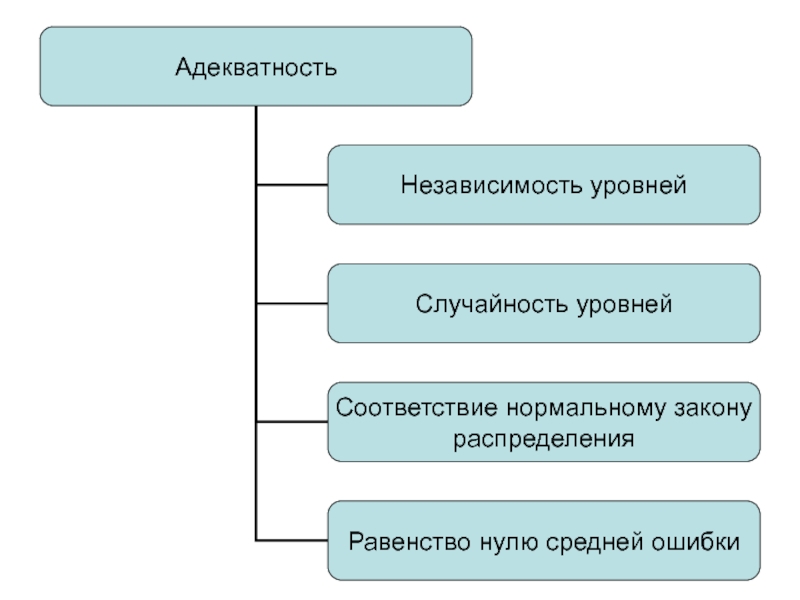
- 35. 6. Выбор математической модели прогнозирования
- 37. Независимость уровней. Критерий Дарбина-Уотсона
- 39. где - статистика Дарбина-Уотсона.
- 40. Случайность уровней
- 41. Соответствие нормальному закону распределения
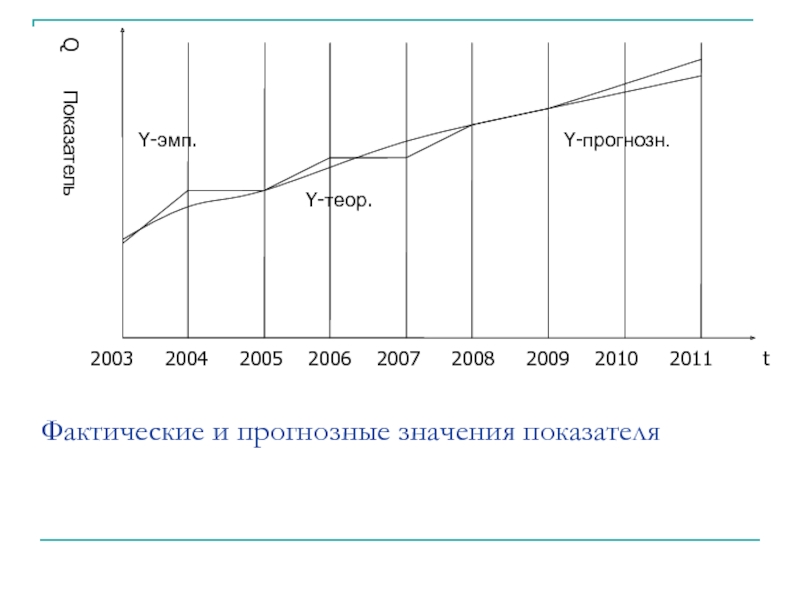
- 42. Фактические и прогнозные значения показателя
- 45. где - максимальный уровень ряда
- 46. t –критерий Стьюдента
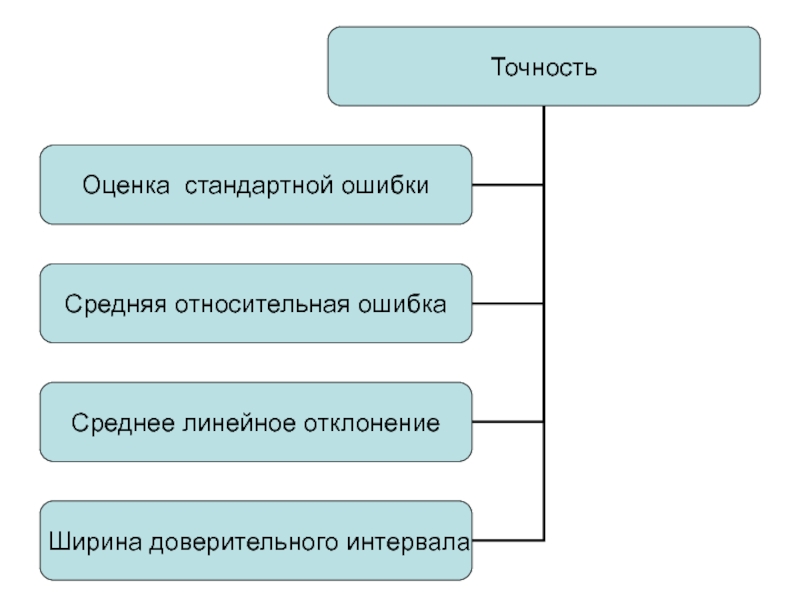
- 48. Оценка стандартной ошибки n - число
- 49. Средняя относительная ошибка оценки
- 50. Среднее линейное отклонение
- 51. Ширина доверительного интервала в точке прогноза
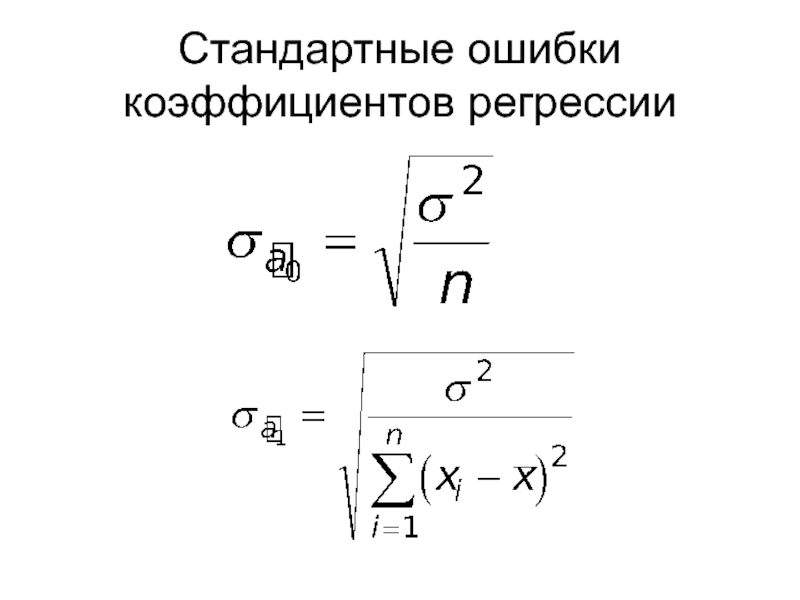
- 52. Стандартные ошибки коэффициентов регрессии
- 53. Несмещенная оценка дисперсии случайной составляющей -
- 54. - верхнее и нижнее значения
- 55. 6.3 Сущность и цели корреляционно-регрессионого анализа (КРА)
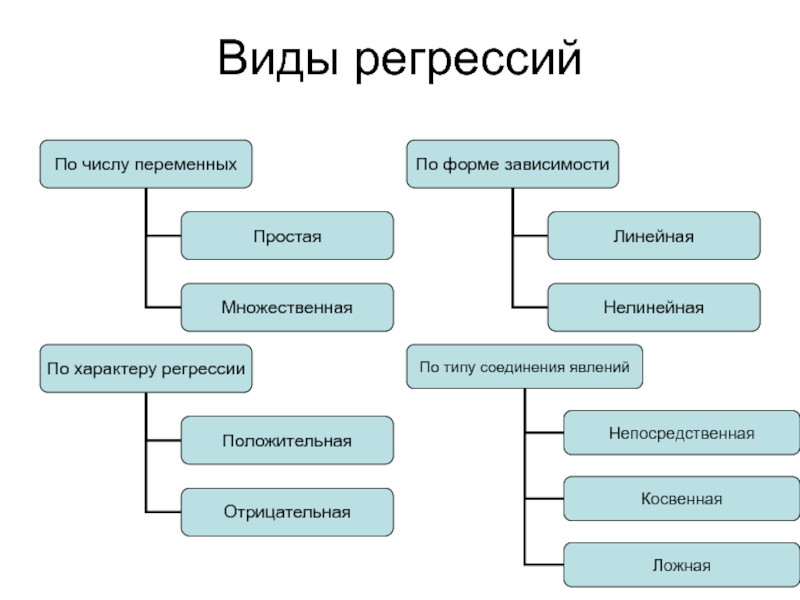
- 57. Виды регрессий
- 58. Задачи регрессионного анализа Установление формы зависимости. Определение
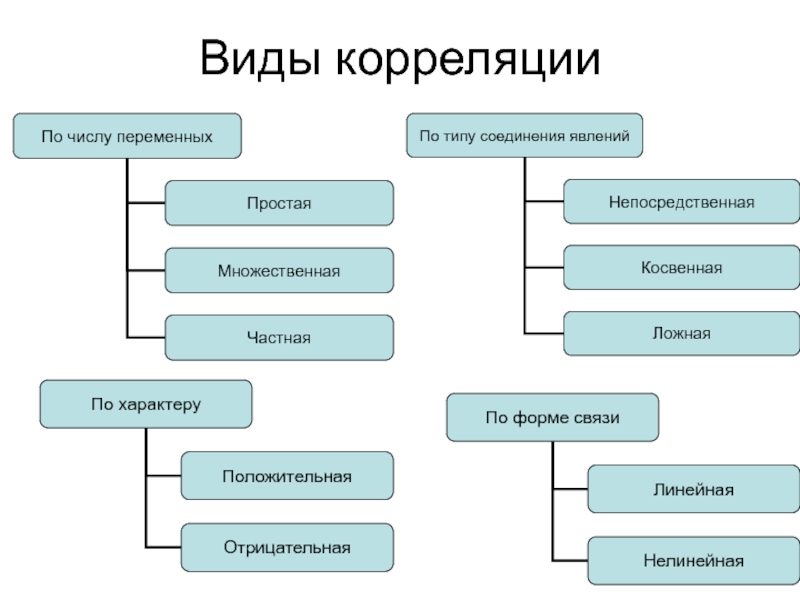
- 59. Виды корреляции
- 60. Задачи корреляционного анализа Измерение степени связности (тесноты,
- 61. Среднее значение переменной Дисперсия Основные понятия КРА
- 62. Ковариация: Коэффициент корреляции: .
- 63. Общая дисперсия Остаточная дисперсия Коэффициент множественной корреляции
- 64. Коэффициент детерминации Стандартная ошибка оценки равна
- 65. Корреляционное отношение
- 66. 6.4 Методика проведения КРА Основные понятия:
- 67. Исходные предпосылки При нахождении оценок переменной предполагается
- 68. Свойства данных оценки параметров регрессии Несмещенность Состоятельность Эффективность Достаточность
- 71. Отрицательное воздействие мультиколлинеарности: 1. Усложняется процедура выбора
- 75. =0
- 76. где - коэффициент
- 81. и
6.1 Сущность и виды прогнозирования Основные понятия: Сущность прогнозирования Виды прогнозов
Слайд 1Тема 6
Использование математических методов процессе массовой оценки
6.1 Сущность и виды прогнозирования
6.2 Прогнозирование с помощью методов экстраполяции
6.3 Сущность и цели корреляционно-регрессионого анализа (КРА)
6.4 Методика проведения КРА
Слайд 36.2 Прогнозирование с помощью методов экстраполяции
Основные понятия:
Установление цели и задачи исследования,
анализ объекта прогнозирования
Подготовка исходных данных
Фильтрация исходного временного ряда
Логический отбор видов аппроксимирующей функции
Оценка математической модели прогнозирования
Выбор математической модели прогнозирования
Подготовка исходных данных
Фильтрация исходного временного ряда
Логический отбор видов аппроксимирующей функции
Оценка математической модели прогнозирования
Выбор математической модели прогнозирования
Слайд 41. Установление цели и задачи исследования, анализ объекта прогнозирования
Анализ зависимости рассматриваемого
объекта (параметра, показателя) от других систем одного уровня и субсистемы (системы более высшего уровня);
взаимосвязи между данным объектом и другими объектами системы;
установления характера предоставления статистических данных об объекте.
взаимосвязи между данным объектом и другими объектами системы;
установления характера предоставления статистических данных об объекте.
Слайд 63. Фильтрация исходного временного ряда (сглаживание и выравнивание)
где
- значения исходной и сглаженной функции в средней точке группы;
- значение исходной и сглаженной функции в левой точке группы;
- значения исходной и сглаженной функции в правой точке группы.
- значение исходной и сглаженной функции в левой точке группы;
- значения исходной и сглаженной функции в правой точке группы.
(1)
(3)
(2)
Слайд 104. Логический отбор видов аппроксимирующей функции
а) является ли исследуемый показатель величиной монотонно
возрастающей (убывающей), стабильной, периодической, имеющей один или несколько экстремумов;
б) ограничен ли показатель сверху или снизу каким-либо пределом;
в) имеет ли функция, определяющая процесс, точку перегиба;
г) обладает ли анализируемая функция свойством симметричности;
д) имеет ли процесс четкое ограничение развития во времени.
б) ограничен ли показатель сверху или снизу каким-либо пределом;
в) имеет ли функция, определяющая процесс, точку перегиба;
г) обладает ли анализируемая функция свойством симметричности;
д) имеет ли процесс четкое ограничение развития во времени.
Слайд 14Метод наименьших квадратов
где - расчетные (теоретические) значения исходного ряда;
-
фактические значения исходного ряда;
- число наблюдений
- число наблюдений
Слайд 24
где
- период прогноза;
- среднеквадратическая ошибка аппроксимации исходного
динамического ряда.
Слайд 37Независимость уровней.
Критерий Дарбина-Уотсона
- объем выборки.
уровни фактического динамического ряда
теоретические (прогнозные) уровни динамического ряда
Слайд 45
где
- максимальный уровень ряда остатков (
),
- минимальный уровень
ряда остатков (
),
- среднеквадратическое отклонение остатков.
Слайд 53Несмещенная оценка дисперсии случайной составляющей
- фактические значения динамических рядов
и
;
- теоретическое значение, рассчитанное по уравнению регрессии;
- среднее значение фактора
.
Слайд 54
- верхнее и нижнее значения параметра
модели прогноза;
-
верхнее и нижнее значение параметра
- модели прогноза;
- значение фактора времени в точке прогноза.
Верхняя
и нижняя
границы доверительного интервала в точке прогноза
Слайд 556.3 Сущность и цели корреляционно-регрессионого анализа (КРА)
Основные понятия:
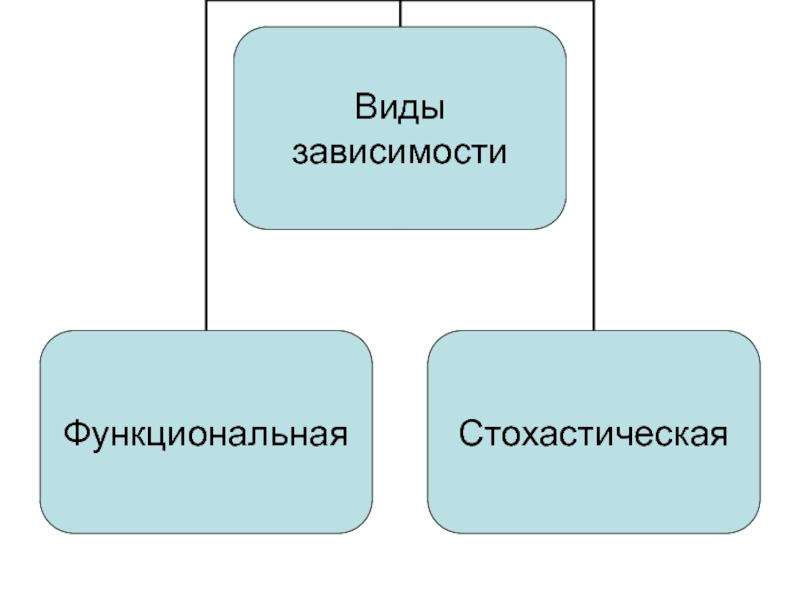
Зависимости
Регрессия
Корреляция
Задачи анализа
Уравнение регрессии
Дисперсия
Ковариация
Слайд 58Задачи регрессионного анализа
Установление формы зависимости.
Определение функции регрессии и установление влияния факторов
на зависимую переменную.
Оценка неизвестных значений переменой (экстраполяция и интерполяция).
Оценка неизвестных значений переменой (экстраполяция и интерполяция).
Слайд 60Задачи корреляционного анализа
Измерение степени связности (тесноты, силы).
Отбор факторов, оказывающих существенное влияние.
Обнаружение
неизвестных причинных связей.
Слайд 666.4 Методика проведения КРА
Основные понятия:
Исходные предпосылки
Свойства исходных данных
1. Априорное исследование экономической
проблемы.
2. Формирование перечня факторов и их логический анализ.
3. Сбор исходных данных и их первичная обработка.
4. Спецификация функции регрессии.
5. Оценка функции регрессии.
6. Отбор главных факторов.
7. Проверка адекватности модели.
8. Экономическая интерпретация.
9. Прогнозирование неизвестных значений зависимой переменной
2. Формирование перечня факторов и их логический анализ.
3. Сбор исходных данных и их первичная обработка.
4. Спецификация функции регрессии.
5. Оценка функции регрессии.
6. Отбор главных факторов.
7. Проверка адекватности модели.
8. Экономическая интерпретация.
9. Прогнозирование неизвестных значений зависимой переменной
Слайд 67Исходные предпосылки
При нахождении оценок переменной предполагается существование зависимости переменной только от
тех объясняющих переменных, которые вошли в модель (регрессию).
влияние неучтенных факторов постоянно
Отсутствует автокорреляция между возмущающими переменными
Число наблюдений должно превышать число параметров регрессии
Предполагается односторонняя зависимость переменной от факторов
Зависимая переменная и факторы распределены нормально
влияние неучтенных факторов постоянно
Отсутствует автокорреляция между возмущающими переменными
Число наблюдений должно превышать число параметров регрессии
Предполагается односторонняя зависимость переменной от факторов
Зависимая переменная и факторы распределены нормально
Слайд 68Свойства данных оценки параметров регрессии
Несмещенность
Состоятельность
Эффективность
Достаточность
Слайд 71
Отрицательное воздействие мультиколлинеарности:
1. Усложняется процедура выбора главных факторов.
2. Искажается смысл коэффициента множественной корреляции
(он предполагает независимость факторов).
3. Усложняются вычисления при построении самой модели.
4. Снижается точность оценки параметров регрессии, искажается оценка дисперсии.
3. Усложняются вычисления при построении самой модели.
4. Снижается точность оценки параметров регрессии, искажается оценка дисперсии.
Слайд 76
где
- коэффициент
-го фактора;
- среднеквадратическое отклонение к- го
фактора;
- среднеквадратическое отклонение функции
- коэффициент регрессии при К-ом факторе
