- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Интегральное исчисление функций одной переменной презентация
Содержание
- 1. Интегральное исчисление функций одной переменной
- 2. Интегральное исчисление функции одной переменной
- 3. Первообразная Определение Функция y=F(x) называется первообразной
- 4. Первообразная Теорема Если F(x) -
- 6. Свойства неопределенного интеграла Производная неопределенного
- 7. Таблица основных интегралов
- 8. Примеры табличного интегрирования 1. 2.
- 9. Примеры табличного интегрирования 3. 4. 5.
- 10. Пусть функция
- 11. Пример
- 12. Если
- 13. Метод подведения под дифференциал
- 14. Пусть функции u=u(x); v=v(x)
- 15. Типы интегралов, удобно вычисляемых методом
- 16. Примеры пример 1 пример 2
- 17. Интегрирование рациональных функций
- 18. Пример - неправильная дробь
- 19. Интегрирование рациональных функций Всякая
- 20. Интегрирование тригонометрических функций
- 21. Пример
- 22. Интегрирование тригонометрических функций
- 23. Интегрирование тригонометрических функций Пример:
- 24. Интегрирование тригонометрических функций
- 25. Интегрирование тригонометрических функций
- 26. Определенный интеграл
- 27. Определенный интеграл 4. Составим
- 29. Определенный интеграл Функция y=f(x),
- 30. Свойства определенного интеграла, вытекающие из определения
- 31. Геометрический смысл определенного интеграла
- 32. Геометрический смысл определенного интеграла
- 33. Геометрический смысл определенного интеграла
- 34. Если функция y=f(x) непрерывна
- 35. Пример
- 36. Основные свойства определенного интеграла Если
- 37. Основные свойства определенного интеграла
- 38. Основные свойства определенного интеграла Если
- 39. Основные свойства определенного интеграла Неравенство
- 40. Основные свойства определенного интеграла Если
- 41. Основные свойства определенного интеграла Производная
- 42. Если: 1) функция
- 43. Пример
- 44. Если функции u=u(x); v=v(x)
- 45. Пример
- 46. Вычисление площади фигуры
- 47. Вычисление площади фигуры 1.
- 48. Вычисление площади фигуры 2.
- 49. Вычисление площади фигуры 3.
- 50. Сводится к случаем 1, 2, 3 путем
- 51. Пример
- 52. Вычисление объема тела
- 53. Вычисление объема тела вращения Доказательство: Разобьем отрезок [a,b] точками x0=a
- 54. Вычисление объема тела вращения
- 55. Вычисление объема тела
- 56. Пример
- 57. Несобственные интегралы
- 58. Пусть функция y=f(x) непрерывна
- 59. Несобственные интегралы первого рода
- 60. Несобственные интегралы первого рода
- 61. Примеры
- 62. Пусть функция y=f(x) непрерывна
- 63. Несобственные интегралы первого рода
- 64. Несобственные интегралы второго рода
- 65. Пример
Слайд 1
Интегральное исчисление функции одной переменной
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Первообразная. Неопределенный интеграл и его свойства.
Интегрирование методом замены переменной / подведением под дифференциал. Метод интегрирования по частям.
Интегрирование рациональных / тригонометрических функций, некоторых иррациональностей.
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Определенный интеграл и его свойства. Геометрический смысл определенного интеграла.
Слайд 2
Интегральное исчисление функции одной переменной
Формула Ньютона-Лейбница.
Метод замены переменной. Метод
Приложение определенных интегралов: вычисление площадей фигур, длин дуг, объемов тел вращения.
НЕСОБСТВЕННЫЙ ИНТЕГРАЛ
Слайд 3
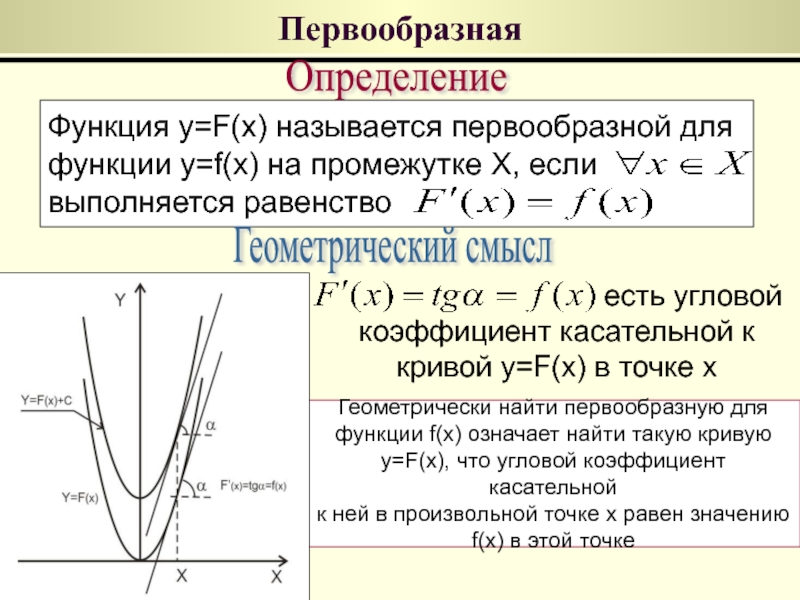
Первообразная
Определение
Функция y=F(x) называется первообразной для
функции y=f(x) на промежутке X, если
выполняется равенство
Геометрический смысл
есть угловой
коэффициент касательной к кривой y=F(x) в точке x
Геометрически найти первообразную для
функции f(x) означает найти такую кривую
y=F(x), что угловой коэффициент касательной
к ней в произвольной точке x равен значению
f(x) в этой точке
Слайд 4
Первообразная
Теорема
Если F(x) - первообразная для функции y=f(x)
на промежутке X, то все
функции у=f(x) имеют вид F(x)+c, где с –
- произвольная постоянная
(об общем виде первообразной)
Слайд 5
подынтегральная функция
подынтегральное выражение
Неопределенный интеграл
Определение
Совокупность всех первообразных для функции f(x)
на промежутке Х называется интеграл от функции f(x)
и обозначается
некоторая первообразная для функции f(x)
произвольная постоянная
Слайд 6
Свойства неопределенного интеграла
Производная неопределенного интеграла равна
подынтегральной функции
1.
Дифференциал неопределенного интеграла равен
подынтегральному выражению
2.
3.
Постоянный
интеграла
4.
5.
Это свойство справедливо для любого конечного
числа слагаемых
Слайд 10
Пусть функция
дифференцируема на промежутке T и X – множество
ее значений, на котором определена функция f(x).
Тогда (1)
Теорема
Интегрирование методом замены переменной
Слайд 12
Если
Теорема
Интегрирование методом замены переменной
(о линейной замене переменной)
Пример
Слайд 13
Метод подведения под дифференциал
Формулой замены переменной (1) можно
пользоваться и справа налево,
Этот метод называется методом подведения
под дифференциал
Пример:
Слайд 14
Пусть функции u=u(x); v=v(x) дифференцируемые
функции на промежутке X. Тогда на промежутке
выполняется формула интегрирования по частям
(2)
Теорема
Метод интегрирования по частям
Слайд 15
Типы интегралов, удобно вычисляемых методом интегрирования по частям
P(x) – многочлен, k
Удобно положить в качестве u=P(x), а за dv обозначить
все остальные сомножители
Удобно положить в качестве P(x)dx= dv, а за u
обозначить все остальные сомножители
a, b - числа
, dv - все остальные сомножители. Применить
дважды операцию интегрирования по частям.
Слайд 17
Интегрирование рациональных функций
- рациональная функция, где
- многочлен степени n
- многочлен
Если дробь неправильная, то можно выполнить
деление с остатком и представить R(x) в виде суммы некоторого многочлена и правильной дроби
Слайд 19
Интегрирование рациональных функций
Всякая правильная дробь
представлена в виде суммы простейших
дробей вида:
где A,B,C,D,M,N – некоторые действительные
числа;
a – число, при котором Q(x)=0;
p,q – числа, при которых
Теорема
Слайд 20
Интегрирование тригонометрических функций
- рациональная функция
Универсальная тригонометрическая подстановка
Замена сводит подынтегральную функцию к
Слайд 22
Интегрирование тригонометрических функций
Интегралы вида
Интегралы вида
где также вычисляются подстановкой или
ПОДСТАНОВКА
Слайд 24
Интегрирование тригонометрических функций
а) Если или
Если и целые положительные чётные числа, то используются формулы понижения порядка
Слайд 25
Интегрирование тригонометрических функций
Интегралы такого вида вычисляются путём преобразования произведений в сумму
Слайд 26
Определенный интеграл
Пусть функция y =f(x) определена на отрезке
[a,b], где a
Разобьем отрезок [a,b] точками x0=a
произвольную точку и вычислим значение функции
f(ci) в этой точке
3. Обозначим и вычислим произведение
Слайд 27
Определенный интеграл
4. Составим сумму Sn всех таких произведений, то есть
Сумма Sn вида (1) называется интегральной суммой
функции y=f(x) на отрезке [a,b]
Обозначим через - максимальную длину
отрезка разбиения.
5. Найдем предел интегральной суммы Sn при так,
что
Слайд 28 знак интеграла
подынтегральное выражение
нижний и верхний предел интегрирования
область интегрирования
Определенный интеграл
Определение
Если предел интегральной суммы Sn при так,
что существует, конечен и не зависит от способа
разбиения отрезка [a,b] и способа выбора точек c1, c2,
… cn,то этот предел называется определенным
интегралом от функции y=f(x) на отрезке [a,b] и
обозначается
Слайд 29
Определенный интеграл
Функция y=f(x), для которой существует предел
вида (2) называется интегрируемой
(2)
Слайд 30
Свойства определенного интеграла, вытекающие из определения
Определенный интеграл не зависит от
обозначения переменной
1.
Определенный интеграл с одинаковыми
пределами интегрирования равен нулю, т.е.
2.
Для
3.
Слайд 31
Геометрический смысл определенного интеграла
y=f(x) - непрерывная неотрицательная функция,
заданная
Слайд 32
Геометрический смысл определенного интеграла
Фигура, ограниченная сверху графиком функции y =f(x),
снизу
криволинейной трапецией.
Найдем площадь этой трапеции:
Разобьем отрезок [a,b] точками x0=a
произвольную точку и вычислим значение функции
f(ci) для всех
3. Обозначим и рассмотрим - площадь
прямоугольника с высотой и длиной основания , где
4. Сумма произведений площадей таких прямоугольников
равна площади ступенчатой фигуры и приближенно равна
площади криволинейной трапеции
Слайд 33
Геометрический смысл определенного интеграла
Обозначим через
отрезка разбиения.
5. С уменьшением точность приближения криволинейной
трапеции ступенчатой фигурой увеличивается, то есть
при так, что
- площадь криволинейной трапеции
Определенный интеграл от неотрицательной
непрерывной функции численно равен площади
криволинейной трапеции.
Слайд 34
Если функция y=f(x) непрерывна на отрезке [a,b] и F(x) –
какая-либо ее
место формула Ньютона-Лейбница
Формула Ньютона-Лейбница
Теорема
Слайд 36
Основные свойства определенного интеграла
Если с – постоянное число и функция f(x)
интегрируема на отрезке [a,b], то
Свойство 1
Если функции f1(x) и f2(x) интегрируемы на отрезке
[a,b], то интегрируема на этом отрезке их сумма
Свойство 2
Это свойство распространяется на сумму любого конечного числа слагаемых
Слайд 37
Основные свойства определенного интеграла
Свойство 3
Если функция f(x) интегрируема на отрезке [a,b]
и
Свойство 4
Слайд 38
Основные свойства определенного интеграла
Если функция f(x) непрерывна на отрезке [a,b]
, то
Свойство 5
(теорема о среднем)
Если функция f(x) сохраняет знак на отрезке [a,b], Свойство 6
где a
функция f(x), то есть если для
, то
Слайд 39
Основные свойства определенного интеграла
Неравенство между непрерывными на отрезке [a,b]
функциями можно интегрировать
Если
Свойство 7
Слайд 40
Основные свойства определенного интеграла
Если m и M соответствующее наименьшее и
наибольшее
(a
Свойство 8
(Оценка интеграла)
Слайд 41
Основные свойства определенного интеграла
Производная определенного интеграла с
переменным верхнем пределом по
равна подынтегральной функции для этого предела,
то есть
Свойство 9
Слайд 42
Если: 1) функция
непрерывны при
2) множеством значений функции при
является отрезок [a,b]
3)
Тогда (1)
Теорема
Интегрирование методом замены переменной
Замечание:
При вычислении определенного интеграла
методом замены переменной возвращаться к
старой переменной не надо.
2.Необходимо менять пределы интегрирования
при замене переменной.
Слайд 44
Если функции u=u(x); v=v(x) имеют непрерывные
производные на отрезке [a,b], то справедлива
формула
(5)
Теорема
Метод интегрирования по частям
Слайд 46
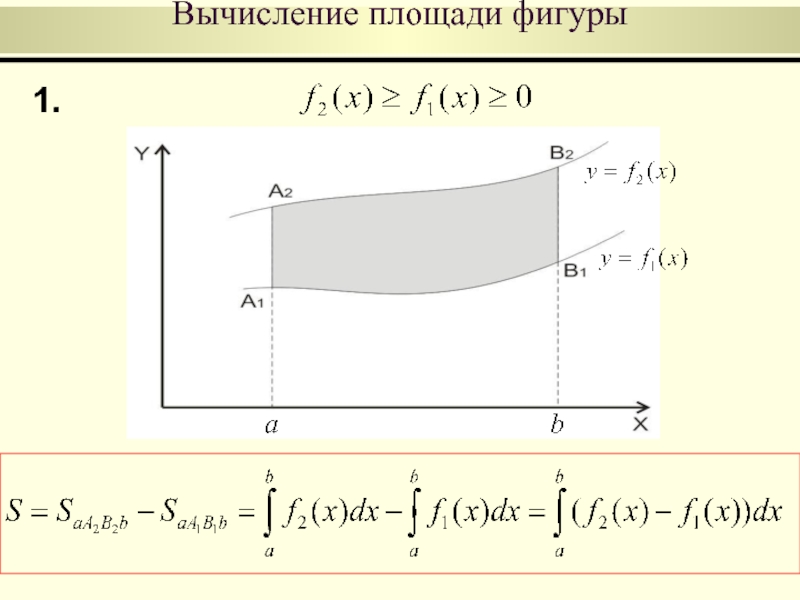
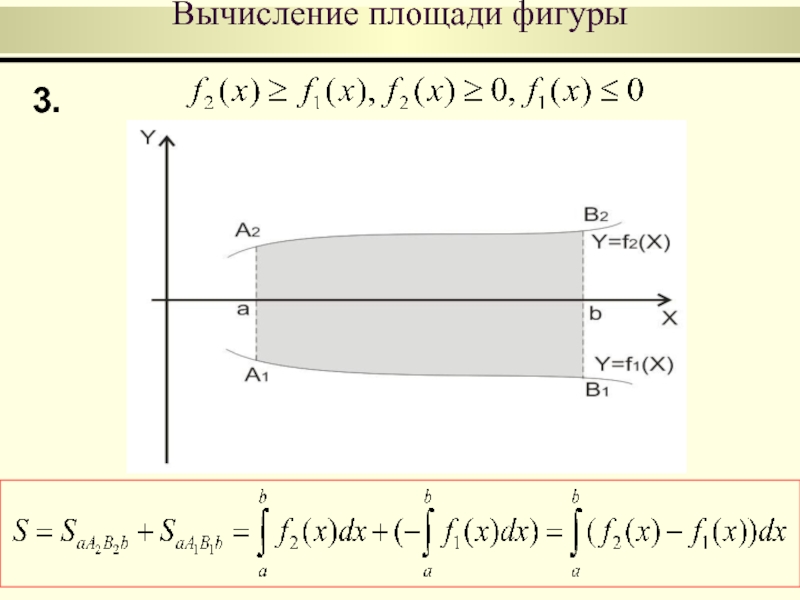
Вычисление площади фигуры
Пусть на отрезке [a,b] заданы непрерывные функции
Тогда площадь фигуры, заключенной между кривыми
и на отрезке [a,b] вычисляется по формуле
Слайд 50Сводится к случаем 1, 2, 3 путем разбиения отрезка
[a,b] на
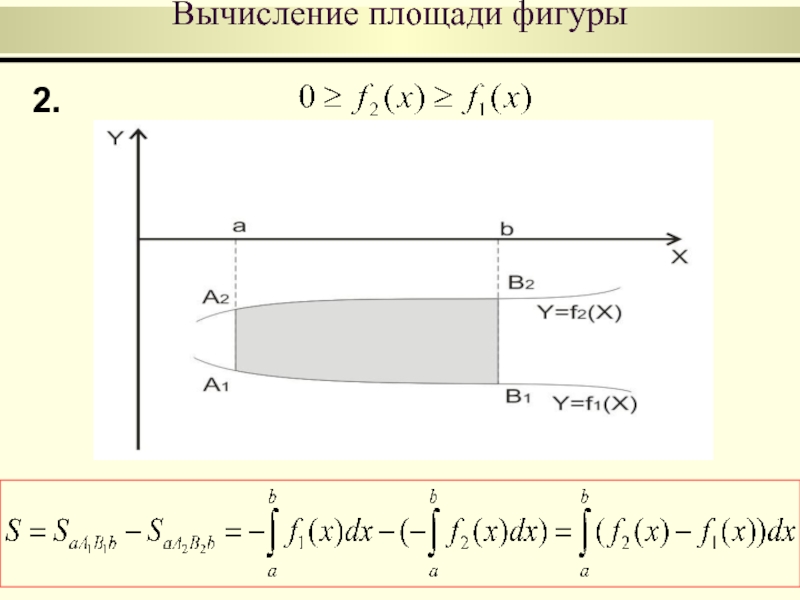
Вычисление площади фигуры
4.
Слайд 52
Вычисление объема тела вращения
Пусть функция y=f(x) непрерывна и неотрицательна
на отрезке
Тогда тело, которое образуется при вращении вокруг
оси OX криволинейной трапеции aABb, имеет объем:
Слайд 53
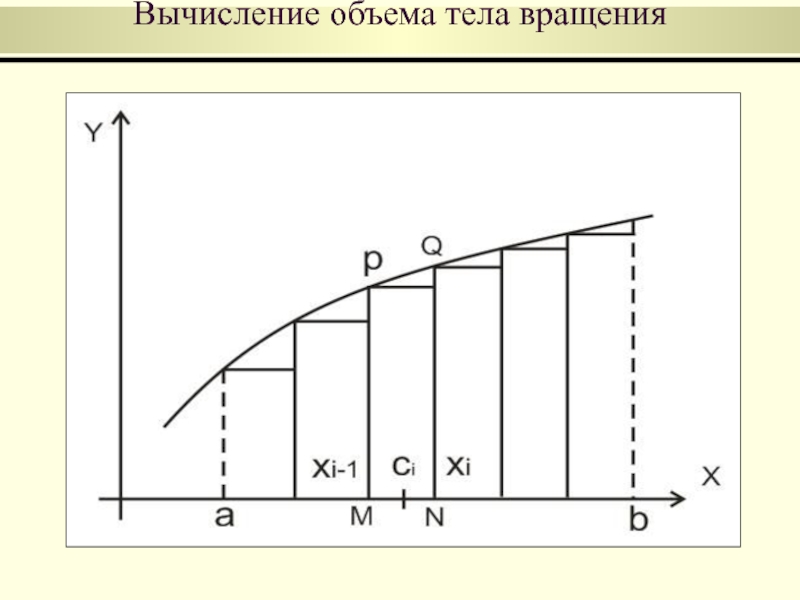
Вычисление объема тела вращения
Доказательство:
Разобьем отрезок [a,b] точками x0=a
2. На каждом частичном отрезке [xi-1, xi] построим
прямоугольник MPQN. Выберем произвольную точку
3. При вращении вокруг оси ОХ прямоугольник MPQN опишет
цилиндр, объем которого будет равен , где
- высота цилиндра, - радиус основания
4. Сумма является приближением для искомого
объема
Слайд 55
Вычисление объема тела вращения
Пусть функция y=f(x) непрерывна и неотрицательна
на отрезке
Тогда тело, которое образуется при вращении вокруг
оси OY криволинейной трапеции, имеет объем:
Слайд 57
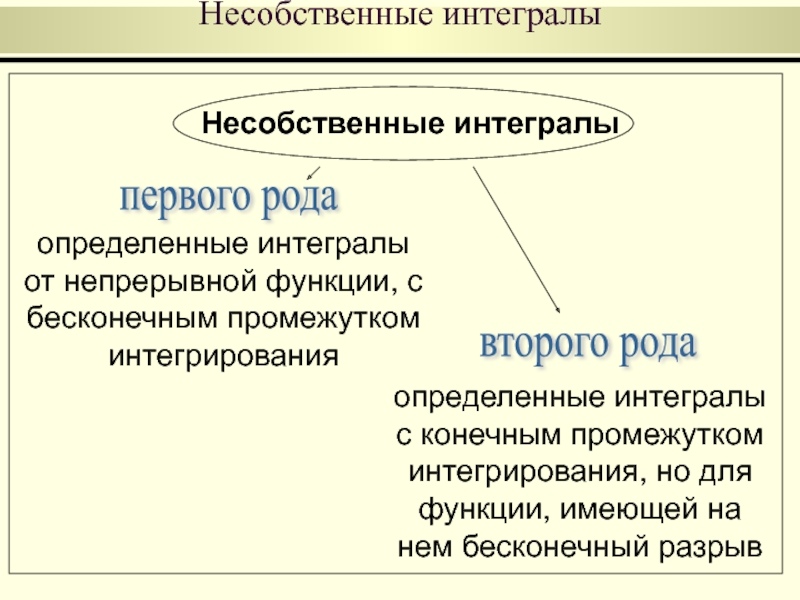
Несобственные интегралы
Несобственные интегралы
определенные интегралы от непрерывной функции, с бесконечным промежутком
определенные интегралы с конечным промежутком интегрирования, но для функции, имеющей на нем бесконечный разрыв
первого рода
второго рода
Слайд 58
Пусть функция y=f(x) непрерывна на промежутке
, то его называют несобственным
интегралом первого рода и обозначают
Определение
Несобственные интегралы первого рода
Если существует конечный предел, то говорят, что несобственный интеграл сходится, в противном случае (не существует или бесконечен) - расходится
Слайд 59
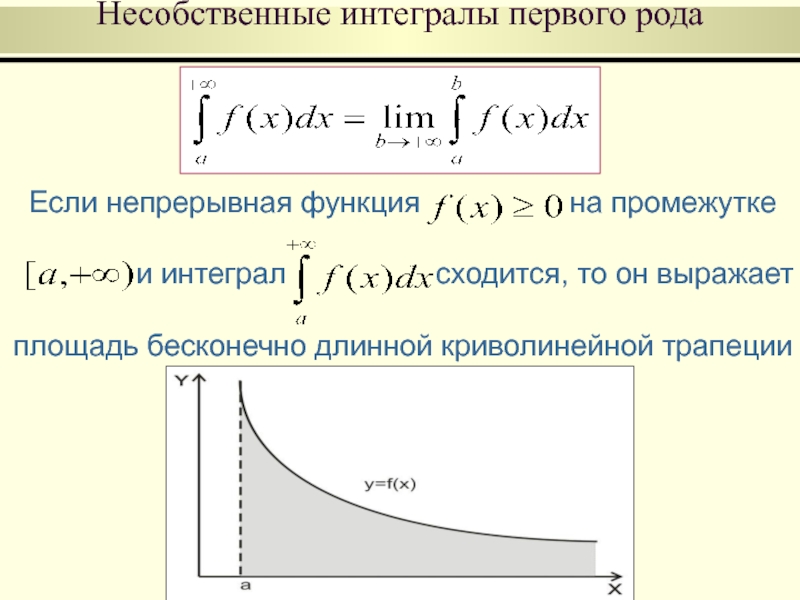
Несобственные интегралы первого рода
Если непрерывная функция
и интеграл сходится, то он выражает
площадь бесконечно длинной криволинейной трапеции
Слайд 60
Несобственные интегралы первого рода
Несобственный интеграл на промежутке
Несобственный интеграл с двумя бесконечными пределами
С – произвольное число
Слайд 62
Пусть функция y=f(x) непрерывна на промежутке
существует конечный предел вида
то его называют несобственным интегралом второго
рода и обозначают
Определение
Несобственные интегралы второго рода
Если существует конечный предел, то говорят, что несобственный интеграл сходится, в противном случае (не существует или бесконечен) - расходится
Слайд 63
Несобственные интегралы первого рода
Если функция f(x)>0 на промежутке [a,b] и интеграл
сходится, то он выражает
площадь бесконечно высокой криволинейной трапеции
























![Определенный интегралПусть функция y =f(x) определена на отрезке[a,b], где a](/img/tmb/2/181583/a665b3b877f2df1dff177de18d8eb49a-800x.jpg)


](/img/tmb/2/181583/dc27c50cb6cef49702057e0a617d5a2d-800x.jpg)

![Геометрический смысл определенного интеграла y=f(x) - непрерывная неотрицательная функция,заданная на отрезке [a,b] a](/img/tmb/2/181583/ca90ab22b9b98f9d93d02958f08b6847-800x.jpg)


![Если функция y=f(x) непрерывна на отрезке [a,b] и F(x) –какая-либо ее первообразная на отрезке [a,b],](/img/tmb/2/181583/1b699ad2a00b45684a9264c4cc0cc9da-800x.jpg)

![Основные свойства определенного интегралаЕсли с – постоянное число и функция f(x) интегрируема на отрезке [a,b],](/img/tmb/2/181583/6b3cfe1437ecc679462c1cbe5d013bcb-800x.jpg)
![Основные свойства определенного интегралаСвойство 3Если функция f(x) интегрируема на отрезке [a,b]и a](/img/tmb/2/181583/be4e10253a53ad4dc33241186707b1e8-800x.jpg)
![Основные свойства определенного интегралаЕсли функция f(x) непрерывна на отрезке [a,b], то](/img/tmb/2/181583/328f8e08c694916a0436de4b141d7534-800x.jpg)
![Основные свойства определенного интегралаНеравенство между непрерывными на отрезке [a,b]функциями можно интегрироватьЕсли](/img/tmb/2/181583/499908cfb1f010f528e226f46ae5a56f-800x.jpg)




![Если функции u=u(x); v=v(x) имеют непрерывныепроизводные на отрезке [a,b], то справедливаформула интегрирования по частям](/img/tmb/2/181583/dbe36f4143f29334ba337513b906a881-800x.jpg)

![Вычисление площади фигурыПусть на отрезке [a,b] заданы непрерывные функции и такие,](/img/tmb/2/181583/c50748a014ab3f07c5c780ecb77b1c6d-800x.jpg)
![Сводится к случаем 1, 2, 3 путем разбиения отрезка [a,b] на отдельные отрезки [a,c], [c,d],](/img/tmb/2/181583/7a3dcac4589b450dab9b5d79095055db-800x.jpg)

![Вычисление объема тела вращенияПусть функция y=f(x) непрерывна и неотрицательна на отрезке [a,b].Тогда тело, которое образуется](/img/tmb/2/181583/0548cdd968b92034196266deb5956c85-800x.jpg)
![Вычисление объема тела вращенияДоказательство:Разобьем отрезок [a,b] точками x0=a](/img/tmb/2/181583/57f2f03f9274b83beb620b35eaa11bdc-800x.jpg)
![Вычисление объема тела вращенияПусть функция y=f(x) непрерывна и неотрицательна на отрезке [a,b].Тогда тело, которое образуется](/img/tmb/2/181583/146b1e4b8ab4626c9c38468c5630209a-800x.jpg)





![Несобственные интегралы первого родаЕсли функция f(x)>0 на промежутке [a,b] и интеграл](/img/tmb/2/181583/54bf373ed9b2d89be865d71228199e01-800x.jpg)