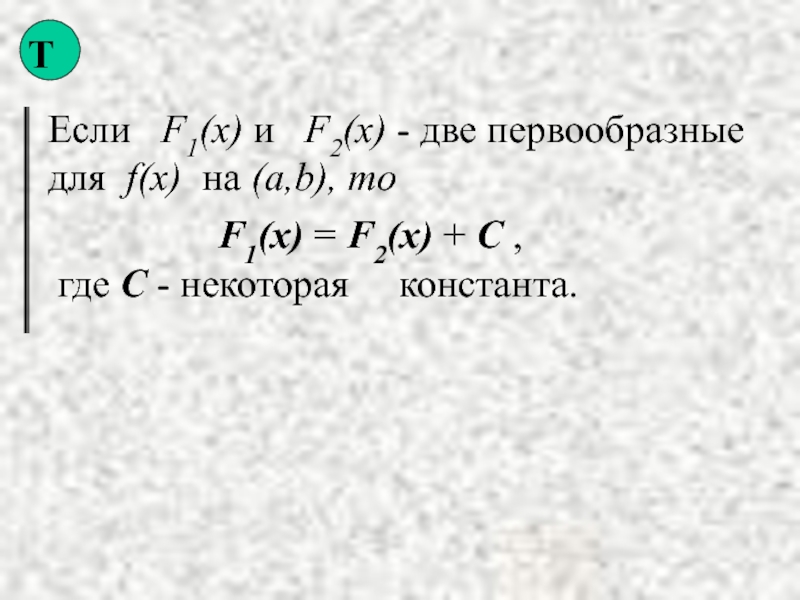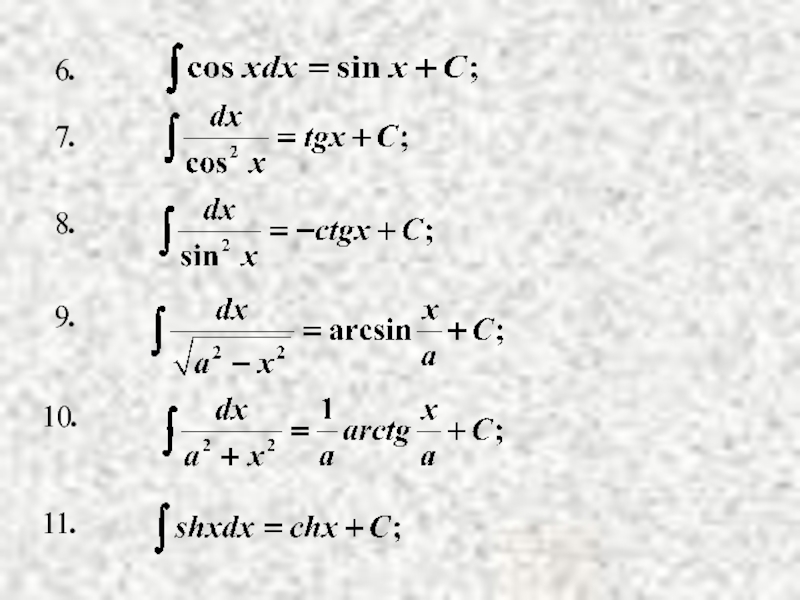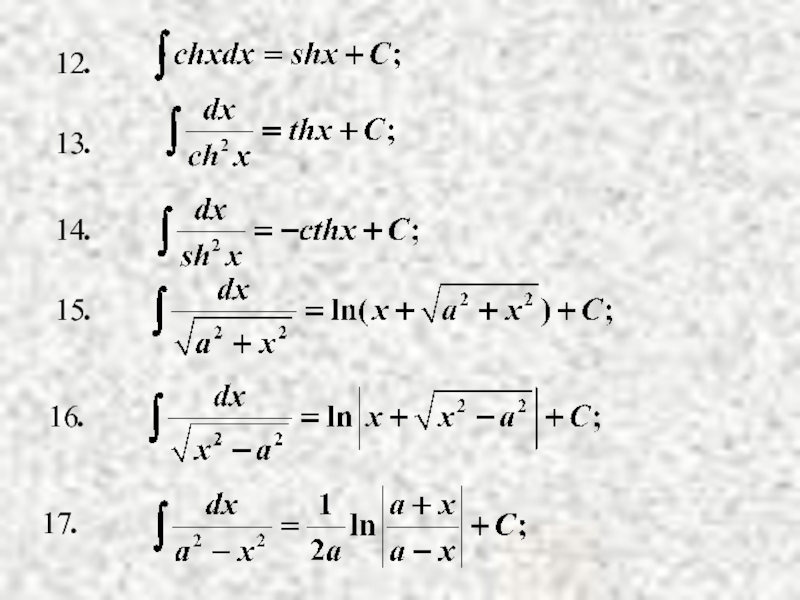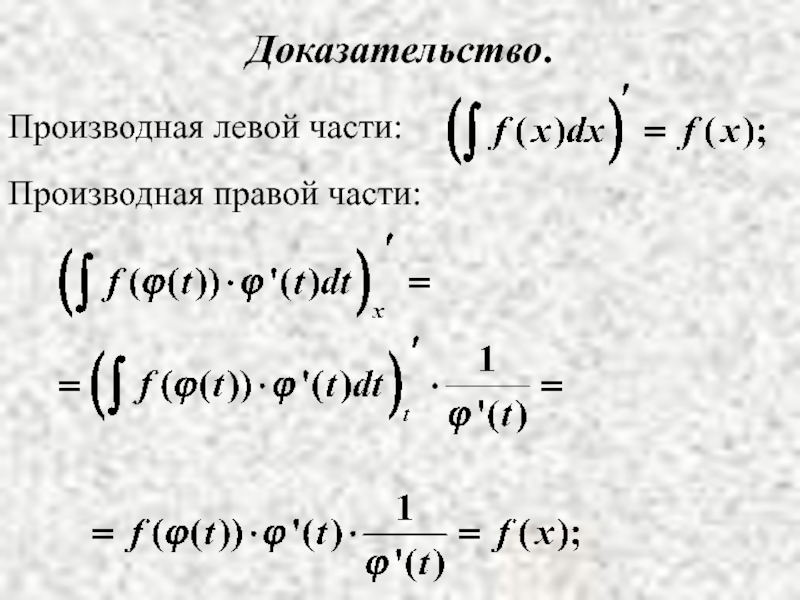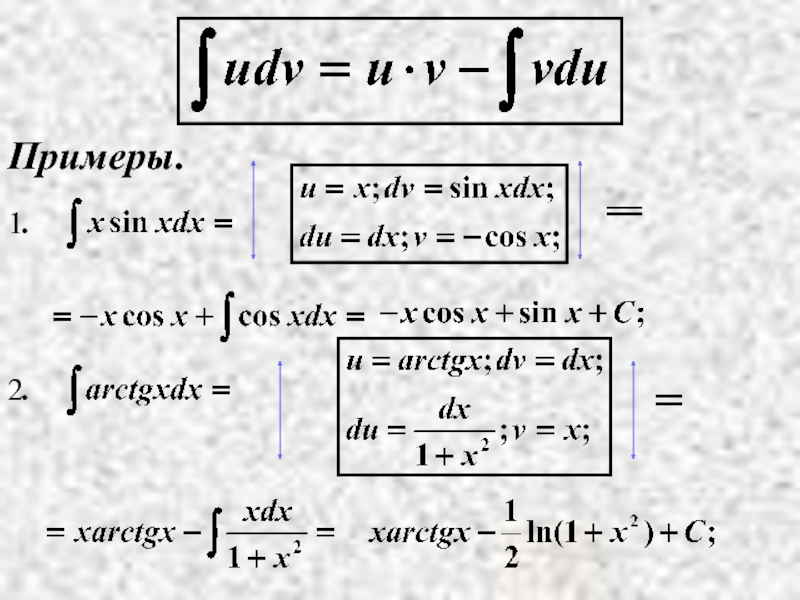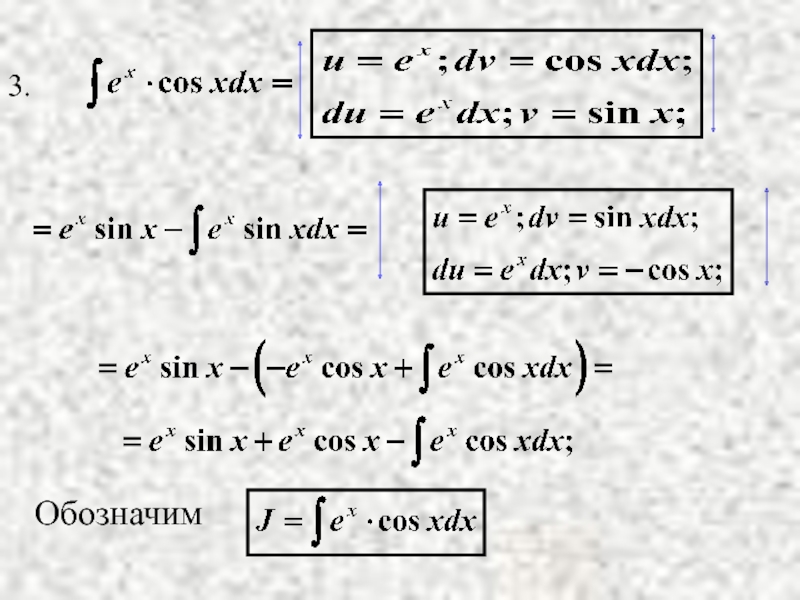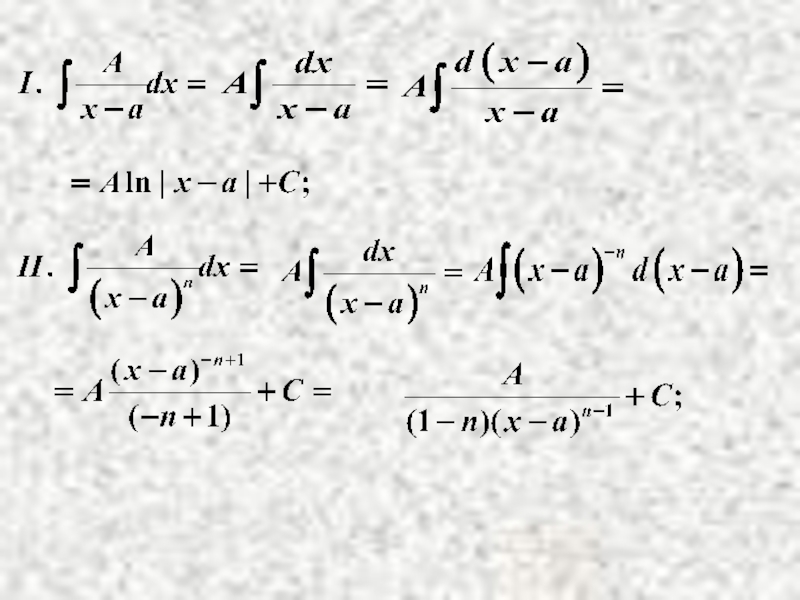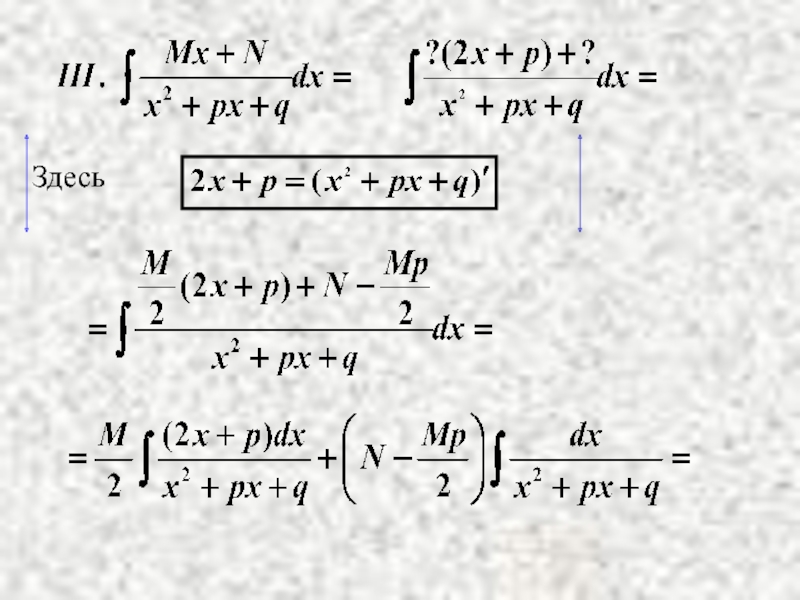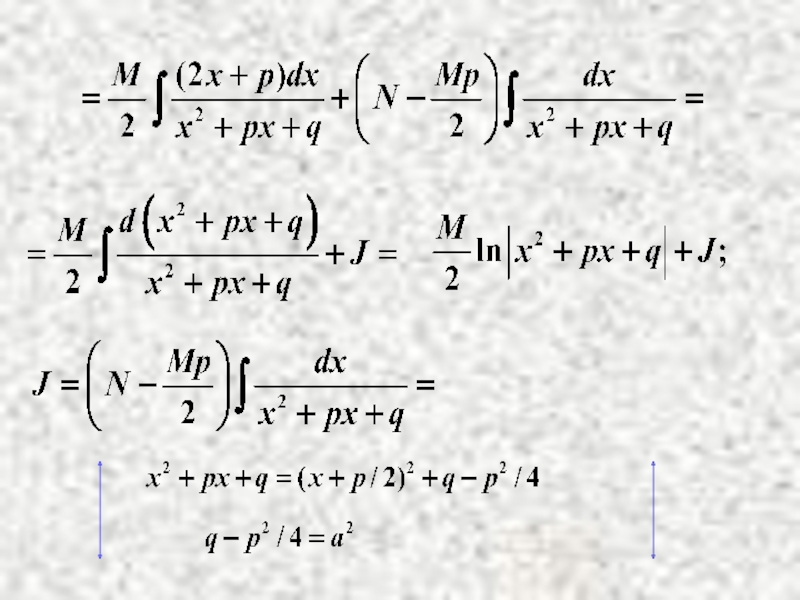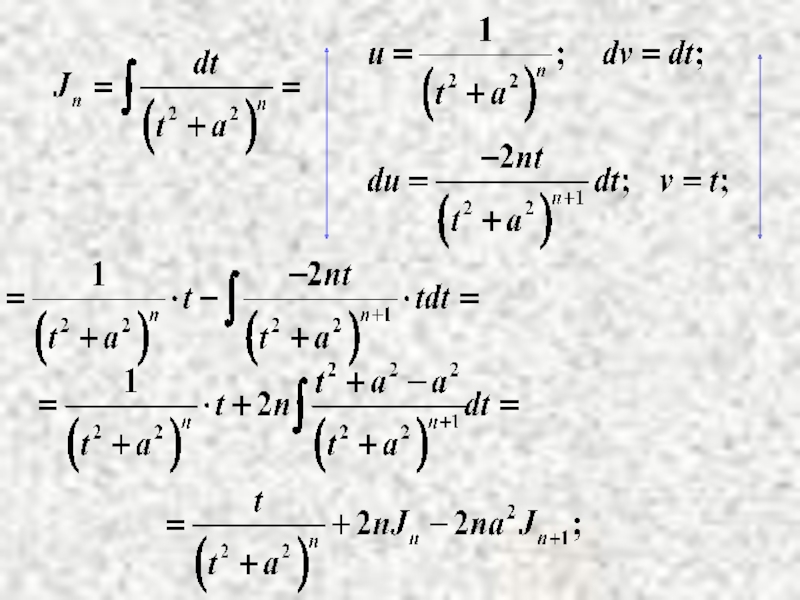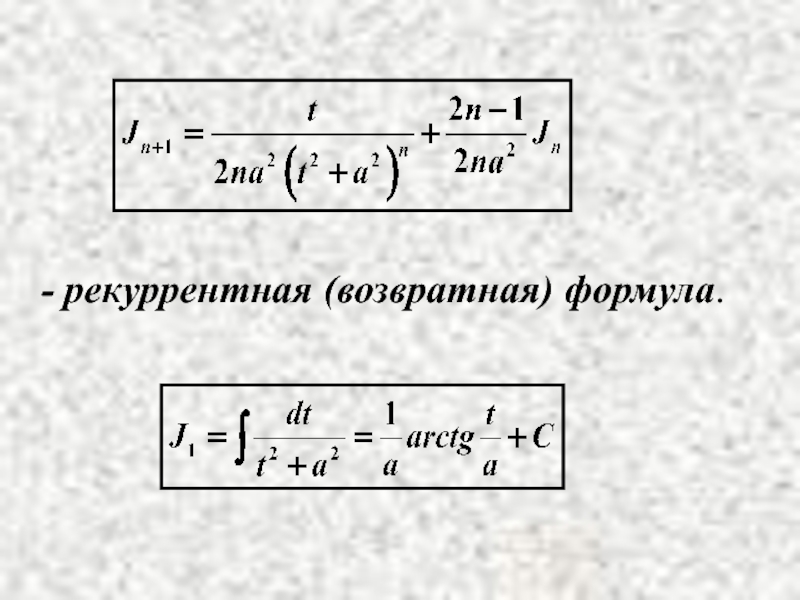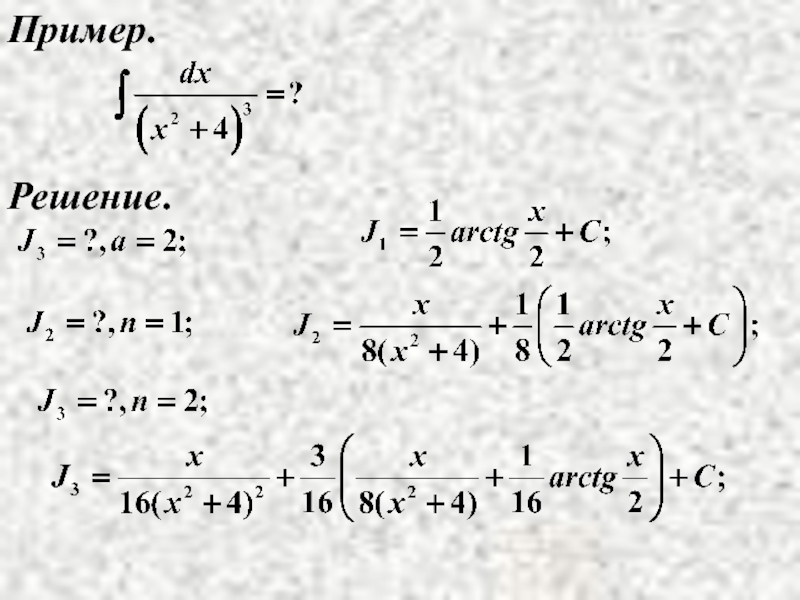- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Интегральное исчисление презентация
Содержание
- 1. Интегральное исчисление
- 2. Лекция 5 2. Методы интегрирования. 3.
- 3. Неопределенный интеграл и его свойства. Примеры. 1. 2. 3.
- 4. Если F1(x) и F2(x) -
- 5. Доказательство. Вывод. Если F(x) - первообразная для
- 6. Обозначение неопределённого интеграла:
- 7. Свойства неопределенного интеграла. 1. 2. 3. 4.
- 8. Таблица неопределенных интегралов.
- 11. I. Замена переменной в неопределенном интеграле.
- 12. Доказательство. Производная левой части: Производная правой части:
- 13. Замечание. Формулой замены переменной
- 14. II. Интегрирование по частям. Рассмотрим
- 15. Примеры.
- 18. Такие интегралы называются возвратными.
- 19. Классы интегрируемых функций. Простейшие дроби. К простейшим
- 21. Здесь
- 27. - рекуррентная (возвратная) формула.
- 28. Пример. Решение.
Лекция 5 2. Методы интегрирования. 3. Классы интегрируемых функций. 1. Неопределенный интеграл и его свойства. Интегральное исчисление
Слайд 2
Лекция 5
2. Методы интегрирования.
3. Классы интегрируемых функций.
1. Неопределенный интеграл и его
свойства.
Интегральное исчисление
Слайд 4Если F1(x) и F2(x) - две первообразные для f(x)
на (a,b), то
F1(x) = F2(x) + С ,
где С - некоторая константа.
Слайд 5Доказательство.
Вывод.
Если F(x) - первообразная для функции f(x) на интервале (a,b), то
Ф(х) = F(x)+ С - также её первообразная.
Слайд 13Замечание.
Формулой замены переменной можно пользоваться
“слева
- направо’’ и “справа - налево’’
(подведение новой переменной под знак дифференциала).
(подведение новой переменной под знак дифференциала).
Примеры.
Слайд 16
Замечание.
Формулу интегрирования по частям можно применять
несколько раз.
за u обозначается логарифм или обратная тригонометрическая функция.
Слайд 19Классы интегрируемых функций.
Простейшие дроби.
К простейшим дробям относятся:
A,M,N,a,p,q - действительные
числа, n – натуральное
число.
число.
