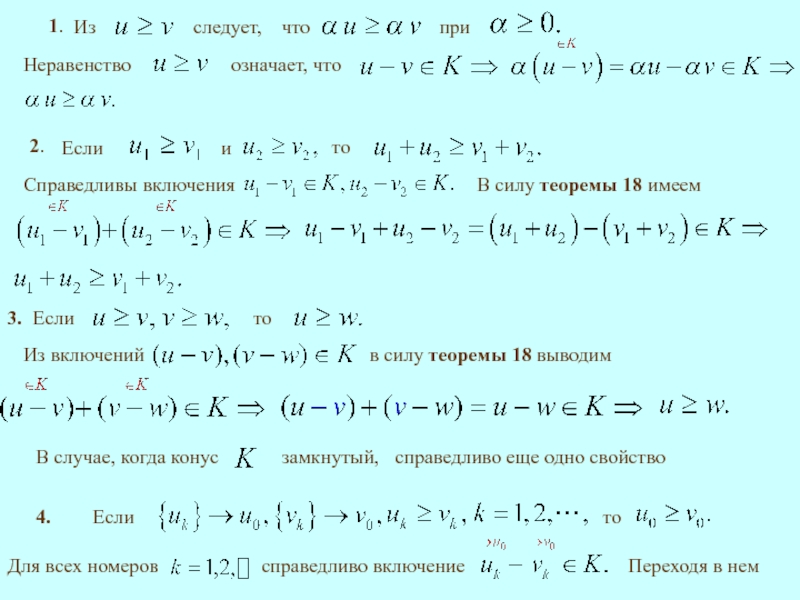- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Выпуклый анализ. Выпуклые множества. Лекция 9 презентация
Содержание
- 1. Выпуклый анализ. Выпуклые множества. Лекция 9
- 2. 2. ВЫПУКЛЫЕ МНОЖЕСТВА (ПРОДОЛЖЕНИЕ)
- 4. Пример 11. Приведем некоторые свойства выпуклых конусов. Решение.
- 5. Теорема 19. Доказательство. и
- 6. Приведем важный пример конуса. Упражнение 1.
- 8. 2.9. Выпуклые конусы и
- 10. Упражнение.
- 11. 2.10. Многокритериальная оптимизация. Рассмотрим
- 12. Упражнение 1. Решение. Пусть Тогда
- 13. Определение 15. Полагаем
- 15. Упражнение 2. Найти все точки Парето в задачи векторной оптимизации
Слайд 2
2. ВЫПУКЛЫЕ МНОЖЕСТВА (ПРОДОЛЖЕНИЕ)
2.8. Выпуклые конусы.
2.9. Выпуклые конусы и частичная
2.10. Многокритериальная оптимизация.
Слайд 3
2.8. Выпуклые конусы.
Выпуклый конус
Определение 13.
то конус называется выпуклым,
если открыто
2. ВЫПУКЛЫЕ МНОЖЕСТВА (ПРОДОЛЖЕНИЕ)
Пример 10.
Множества
являются выпуклыми конусами,
Слайд 6Приведем важный пример конуса.
Упражнение 1.
(конусная оболочка) является конусом.
Решение.
Теорема 20.
Доказательство.
Тогда
Слайд 8
2.9. Выпуклые конусы и частичная упорядоченность.
можно ввести частичный порядок его
Определение 14.
Заметим, что если
то
Перечислим и докажем ряд свойств введенного отношения,
Когда ясно, о каком конусе идет речь,
Слайд 9
то
Справедливы включения
В силу теоремы 18 имеем
Из включений
в
Если
Переходя в нем
1.
2.
4.
справедливо еще одно свойство