- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Оптимальное планирование эксперимента презентация
Содержание
- 1. Оптимальное планирование эксперимента
- 2. Литература Н.А. Спирин, В.В. Лавров. Методы планирования
- 3. Цель планирования эксперимента нахождение таких условий и
- 4. Вводные понятия Эксперимент – система операций, воздействий
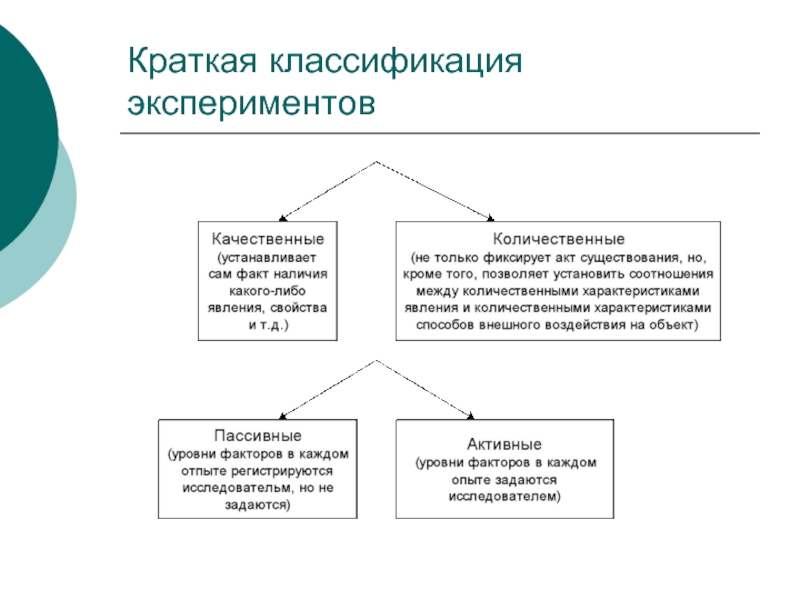
- 5. Краткая классификация экспериментов
- 6. Функция отклика -
- 7. Активный эксперимент Основная задача – определить коэффициенты
- 8. Последовательность проведения активного эксперимента Разрабатывается схема проведения
- 9. Планирование активного эксперимента При планировании экспериментов чаще
- 10. Планирование первого порядка В качестве факторов выбираются
- 11. Представления плана эксперимента (на примере эксперимента с
- 12. Свойства матрицы представления эксперимента 1. Свойство симметричности
- 13. Определение коэффициентов b уравнения регрессии По свойствам
- 14. Планирование второго порядка Применяется если описание функции
- 15. Ортогональный план Ортогональный план 2-ого порядка Это
- 16. Ротатабельный план Ротабельный план 2-ого порядка Это
Слайд 2Литература
Н.А. Спирин, В.В. Лавров. Методы планирования и обработки инженерного эксперимента: Конспект
Джонсон Н. Лион Ф. Статистика и планирование эксперимента в технике и науке: Методы планирования эксперимента. – М.: Мир, 1981. – 520 с.
Красовский Г.И., Филаретов Г.Ф. Планирование эксперимента. – Мн.: Изд-во БГУ, 1982. – 302 с.
Слайд 3Цель планирования эксперимента
нахождение таких условий и правил проведения опытов при которых
Слайд 4Вводные понятия
Эксперимент – система операций, воздействий и (или) наблюдений, направленных на
Опыт – воспроизведение исследуемого явления в определенных условиях проведения эксперимента при возможности регистрации его результатов [1]
Фактор – переменная величина, по предположению зависящая влияющая на результат эксперимента
Отклик – наблюдаемая случайная переменная, по предположению зависящая от факторов [1]
Функция отклика – зависимость мат. ожидания отклика от факторов [1]
Слайд 7Активный эксперимент
Основная задача – определить коэффициенты функции отклика
Уравнение (*),
x, x – переменные факторы при i=1,…k; u=1,…k; i!=u (k-число факторов)
коэффициенты влияния факторов
регрессионная модель (коэффициенты регрессии определяются экспериментально)
Полнофакторный эксперимент (ПФЭ) – эксперимент, реализующий все возможные неповторяющиеся комбинации уровней независимых факторов
Слайд 8Последовательность проведения активного эксперимента
Разрабатывается схема проведения исследований, т.е. выполняется планирование эксперимента
Осуществляется
Выполняется обработка результатов измерений
Слайд 9Планирование активного эксперимента
При планировании экспериментов чаще всего применяются планы 1-ого и
Планы 1-ого порядка – это планы, которые позволяют провести эксперимент для отыскания уравнения регрессии, содержащее только первые степени факторов и их произведения
Планы 2-ого порядка – это планы, которые позволяют провести эксперимент для отыскания уравнения регрессии, содержащие вторые степени факторов
Слайд 10Планирование первого порядка
В качестве факторов выбираются только контролируемые и управляемые факторы
Обеспечивается возможность независимого изменения каждого из факторов и поддержание его на определенном уровне
Для каждого фактора указывается интервал (+/-), в пределах которого ставится исследование
Слайд 11Представления плана эксперимента
(на примере эксперимента с 3-мя независимыми факторами)
Табличное (матричное) представление
Геометрическое
Уравнением регрессии
b0, b1, b2, b3 – коэффициенты регрессии
xi*xu – члены двойного взаимодействия
x1*x2*x3 – члены тройного взаимодействия
Слайд 12Свойства матрицы представления эксперимента
1. Свойство симметричности – алгебраическая сумма элементов вектор-столбца
2. Свойство нормирования – сумма квадратов каждого столбца равна числу опытов
3. Свойство ортогональности – скалярное произведение всех вектор-столбцов (сумма почленных произведений элементов любых вектор столбцов) равно нулю
i = номер фактора, j – номер опыта
Слайд 13Определение коэффициентов b уравнения регрессии
По свойствам матрицы планирования
Методом наименьших квадратов находятся
Получаем
Слайд 14Планирование второго порядка
Применяется если описание функции отклика первым порядком получается недостаточным
Каждый фактор варьируется не менее чем на трех уровнях – полный эксперимент содержит 3^k (k – количество факторов) опытов.
План 2-ого порядка при k=2 n=1
Опыты проводятся
В «крайних точках» - как в планировании 1-ого порядка
В «звездных точках» - xi=(+/-)a, xj=0, 1,…,n; 1,…,n; i!=j
В «центре» - xi=0, j=1,2,3,…,n
Уравнение регрессии для эксперимента с 2-мя факторами
Слайд 15Ортогональный план
Ортогональный план 2-ого порядка
Это план 2-ого порядка после преобразований (*)
Эти
Тогда уравнение регрессии
В итоге уравнение регрессии преобразуется к виду
Слайд 16Ротатабельный план
Ротабельный план 2-ого порядка
Это план, у которого точки плана располагаются
В таком плане точность оценивания функции отклика по любому направлению факторного пространства (для всех точек плана) одинаковая, что позволяет наилучшим образом извлечь максимальное количество (несмещенной) информации из плана
Для того, что бы привести план 2-ого порядка к рототабельному величину плеча выбирают из условия (**)




![Функция отклика- это зависимость математического ожидания отклика от факторов [1]](/img/tmb/1/22173/ca0f09989f949bed7ec0c709dbb9d67f-800x.jpg)















