- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Интегральное исчисление презентация
Содержание
- 1. Интегральное исчисление
- 2. Функция
- 3. Задача Например:
- 4. Совокупность всех первообразных для функции
- 5. Свойства неопределённого интеграла Производная неопределённого интеграла равна
- 6. Свойства неопределённого интеграла Постоянный множитель можно выносить
- 7. Свойства неопределённого интеграла Об инвариантности формул интегрирования.
- 8. Задача Например:
- 9. Основные формулы интегрирования
- 10. Основные формулы интегрирования
- 11. Основные формулы интегрирования
- 12. Интегрирование Рассмотрим некоторые из основных
- 13. Задача Пример. Найти
- 14. Задача Решение:
- 15. Задача Пример. Найти
- 16. Задача Пример. Найти Решение:
- 17. Задача Пример. Найти
- 18. Задача Пример. Найти Решение:
- 19. Задача 2. Метод замены переменной.
- 20. Задача Решение.
- 21. Задача Пример. Найти
- 22. Задача Пример. Найти Решение:
- 23. Задача Можно использовать вместо замены переменной
- 24. Задача Некоторые другие примеры внесения под знак дифференциала:
- 25. Задача Получение линейной функции:
- 26. Задача Пример: Найти
- 27. Задача Решение:
- 28. Задача Решение 1-го примера из этого типа:
- 29. Задача Пример. Найти
- 30. Задача Решение:
- 31. Задача Пример. Найти Решение:
- 32. Задача Пример. Найти
- 33. Задача Пример. Найти Решение:
- 34. Задача или:
- 35. Интегрирование 3. Метод интегрирования по частям.
- 36. Задача Пример. Найти
- 37. Задача Пример. Найти Решение:
- 38. Задача Пример. Найти Решение:
- 39. Задача
- 40. Интегрирование 4. Интегрирование функций вида:
- 41. Интегрирование 1. В числителе дроби
- 42. Задача Пример. Найти
- 43. Задача Решение:
- 44. Задача Пример. Найти
- 45. Задача Решение:
- 46. Интегрирование 5. Интегрирование дробно-рациональных функций.
- 47. Интегрирование Разложение дробей в простейшие:
- 48. Интегрирование 3. В знаменателе имеются комплексные корни:
- 49. Задача Пример. Найти
- 50. Задача Решение:
- 51. Задача
- 52. Задача
- 53. Задача
- 54. Задача Пример. Найти
- 55. Задача Решение:
- 56. Задача Решение:
- 57. Задача
- 58. Задача
- 59. Интегрирование 6. Тригонометрические подстановки.
- 60. Задача Пример. Найти
- 61. Задача Решение:
- 62. Задача Пример. Найти
- 63. Задача Решение:
- 64. Интегрирование Рассмотрим задачу о вычислении
- 65. Интегрирование
- 66. Интегрирование Сумма такого вида называется
- 67. Интегрирование
- 68. Интегрирование Геометрический смысл определённого интеграла.
- 69. Интегрирование
- 70. Интегрирование Теорема (достаточное условие интегрируемости
- 71. Интегрирование Свойства определённого интеграла. Если
- 72. Интегрирование 5. 6. Если верхний
- 73. Интегрирование 8. Если верхний предел интегрирования больше
- 74. Интегрирование 9. (Теорема о среднем) Если верхний
- 75. Интегрирование Интеграл вида
- 76. Интегрирование Теорема. Пусть функция
- 77. Интегрирование Теорема. Пусть функция
- 78. Интегрирование Теорема. Пусть функции u=u(x),
- 79. Интегрирование
- 80. Интегрирование
- 81. Интегрирование
- 82. Интегрирование
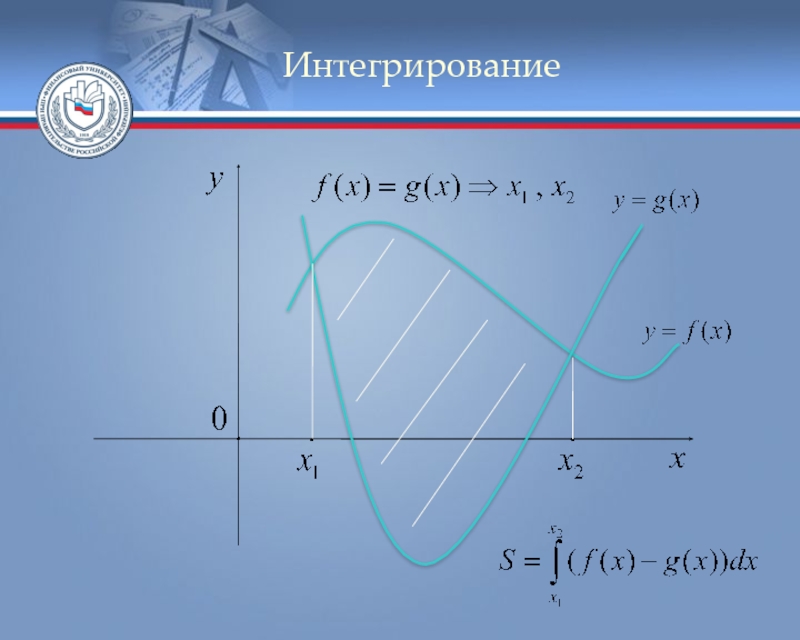
- 83. Интегрирование С помощью определённого интеграла
- 84. Задача Пример. Найти площадь фигуры,
- 85. Задача
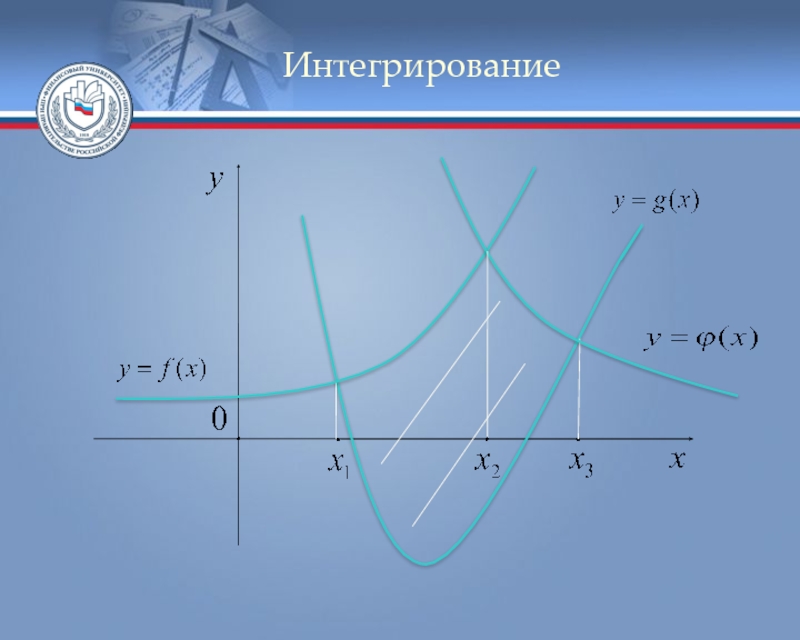
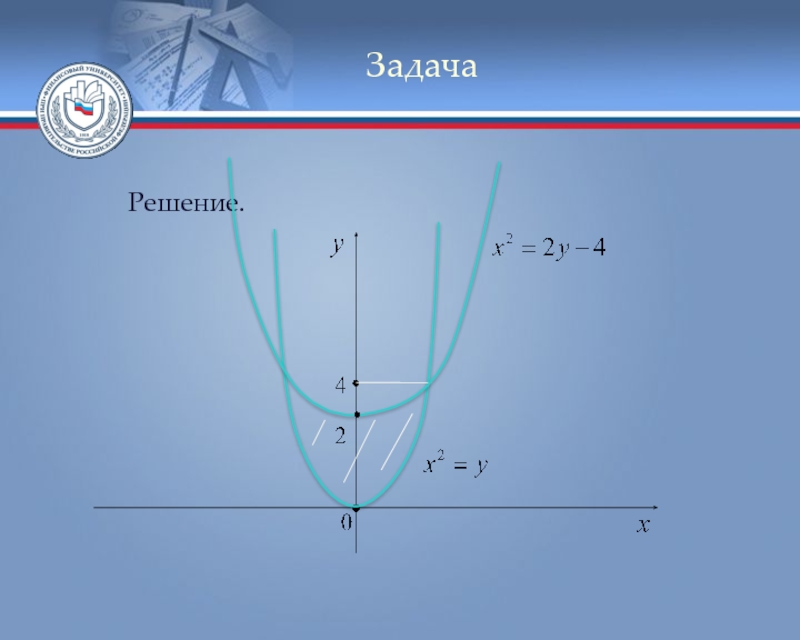
- 86. Задача Пример. Найти площадь фигуры,
- 87. Задача Найдём точки пересечения линий,
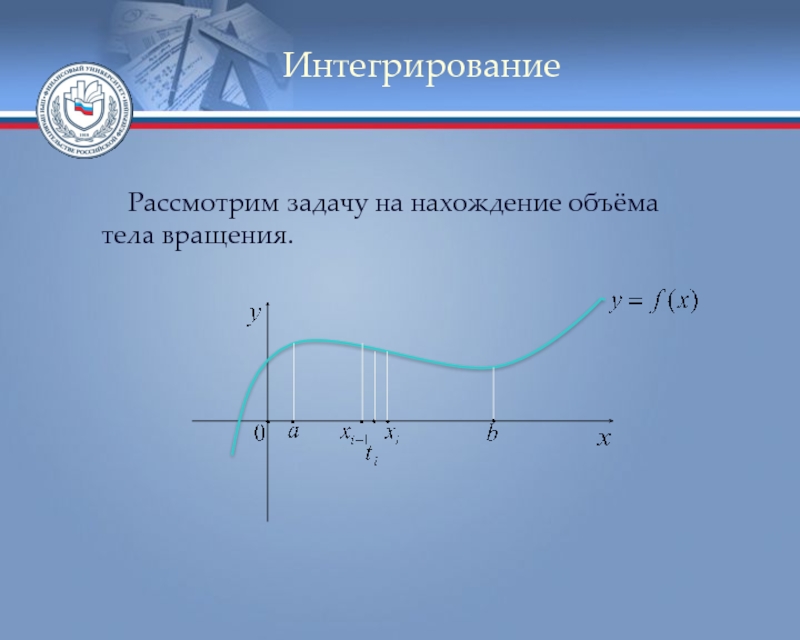
- 88. Интегрирование Рассмотрим задачу на нахождение объёма тела вращения.
- 89. Интегрирование
- 90. Задача Пример. Вычислить объём тела
- 91. Задача Решение.
- 92. Задача
- 93. Задача Пример. Вычислить объём тела
- 94. Задача Решение.
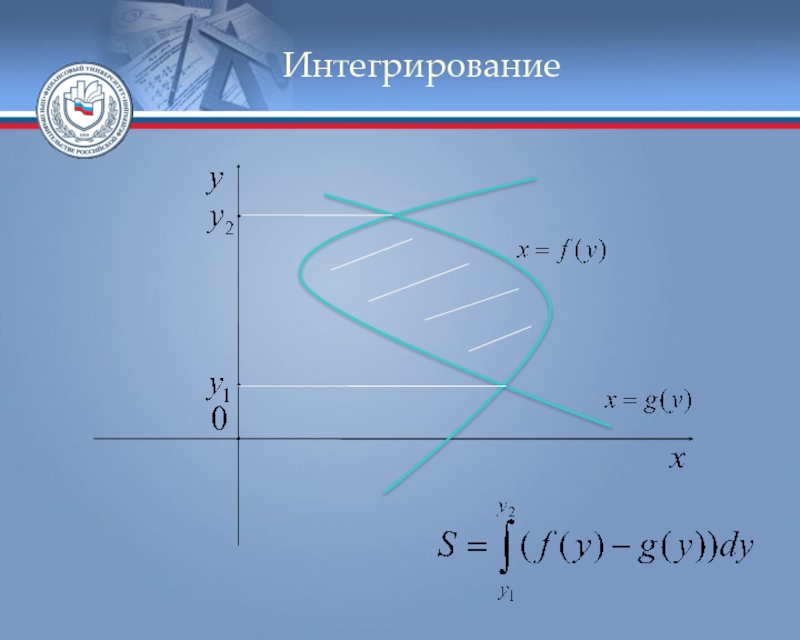
- 95. Задача Решение. Перевыразим x через y.
- 96. Интегрирование Если функция непрерывна на
- 97. Интегрирование В несобственных интегралах следует
- 98. Интегрирование Рассмотрим:
- 99. Интегрирование Если подынтегральная функция имеет
- 100. Интегрирование Если хотя бы один из двух интегралов расходится, то исходный тоже расходится.
- 101. Интегрирование Когда невозможно найти первообразную,
- 102. Задача Пример. Найти Решение:
- 103. Задача Пример. Найти Решение:
- 104. Интегрирование
- 105. Задача Пример. Сходится или расходится
- 106. Задача Решение: Пусть
- 107. Задача Но, пользуясь ответом одной
- 108. Финансовый университет при Правительстве Российской Федерации Конец темы
Функция называется первообразной функцией для функции на множестве Х, если в каждой точке х этого множества справедливо
Слайд 1Финансовый университет
при Правительстве Российской Федерации
Тема №6.
Интегральное исчисление
Слайд 2 Функция называется первообразной
функцией для функции на множестве Х, если в каждой точке х этого множества справедливо равенство
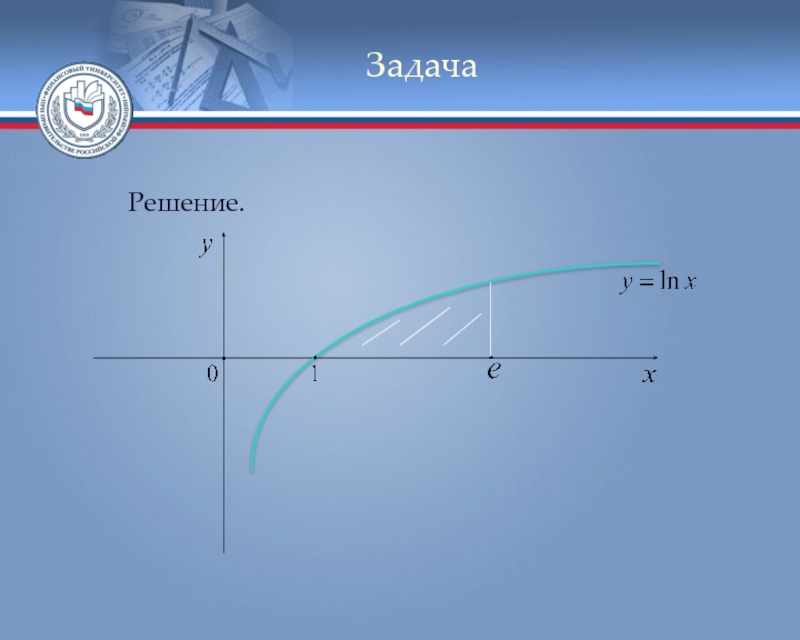
Слайд 3Задача
Например:
Т.о. всякая непрерывная функция имеет бесконечное множество
первообразных, которые отличаются друг от друга постоянным слагаемым.
Слайд 4 Совокупность всех первообразных для функции
на множестве Х называется её неопределённым интегралом и обозначается
выражение, стоящее под знаком дифференциала
Слайд 5Свойства неопределённого интеграла
Производная неопределённого интеграла равна подынтегральной функции, а его дифференциал
равен подынтегральному выражению;
Неопределённый интеграл от дифференциала с точностью до постоянного слагаемого равен выражению, стоящему под знаком дифференциала
Неопределённый интеграл от дифференциала с точностью до постоянного слагаемого равен выражению, стоящему под знаком дифференциала
Слайд 6Свойства неопределённого интеграла
Постоянный множитель можно выносить за знак интеграла
Неопределённый интеграл алгебраической
суммы конечного числа слагаемых равен алгебраической сумме интегралов этих слагаемых
Слайд 7Свойства неопределённого интеграла
Об инвариантности формул интегрирования. Всякая формула интегрирования сохраняет свой
вид при подстановке вместо независимой переменной любой дифференцируемой от неё функции
дифференцируема по х.
дифференцируема по х.
Слайд 12Интегрирование
Рассмотрим некоторые из основных методов интегрирования.
1. Метод разложения интеграла
в сумму интегралов
Слайд 19Задача
2. Метод замены переменной. Метод внесения функции под знак
дифференциала.
Пример. Найти
Пример. Найти
Слайд 23Задача
Можно использовать вместо замены переменной метод внесения функции под знак
дифференциала, используя:
Решение:
Решение:
Слайд 41Интегрирование
1. В числителе дроби выделить производную
2. Разложить
подынтегральную функцию на два слагаемых;
3. Один из интегралов (первый) решается заменой или внесением под знак дифференциала, другой выделением полного квадрата в знаменателе.
3. Один из интегралов (первый) решается заменой или внесением под знак дифференциала, другой выделением полного квадрата в знаменателе.
Слайд 46Интегрирование
5. Интегрирование дробно-рациональных функций.
Сначала выделить целую
часть дроби (если эта дробь неправильная, у которой степень числителя больше или равна степени знаменателя). Затем разложить дробь в сумму простейших дробей (у которых знаменатель не раскладывается на рациональные множители). Применить «метод неопределённых коэффициентов».
Слайд 47Интегрирование
Разложение дробей в простейшие:
Корни знаменателя действительные и различные:
Корни знаменателя
кратные:
Слайд 59Интегрирование
6. Тригонометрические подстановки.
В интегралах, содержащих
Можно использовать тангенсную подстановку:
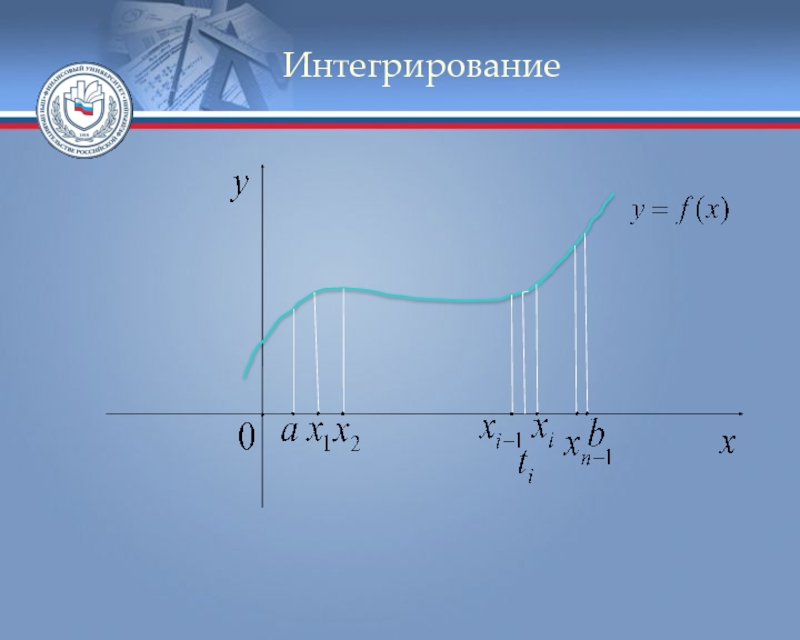
Слайд 64Интегрирование
Рассмотрим задачу о вычислении площади криволинейной трапеции: Пусть на
отрезке [a; b] задана неотрицательная функция
Найдём площадь криволинейной трапеции, ограниченной линиями:
Разобьём отрезок на n частичных интервалов точками Обозначим
На каждом из полученных интервалов выберем некоторую точку
Найдём площадь криволинейной трапеции, ограниченной линиями:
Разобьём отрезок на n частичных интервалов точками Обозначим
На каждом из полученных интервалов выберем некоторую точку
Слайд 66Интегрирование
Сумма такого вида называется интегральной суммой для функции
на отрезке [a; b].
Пусть существует конечный предел интегральной суммы, который не зависит от способа выбора точек при стремлении к нулю длины наибольшего частичного интервала, тогда этот предел называется определённым интегралом (по Риману) от функции на отрезке [a; b].
Пусть существует конечный предел интегральной суммы, который не зависит от способа выбора точек при стремлении к нулю длины наибольшего частичного интервала, тогда этот предел называется определённым интегралом (по Риману) от функции на отрезке [a; b].
Слайд 67Интегрирование
При этом число a называется нижним, число
b – верхним пределами интегрирования соответственно.
Слайд 68Интегрирование
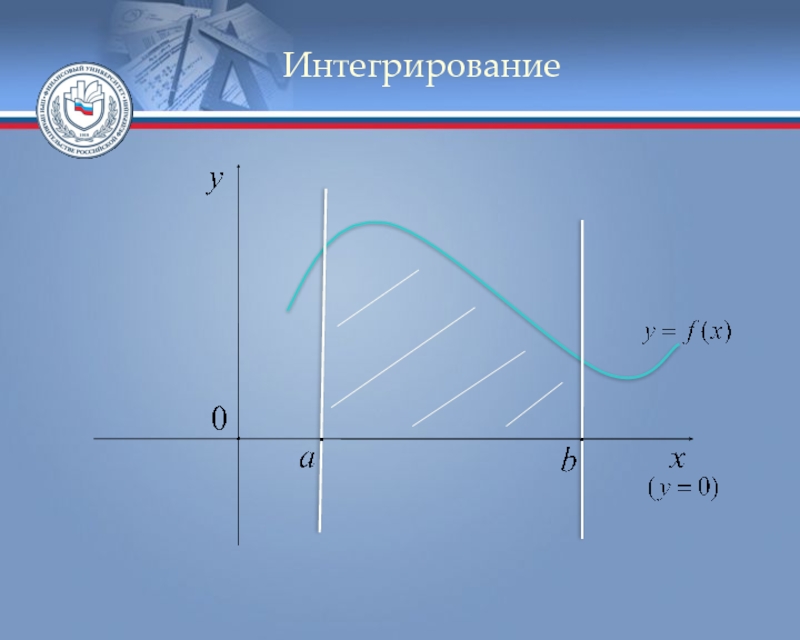
Геометрический смысл определённого интеграла. Если функция
непрерывна и неотрицательна на отрезке
То численно равен площади
криволинейной трапеции , ограниченной линиями
То численно равен площади
криволинейной трапеции , ограниченной линиями
Слайд 70Интегрирование
Теорема (достаточное условие интегрируемости функции): Если функция непрерывна на
некотором отрезке, то она на этом отрезке интегрируема (т.е. существует её определённый интеграл).
Слайд 71Интегрирование
Свойства определённого интеграла.
Если верхний и нижний пределы интегрирования совпадают,
то интеграл равен нулю.
Если верхний и нижний пределы интегрирования поменять местами, то изменится знак интеграла.
Постоянный множитель можно выносить за знак интеграла.
Интеграл алгебраической суммы конечного числа слагаемых равен алгебраической сумме интегралов этих слагаемых.
Если верхний и нижний пределы интегрирования поменять местами, то изменится знак интеграла.
Постоянный множитель можно выносить за знак интеграла.
Интеграл алгебраической суммы конечного числа слагаемых равен алгебраической сумме интегралов этих слагаемых.
Слайд 72Интегрирование
5.
6. Если верхний предел интегрирования больше нижнего и подынтегральная функция знакопостоянна,
то определённый интеграл имеет тот же знак, что и функция.
7. Если верхний предел интегрирования больше нижнего и
7. Если верхний предел интегрирования больше нижнего и
Слайд 73Интегрирование
8. Если верхний предел интегрирования больше нижнего и
где m и M
– некоторые числа.
Слайд 74Интегрирование
9. (Теорема о среднем) Если верхний предел интегрирования больше нижнего и
подынтегральная функция непрерывна на отрезке интегрирования, то внутри этого отрезка найдётся такая точка с, для которой справедливо равенство:
Слайд 75Интегрирование
Интеграл вида
называется
интегралом с переменным верхним пределом.
Теорема: Пусть функция непрерывна на некотором отрезке. Тогда в каждой точке х этого отрезка производная интеграла с переменным верхним пределом этой функции по её верхнему пределу равна подынтегральной функции.
интегралом с переменным верхним пределом.
Теорема: Пусть функция непрерывна на некотором отрезке. Тогда в каждой точке х этого отрезка производная интеграла с переменным верхним пределом этой функции по её верхнему пределу равна подынтегральной функции.
Слайд 76Интегрирование
Теорема. Пусть функция
непрерывна на отрезке [a; b] и F(x) – любая её первообразная для на этом отрезке. Тогда определённый интеграл от этой функции равен приращению первообразной на этом отрезке.
Это формула Ньютона – Лейбница.
Это формула Ньютона – Лейбница.
Слайд 77Интегрирование
Теорема. Пусть функция имеет
непрерывную производную на отрезке [c; d], a=g(c), b=g(d) и функция непрерывна в каждой точке х вида х= g(t), где t принадлежит отрезку [c; d]. Тогда справедливо равенство:
Эта формула называется формулой замены переменной в определённом интеграле.
Эта формула называется формулой замены переменной в определённом интеграле.
Слайд 78Интегрирование
Теорема. Пусть функции u=u(x), v=v(x) имеют непрерывные производные на
отрезке [a; b]. Тогда
Эта формула называется формулой интегрирования по частям в определённом интеграле.
Эта формула называется формулой интегрирования по частям в определённом интеграле.
Слайд 83Интегрирование
С помощью определённого интеграла можно находить площади плоских фигур,
объёмы тел вращения, объёмы тел, полученных сечением плоскостями, площади поверхностей, длины дуг линий, центр масс фигур (в физике) и т.д. Рассмотрим некоторые из этих задач.
Слайд 87Задача
Найдём точки пересечения линий, которые в свою очередь будут
пределами интегрирования.
Слайд 90Задача
Пример. Вычислить объём тела вращения вокруг оси абсцисс фигуры,
ограниченной линиями y=lnx, y=0, x=1, x=e.
Слайд 93Задача
Пример. Вычислить объём тела вращения вокруг оси ординат фигуры,
ограниченной линиями
Слайд 96Интегрирование
Если функция непрерывна на
, то
интеграл вида называется
несобственным интегралом первого рода.
Аналогично
интеграл вида называется
несобственным интегралом первого рода.
Аналогично
Слайд 97Интегрирование
В несобственных интегралах следует осуществлять предельный переход:
Если предел конечен, то интеграл называется сходящимся. Если бесконечен или не существует, то он является расходящимся.
Слайд 98Интегрирование
Рассмотрим:
Если хотя бы один из двух
интегралов расходится, то исходный тоже расходится.
Слайд 99Интегрирование
Если подынтегральная функция имеет разрывы на отрезке интегрирования, то
её интеграл является несобственным второго рода.
, где с – точка
разрыва функции на отрезке [a; b]. Затем в обоих интегралах осуществляем предельные переходы.
, где с – точка
разрыва функции на отрезке [a; b]. Затем в обоих интегралах осуществляем предельные переходы.
Слайд 100Интегрирование
Если хотя бы один из двух интегралов расходится, то исходный тоже
расходится.
Слайд 101Интегрирование
Когда невозможно найти первообразную, можно воспользоваться «признаком сравнения». Пусть
для всех значений х выполняется неравенство тогда:
Слайд 103Задача
Пример. Найти
Решение: Исходный интеграл несобственный второго рода, т.к. функция
терпит разрыв в точке 0.
Интеграл расходится.
Интеграл расходится.
Слайд 106Задача
Решение: Пусть
Обе функции являются бесконечно малыми при х стремящемся
к плюс бесконечности. Сравним их при помощи признака сравнения:
Слайд 107Задача
Но, пользуясь ответом одной из предыдущих задач, имеем
- сходится.
Следовательно, исходный интеграл тоже сходится по признаку сравнения.
Следовательно, исходный интеграл тоже сходится по признаку сравнения.
