Instituto de Física de São Carlos - IFSC
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Modelagem Matemático Computacional FFI0321 презентация
Содержание
- 1. Modelagem Matemático Computacional FFI0321
- 2. Conteúdo do curso Revisão Matemática
- 3. Modelagem matemática e biológica Minimos
- 4. Conteúdo do curso O algoritmo genético
- 5. Critério de avaliação Nota final = 0.5*Média
- 6. Critério de avaliação Duas provas +
- 7. Ambiente de programação: Scilab http://www.scilab.org
- 8. Por que estudar Modelagem Matemático Computacional?
- 9. O que é um modelo matemático? Um
- 10. O que é um modelo matemático-computacional?
- 11. O que é um modelo matemático-computacional? Pendúlo
- 12. Aplicações: Pesquisa científica: Biologia: Bioinformática Biologia
- 13. Desenvolvimento tecnológico Engenharia Aeronaves Automobilismo Mercado financeiro
- 14. Biologia de sistemas Dobramento de proteínas O
- 15. Sistemas não-lineares Teoria do Caos Turbulência Atrator de Lorentz
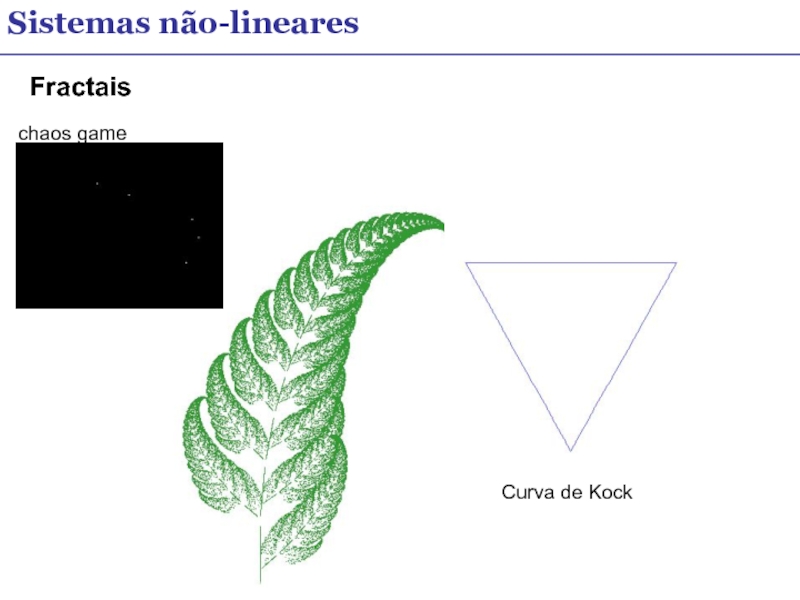
- 16. Fractais Sistemas não-lineares Curva de Kock chaos game
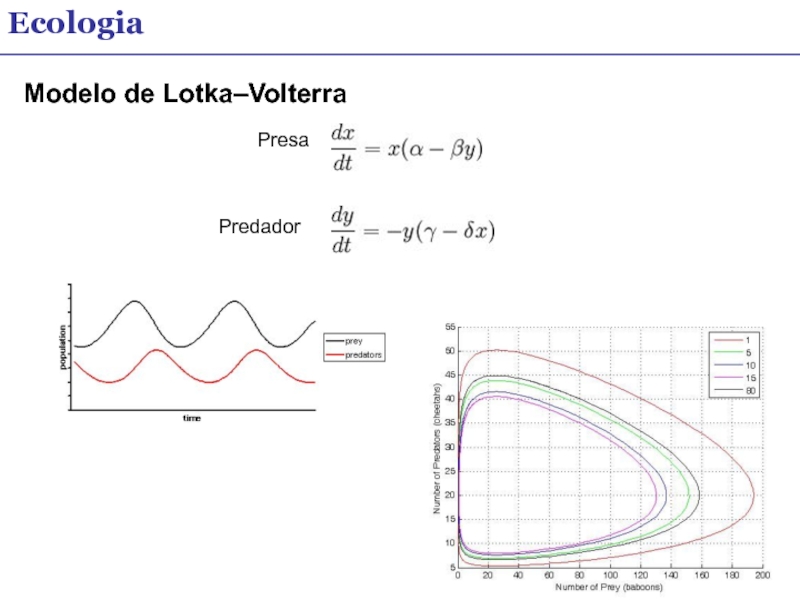
- 17. Ecologia Modelo de Lotka–Volterra Presa Predador
- 18. Aulas Teoria Segunda-feira: sala 149 Quinta-feira: Anfi-verde Prática Sala 206
- 19. Bibliografia L. da F. Costa e R.
Conteúdo do curso Revisão Matemática Funções reais Funções complexas Algebra linear Geometria diferencial Cálculo multivariado Convolução e correlação Probabilidade e estatística
Слайд 1Modelagem Matemático Computacional
FFI0321
Universidade de São Paulo - USP
Instituto de Física de
São Carlos
Слайд 2Conteúdo do curso
Revisão Matemática
Funções reais
Funções complexas
Algebra linear
Geometria diferencial
Cálculo multivariado
Convolução e correlação
Probabilidade e estatística
Cálculo multivariado
Convolução e correlação
Probabilidade e estatística
Слайд 3 Modelagem matemática e biológica
Minimos quadráticos generalizados e suas aplicações
Solução numérica de equações diferenciais parciais
Solução numérica de equações diferenciais ordinárias
As transformadas de Hadamard e Fourier
Análise por componentes principais (PCA)
Sistemas aleatórios: Difusão e percolação
Solução numérica de equações diferenciais ordinárias
As transformadas de Hadamard e Fourier
Análise por componentes principais (PCA)
Sistemas aleatórios: Difusão e percolação
Conteúdo do curso
Слайд 4Conteúdo do curso
O algoritmo genético
Campos e potenciais
Ondas
Dinâmica
de populações
Equações de reação e difusão
Sistemas de partículas
Dobramento de proteínas
Equações de reação e difusão
Sistemas de partículas
Dobramento de proteínas
Слайд 5Critério de avaliação
Nota final = 0.5*Média das provas +
0.4*Média dos
projetos +
0.1*Média das listas de exercícios
Freqüência < 70% = Reprovado!
Conteúdo:
~ 60% aulas teóricas
~ 40% laboratório (Scilab)
Слайд 6Critério de avaliação
Duas provas + 1 substitutiva
Avaliações dos projetos
em 2 etapas
Listas serão disponibilizadas no site periodicamente
Listas serão disponibilizadas no site periodicamente
Site da disciplina
http://cyvision.if.sc.usp.br/~francisco/modelagem
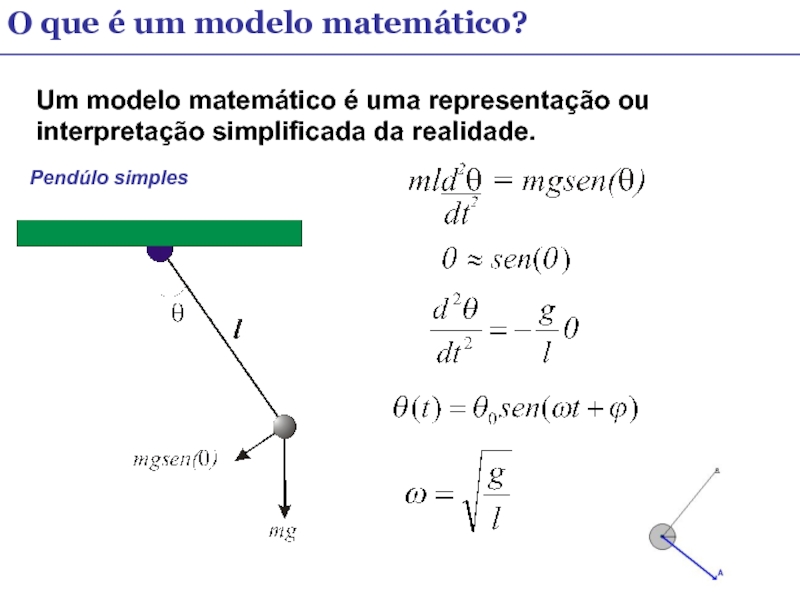
Слайд 9O que é um modelo matemático?
Um modelo matemático é uma representação
ou interpretação simplificada da realidade.
Pendúlo simples
Слайд 10O que é um modelo matemático-computacional?
A modelagem computacional é a
área que trata da simulação de soluções para problemas científicos, analisando os fenômenos, desenvolvendo modelos matemáticos para sua descrição, e elaborando códigos computacionais para obtenção daquelas soluções.
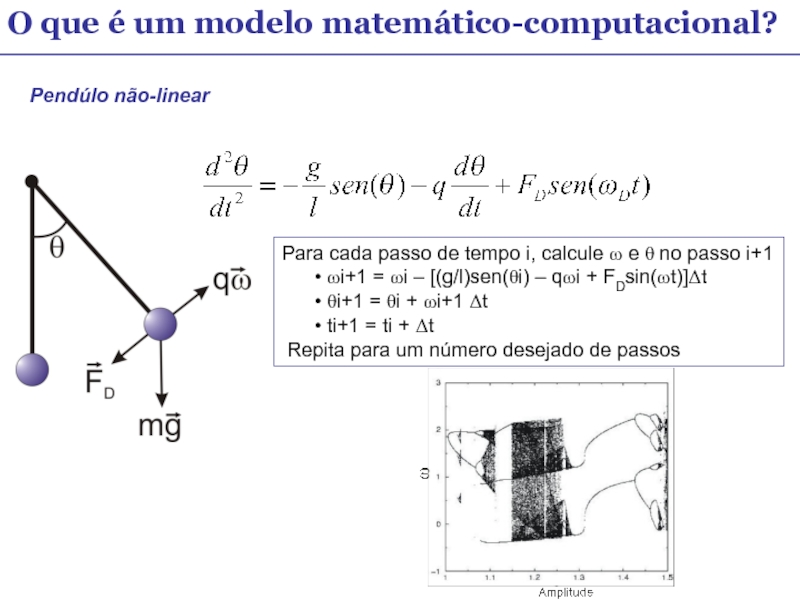
Слайд 11O que é um modelo matemático-computacional?
Pendúlo não-linear
Para cada passo de tempo
i, calcule ω e θ no passo i+1
ωi+1 = ωi – [(g/l)sen(θi) – qωi + FDsin(ωt)]Δt
θi+1 = θi + ωi+1 Δt
ti+1 = ti + Δt
Repita para um número desejado de passos
ωi+1 = ωi – [(g/l)sen(θi) – qωi + FDsin(ωt)]Δt
θi+1 = θi + ωi+1 Δt
ti+1 = ti + Δt
Repita para um número desejado de passos
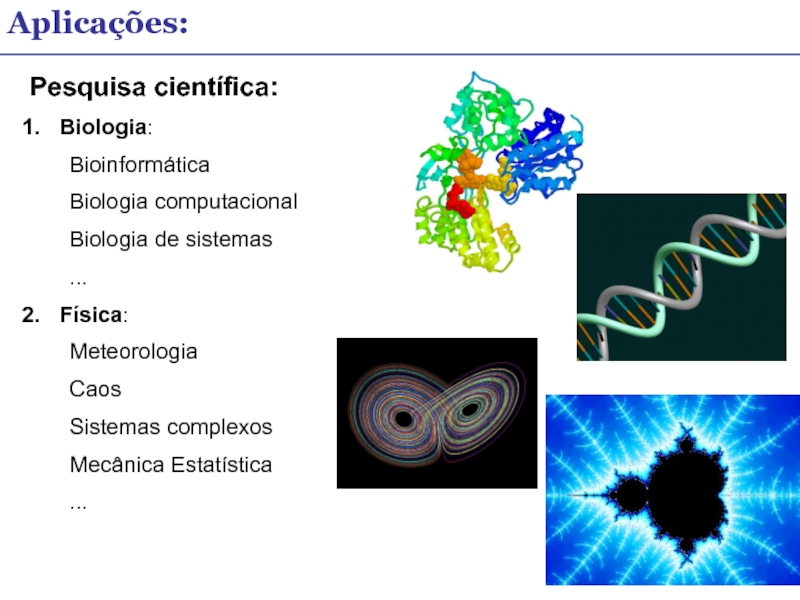
Слайд 12Aplicações:
Pesquisa científica:
Biologia:
Bioinformática
Biologia computacional
Biologia de sistemas
...
Física:
Meteorologia
Caos
Sistemas complexos
Mecânica Estatística
...
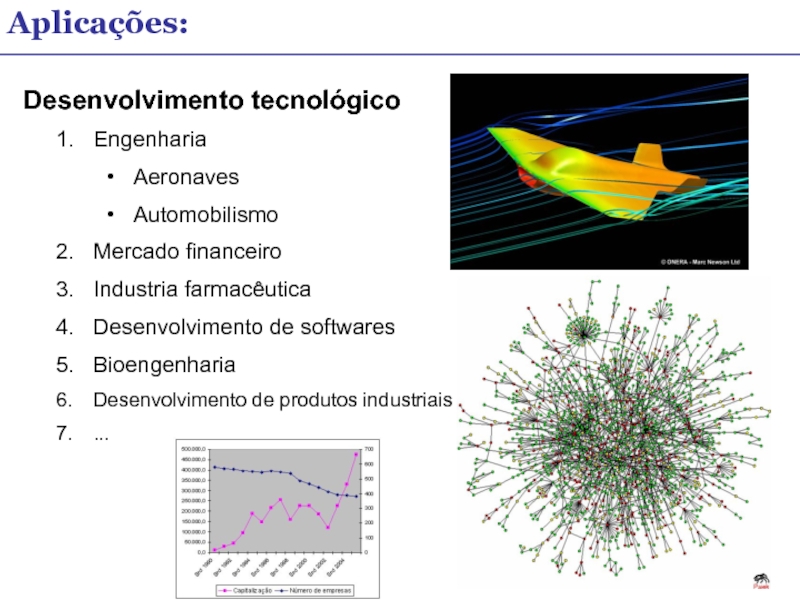
Слайд 13Desenvolvimento tecnológico
Engenharia
Aeronaves
Automobilismo
Mercado financeiro
Industria farmacêutica
Desenvolvimento de softwares
Bioengenharia
Desenvolvimento de produtos industriais
...
Aplicações:
Слайд 14Biologia de sistemas
Dobramento de proteínas
O dobramento de proteínas é um processo
químico através do qual a estrutura de uma proteína assume a sua configuração funcional.
Слайд 19Bibliografia
L. da F. Costa e R. M. Cesar Jr. Shape Analysis
and Classification: Theory and Practice, CRC Press, 2003.
N. J. Giordano. Computational Physics, Prentice-Hall, 1997.
J. M. Cooper. Introduction to Partial Differential Equations with MATLAB, Birkhäuser, 2000.
J. H. Mathews. Numerical Methods for Mathematics, Science and Engineering, Prentice-Hall, 1992.
G. J. Borse. Numerical Methods with MATLAB, PWS Publishing Co., 1997.
http://www.scilab.org
N. J. Giordano. Computational Physics, Prentice-Hall, 1997.
J. M. Cooper. Introduction to Partial Differential Equations with MATLAB, Birkhäuser, 2000.
J. H. Mathews. Numerical Methods for Mathematics, Science and Engineering, Prentice-Hall, 1992.
G. J. Borse. Numerical Methods with MATLAB, PWS Publishing Co., 1997.
http://www.scilab.org
