хаотической динамики и анализ их свойств.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Инструментарий для работы с псевдослучайными последовательностями презентация
Содержание
- 1. Инструментарий для работы с псевдослучайными последовательностями
- 2. Динамический хаос Существуют динамические системы
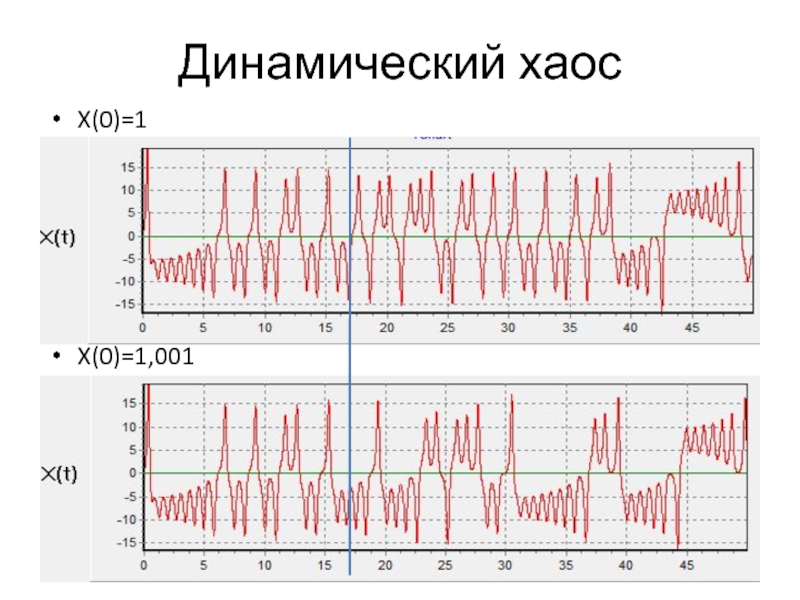
- 3. Динамический хаос X(0)=1 X(0)=1,001
- 4. Постановка задачи Разработать набор программных средств для
- 5. Работа с динамической моделью Для решения
- 6. Расшифровка коэффициентов
- 7. Формирование бинарной последовательности Полученное решение разбивается
- 8. Формирование бинарной последовательности Рассматривается несколько
- 9. Анализ «случайности» построенной последовательности
- 10. Анализ «случайности» построенной последовательности
- 11. Анализ «случайности» построенной последовательности
- 12. Анализ «случайности» построенной последовательности
- 13. Анализ «случайности» построенной последовательности
- 14. Анализ «случайности» построенной последовательности 5) Проверка
- 15. Анализ «случайности» построенной последовательности Если
- 16. Пример
- 17. Численный эксперимент Начальные условия примем такие: X(0)=1;
- 18. Фазовый портрет решения С течением
- 19. Численный эксперимент Решение приведем для X(t):
- 20. Численный эксперимент Для получения более длиной последовательности
- 21. Значения статистик
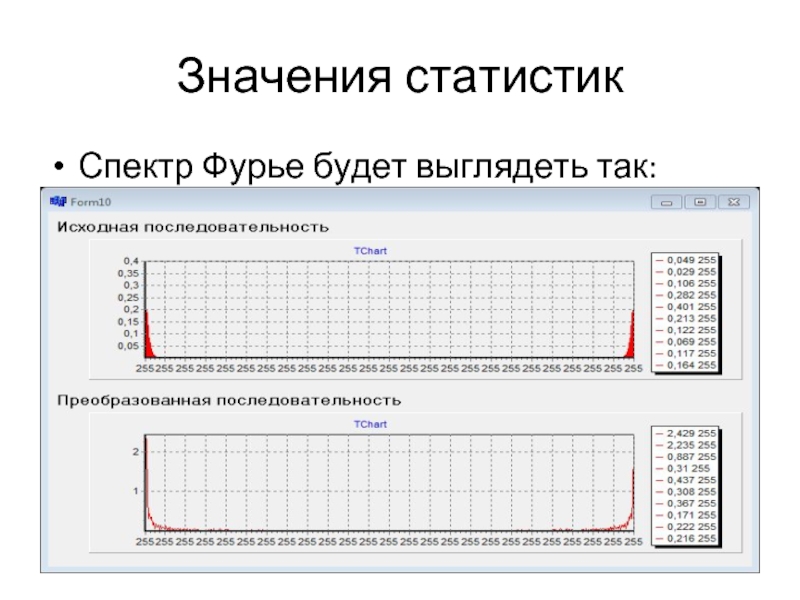
- 22. Значения статистик Спектр Фурье будет выглядеть так:
- 23. Спасибо за внимание
Динамический хаос Существуют динамические системы решение которых обладает хаотическими свойствами.
Слайд 1Инструментарий для
работы с псевдослучайными последовательностями
Генерация псевдослучайных последовательностей на основе моделей
Слайд 2Динамический хаос
Существуют динамические системы
решение которых обладает
хаотическими свойствами.
Слайд 4Постановка задачи
Разработать набор программных средств для
решения системы ОДУ,
генерации на основе получаемых
решений бинарных последовательностей,
анализа статистических свойств полученных последовательностей .
анализа статистических свойств полученных последовательностей .
Слайд 5 Работа с динамической моделью
Для решения системы ОДУ используется метод Рунге-Кутты
4-ого порядка точности.
Слайд 7 Формирование бинарной последовательности
Полученное решение разбивается на отрезки определенной длины.
На каждом
отрезке подсчитывается количество пиков функции-решения.
Если на отрезке количество пиков четно, то в бинарную последовательность добавляется значение 0, если нечетно – 1.
Если на отрезке количество пиков четно, то в бинарную последовательность добавляется значение 0, если нечетно – 1.
Слайд 8 Формирование бинарной последовательности
Рассматривается несколько вариантов определения пиков
1)
2)
3)
Слайд 14Анализ «случайности»
построенной последовательности
5) Проверка спектра Фурье.
Коэффициенты исходной последовательности
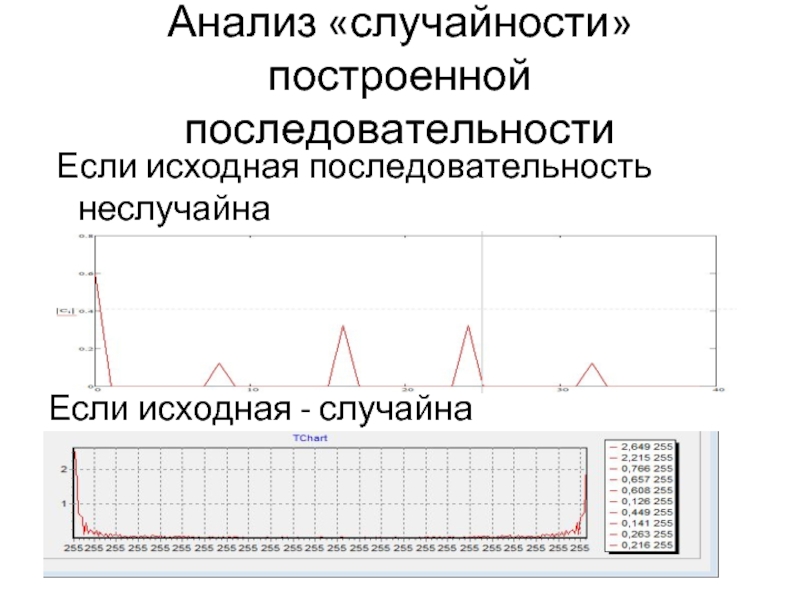
Слайд 15Анализ «случайности»
построенной последовательности
Если исходная последовательность неслучайна
Если исходная - случайна
Слайд 17Численный эксперимент
Начальные условия примем такие:
X(0)=1; Y(0)=1; Z(0)=1;
h=0,01;
(шаг Рунге-Кутты)
n=1000; (количество шагов)
k=10; (количество отрезков слежения)
T0=1;
n=1000; (количество шагов)
k=10; (количество отрезков слежения)
T0=1;
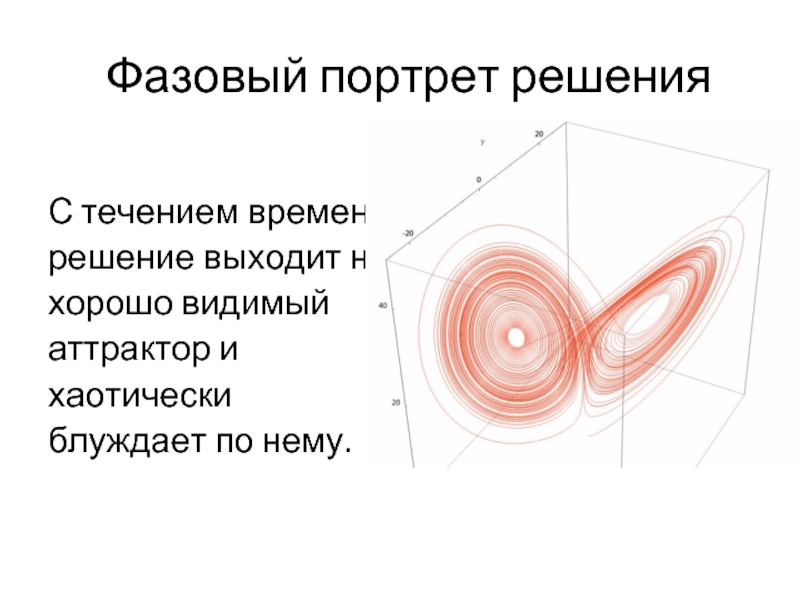
Слайд 18 Фазовый портрет решения
С течением времени
решение выходит на
хорошо видимый
аттрактор
и
хаотически
блуждает по нему.
хаотически
блуждает по нему.
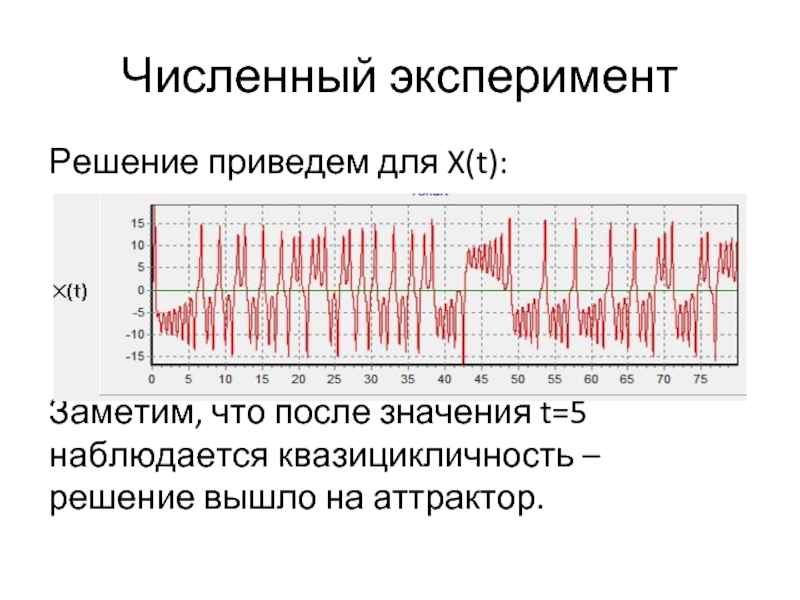
Слайд 19Численный эксперимент
Решение приведем для X(t):
Заметим, что после значения t=5 наблюдается квазицикличность
– решение вышло на аттрактор.
Слайд 20Численный эксперимент
Для получения более длиной последовательности можно продлевать отрезок расчета.
После подсчета
и упрощения получим такую бинарную последовательность:
00001111000011100010000111100111000…
00001111000011100010000111100111000…
