Index of Refraction презентация

Содержание

1. Index of Refraction
2. In uniform isotropic linear media, the wave
3. We can define the index of refraction
4. Let the electric field of optical wave
5. The solution is The induced dipole moment
6. If the second term is small enough
7. The complex refractive index is Normalized plot
8. For more than one resonance frequencies for
9. By definition, We can easily get: Relation Between Dielectric Constant and Refractive Index
10. Real and imaginary part of the index
11. The real part and imaginary part of
12. Typical experimental setup ( 1) halogen lamp;
13. Snell Law become: Reflection of p-polarized light
14. Results Based on Reflection Measurement FIG. 2.
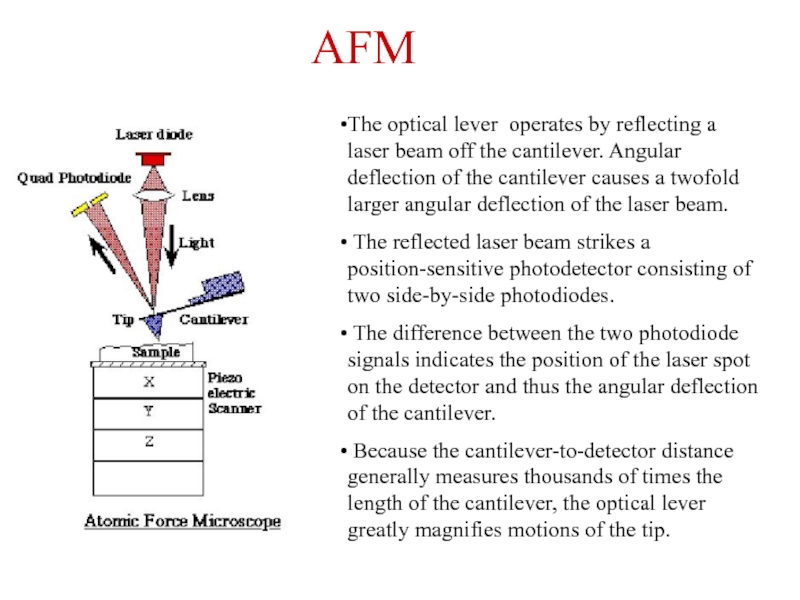
15. Use AFM to Determine the Refractive Index
16. The optical lever operates by reflecting a
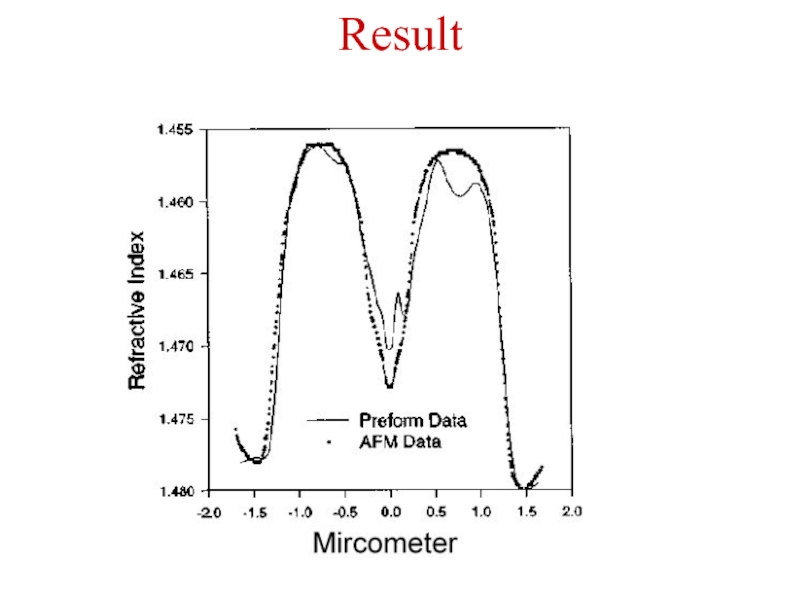
17. Result
18. For θ=0, input wave function a e
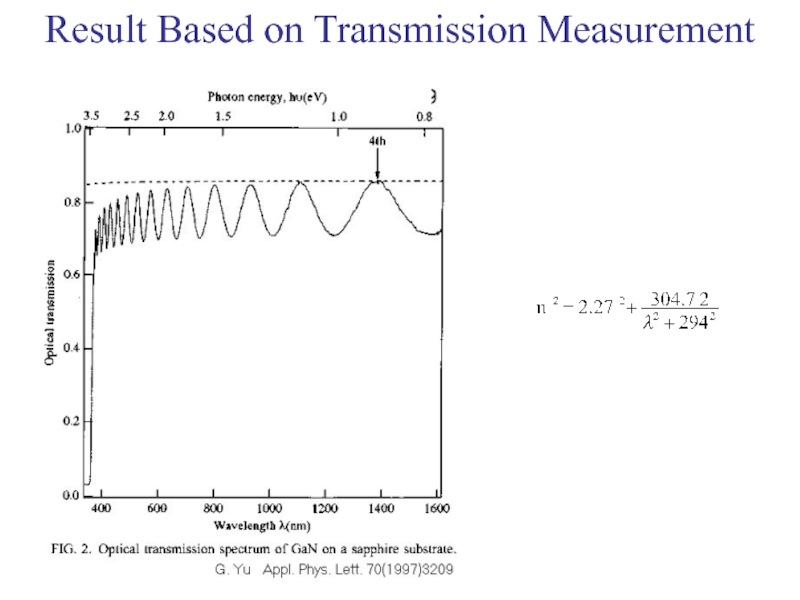
19. Result Based on Transmission Measurement
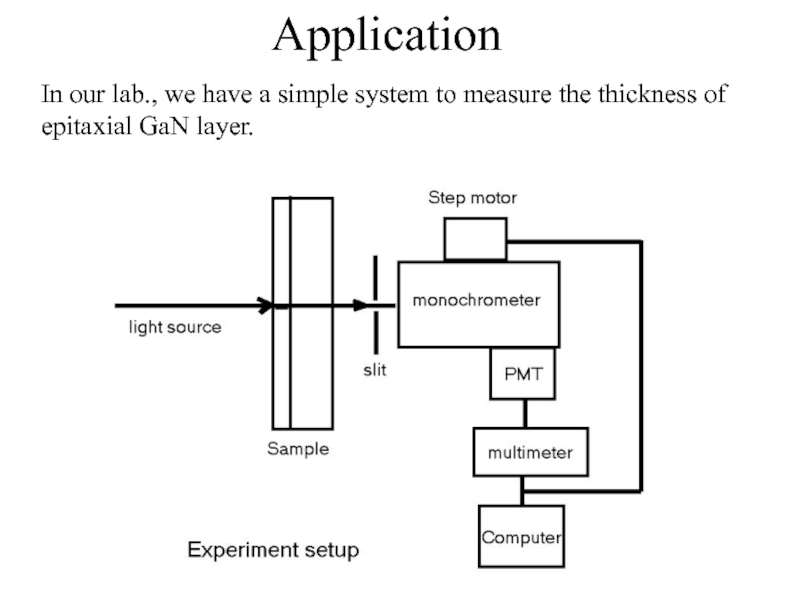
20. Application In our lab., we have a
21. n(λm)=m λm/2d Thickness Measurement Steps to calculate
22. Pochi Yeh, "Optical Wave in Layered

In uniform isotropic linear media, the wave equation is: They are satisfied by plane wave ψ=A e i(k r- ωt) ψ can be any Cartesian components of E and H The

Слайд 1Jing Li
Outline

Introduction
Classical Model
Typical measurement methods
Application
Reference
Index of Refraction

$Jing LiOutlineIntroductionClassical ModelTypical measurement methodsApplicationReferenceIndex of Refraction$

Слайд 2In uniform isotropic linear media, the wave equation is:
They are satisfied

by plane wave
ψ=A e i(k r- ωt)
ψ can be any Cartesian components of E and H
The phase velocity of plane wave travels in the direction of k is

Definition of Index of Refraction

Слайд 3We can define the index of refraction as
Most media are nonmagnetic

and have a magnetic permeability μ=μ0, in this case

In most media, n is a function of frequency.

Definition of Index of Refraction

$We can define the index of refraction asMost media are nonmagnetic and have a magnetic$

Слайд 4Let the electric field of optical wave in an atom be
E=E0e-iωt
the

electron obeys the following equation of motion

X is the position of the electron relative to the atom
m is the mass of the electron
ω0 is the resonant frequency of the electron motion
γ is the damping coefficient

Classical Electron Model ( Lorentz Model)

Слайд 5The solution is
The induced dipole moment is
α is atomic polarizability
The dielectric

constant of a medium depends on the manner in which the atoms are assembled. Let N be the number of atoms per unit volume. Then the polarization can be written approximately as

P = N p = N α E = ε0 χ E

Classical Electron Model ( Lorentz Model)

Слайд 6If the second term is small enough then
The dielectric constant of

the medium is given by
ε = ε0 (1+χ) = ε0 (1+Nα/ ε0)
If the medium is nonmagnetic, the index of refraction is
n= (ε /ε0)1/2 = (1+Nα/ ε0 )1/2

Classical Electron Model ( Lorentz Model)

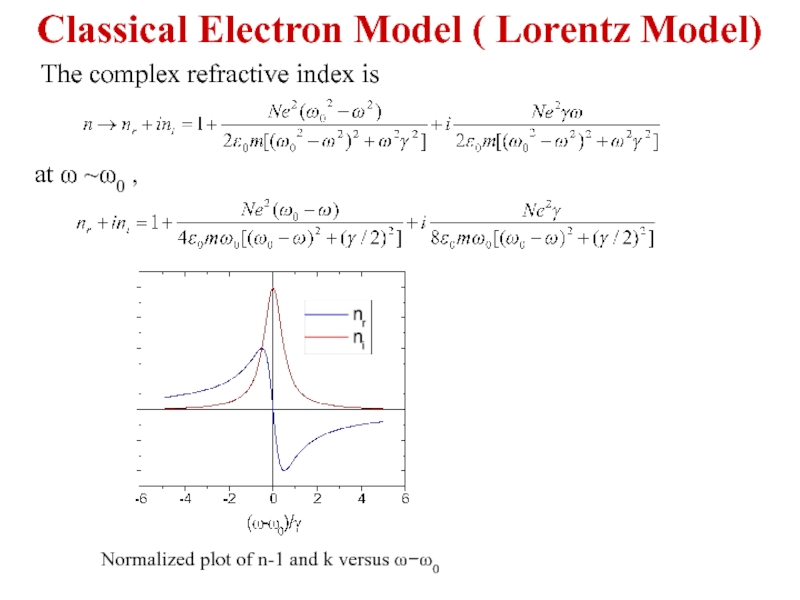
Слайд 7The complex refractive index is
Normalized plot of n-1 and k versus

ω−ω0

at ω ~ω0 ,

Classical Electron Model ( Lorentz Model)

$The complex refractive index isNormalized plot of n-1 and k versus ω−ω0at ω ~ω0 ,Classical$

Слайд 8For more than one resonance frequencies for each atom,
Classical Electron Model

( Drude model)
If we set ω0=0, the Lorentz model become Drude model. This model can be used in free electron metals

Слайд 9By definition,
We can easily get:
Relation Between Dielectric Constant and Refractive Index

$By definition,We can easily get:Relation Between Dielectric Constant and Refractive Index$

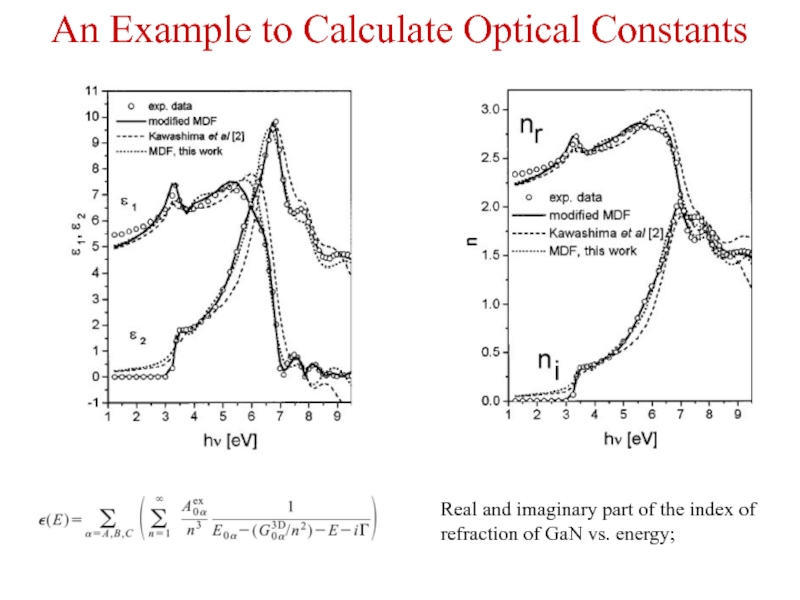
Слайд 10Real and imaginary part of the index of refraction of GaN

vs. energy;

An Example to Calculate Optical Constants

$Real and imaginary part of the index of refraction of GaN vs. energy;An Example to$

Слайд 11The real part and imaginary part of the complex dielectric function

ε (ω) are not independent. they can connected by Kramers-Kronig relations:

P indicates that the integral is a principal value integral.
K-K relation can also be written in other form, like

Kramers-Kronig Relation

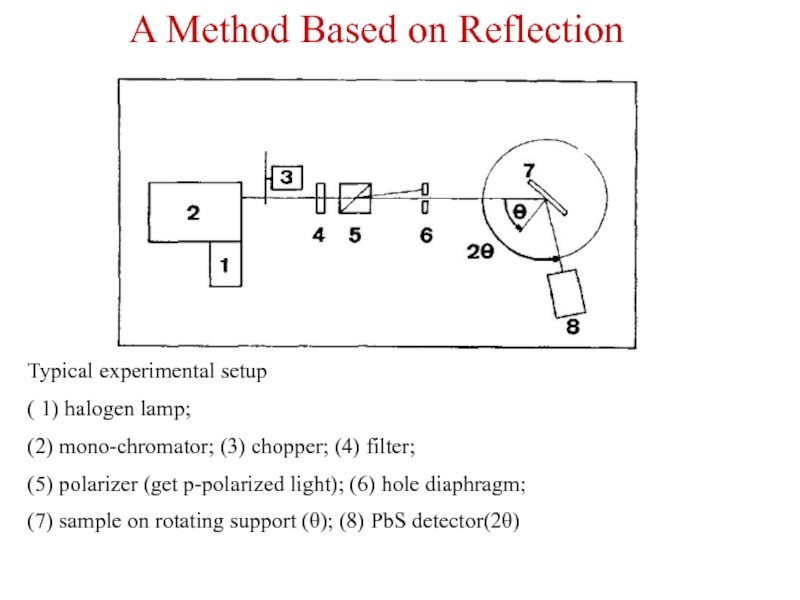
Слайд 12Typical experimental setup
( 1) halogen lamp;
(2) mono-chromator; (3) chopper; (4)

filter;
(5) polarizer (get p-polarized light); (6) hole diaphragm;
(7) sample on rotating support (θ); (8) PbS detector(2θ)

A Method Based on Reflection

Слайд 13Snell Law become:
Reflection of p-polarized light
Reflection coefficient:
In this case, n1=1, and

n2=nr+i n i

Reflectance:
R(θ1, λ, nr, n i)=|r p|2

From this measurement, they got R, θ for each wavelength λ, Fitting the experimental curve, they can get nr and n i .

Calculation

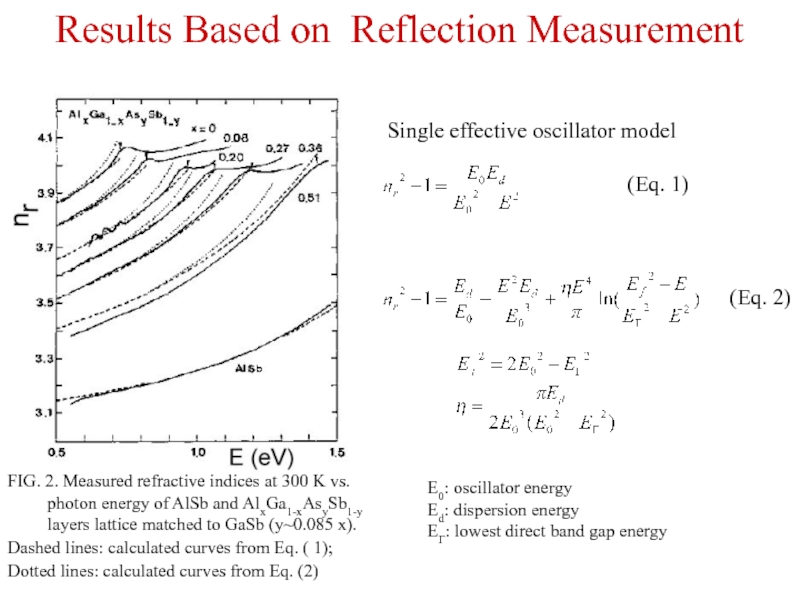
Слайд 14Results Based on Reflection Measurement
FIG. 2. Measured refractive indices at 300

K vs. photon energy of AlSb and AlxGa1-xAsySb1-y layers lattice matched to GaSb (y~0.085 x).
Dashed lines: calculated curves from Eq. ( 1);
Dotted lines: calculated curves from Eq. (2)

E0: oscillator energy
Ed: dispersion energy
EΓ: lowest direct band gap energy

Single effective oscillator model

(Eq. 1)

(Eq. 2)

$Results Based on Reflection MeasurementFIG. 2. Measured refractive indices at 300 K vs. photon energy$

Слайд 15Use AFM to Determine the Refractive Index Profiles of Optical Fibers
Fiber

samples were
Cleaved and mounted in holder
Etched with 5% HF solution
Measured with AFM

There is no way for AFM to measure refractive index directly.
People found fiber material with different refractive index have different etch rate in special solution.

The basic configuration of optical fiber consists of a hair like, cylindrical, dielectric region (core) surrounded by a concentric layer of somewhat lower refractive index( cladding).

$Use AFM to Determine the Refractive Index Profiles of Optical FibersFiber samples wereCleaved and mounted$

Слайд 16The optical lever operates by reflecting a laser beam off the

cantilever. Angular deflection of the cantilever causes a twofold larger angular deflection of the laser beam.
The reflected laser beam strikes a position-sensitive photodetector consisting of two side-by-side photodiodes.
The difference between the two photodiode signals indicates the position of the laser spot on the detector and thus the angular deflection of the cantilever.
Because the cantilever-to-detector distance generally measures thousands of times the length of the cantilever, the optical lever greatly magnifies motions of the tip.

AFM

Слайд 17Result

Слайд 18For θ=0, input wave function a e iφ ,
tm=aTT’R’2m-1 e

i(φ-(2m-1)δ ) (m=1,2…)
δ=2πdn/λ
The transmission wave
function is superposed by all tm
a T = a T T’ e iφ Σ m(R’2m-1 e-i(2m-1)δ )
=(1-R2)a e i(φ−δ) /(1-R2e-i2δ)
(TT’=1-R2 ; R’=-R)
If R<<1, then
a T =a e i(φ−δ)

maximum condition is 2δ=2πm= 4πdn/λ

n(λm)=m λm/2d

A Method Based on Transmission

Слайд 19Result Based on Transmission Measurement

Слайд 20Application
In our lab., we have a simple system to measure the

thickness of epitaxial GaN layer.

Слайд 21n(λm)=m λm/2d
Thickness Measurement
Steps to calculate thickness

Get peak position λm

d=(λm λm-1)/2/[λm-1 n(λm)

− λm n(λm-1)]

Average d

get m min= n(λ max)*2d/ λ max

Calculate d : d=m λm/2/n(λm) (from m min for each peak)

Average d again

Limit
Minimum thickness:~500/n
Error<λ/2n

Слайд 22
Pochi Yeh, "Optical Wave in Layered Media", 1988, John Wiley &

Sons Inc
E. E. Kriezis, D. P. Chrissoulidis & A. G. Papafiannakis, Electromagnetics and Optics, 1992, World Scientific Publishing Co.,
Aleksandra B. Djurisic and E. H. Li, J. OF Appl. Phys., 85 (1999) 2848 (mode for GaN)
C. Alibert, M. Skouri, A. Joullie, M. Benounab andS. Sadiq , J. Appl. Phys., 69(1991)3208 (Reflection)
Kun Liu, J. H. Chu, and D. Y. Tang, J. Appl. Phys. 75 (1994)4176 (KK relation)
G. Yu, G. Wang, H. Ishikawa, M. Umeno, T. Soga, T. Egawa, J. Watanabe, and T. Jimbo, Appl. Phys. Lett. 70 (1997) 3209
Jagat, http://www.phys.ksu.edu/~jagat/afm.ppt (AFM)

Reference

Скачать презентацию

Index of Refraction презентация

Содержание

Слайд 1Jing Li
Outline

Introduction
Classical Model
Typical measurement methods
Application
Reference
Index of Refraction

Слайд 2In uniform isotropic linear media, the wave equation is:
They are satisfied

Слайд 3We can define the index of refraction as
Most media are nonmagnetic

Слайд 4Let the electric field of optical wave in an atom be
E=E0e-iωt
the

Слайд 5The solution is
The induced dipole moment is
α is atomic polarizability
The dielectric

Слайд 6If the second term is small enough then
The dielectric constant of

Слайд 7The complex refractive index is
Normalized plot of n-1 and k versus

Слайд 8For more than one resonance frequencies for each atom,
Classical Electron Model

Слайд 9By definition,
We can easily get:
Relation Between Dielectric Constant and Refractive Index

Слайд 10Real and imaginary part of the index of refraction of GaN

Слайд 11The real part and imaginary part of the complex dielectric function

Слайд 12Typical experimental setup
( 1) halogen lamp;
(2) mono-chromator; (3) chopper; (4)

Слайд 13Snell Law become:
Reflection of p-polarized light
Reflection coefficient:
In this case, n1=1, and

Слайд 14Results Based on Reflection Measurement
FIG. 2. Measured refractive indices at 300

Слайд 15Use AFM to Determine the Refractive Index Profiles of Optical Fibers
Fiber

Слайд 16The optical lever operates by reflecting a laser beam off the

Слайд 17Result

Слайд 18For θ=0, input wave function a e iφ ,
tm=aTT’R’2m-1 e

Слайд 19Result Based on Transmission Measurement

Слайд 20Application
In our lab., we have a simple system to measure the

Слайд 21n(λm)=m λm/2d
Thickness Measurement
Steps to calculate thickness

Get peak position λm

d=(λm λm-1)/2/[λm-1 n(λm)

Слайд 22
Pochi Yeh, "Optical Wave in Layered Media", 1988, John Wiley &

Обратная связь

Что такое ThePresentation.ru?

Index of Refraction презентация

Содержание

Слайд 1Jing LiOutlineIntroductionClassical ModelTypical measurement methodsApplicationReferenceIndex of Refraction

Слайд 2In uniform isotropic linear media, the wave equation is:They are satisfied

Слайд 3We can define the index of refraction asMost media are nonmagnetic

Слайд 4Let the electric field of optical wave in an atom be E=E0e-iωtthe

Слайд 5The solution isThe induced dipole moment isα is atomic polarizabilityThe dielectric

Слайд 6If the second term is small enough thenThe dielectric constant of

Слайд 7The complex refractive index isNormalized plot of n-1 and k versus

Слайд 8For more than one resonance frequencies for each atom,Classical Electron Model

Слайд 9By definition,We can easily get:Relation Between Dielectric Constant and Refractive Index

Слайд 10Real and imaginary part of the index of refraction of GaN

Слайд 11The real part and imaginary part of the complex dielectric function

Слайд 12Typical experimental setup( 1) halogen lamp; (2) mono-chromator; (3) chopper; (4)

Слайд 13Snell Law become:Reflection of p-polarized lightReflection coefficient:In this case, n1=1, and

Слайд 14Results Based on Reflection MeasurementFIG. 2. Measured refractive indices at 300

Слайд 15Use AFM to Determine the Refractive Index Profiles of Optical FibersFiber

Слайд 16The optical lever operates by reflecting a laser beam off the

Слайд 17Result

Слайд 18For θ=0, input wave function a e iφ , tm=aTT’R’2m-1 e

Слайд 19Result Based on Transmission Measurement

Слайд 20ApplicationIn our lab., we have a simple system to measure the

Слайд 21n(λm)=m λm/2dThickness MeasurementSteps to calculate thicknessGet peak position λmd=(λm λm-1)/2/[λm-1 n(λm)

Слайд 22Pochi Yeh, "Optical Wave in Layered Media", 1988, John Wiley &

Похожие презентации

Обратная связь

Что такое ThePresentation.ru?

Слайд 1Jing Li
Outline

Introduction
Classical Model
Typical measurement methods
Application
Reference
Index of Refraction

Слайд 2In uniform isotropic linear media, the wave equation is:
They are satisfied

Слайд 3We can define the index of refraction as
Most media are nonmagnetic

Слайд 4Let the electric field of optical wave in an atom be
E=E0e-iωt
the

Слайд 5The solution is
The induced dipole moment is
α is atomic polarizability
The dielectric

Слайд 6If the second term is small enough then
The dielectric constant of

Слайд 7The complex refractive index is
Normalized plot of n-1 and k versus

Слайд 8For more than one resonance frequencies for each atom,
Classical Electron Model

Слайд 9By definition,
We can easily get:
Relation Between Dielectric Constant and Refractive Index

Слайд 12Typical experimental setup
( 1) halogen lamp;
(2) mono-chromator; (3) chopper; (4)

Слайд 13Snell Law become:
Reflection of p-polarized light
Reflection coefficient:
In this case, n1=1, and

Слайд 14Results Based on Reflection Measurement
FIG. 2. Measured refractive indices at 300

Слайд 15Use AFM to Determine the Refractive Index Profiles of Optical Fibers
Fiber

Слайд 18For θ=0, input wave function a e iφ ,
tm=aTT’R’2m-1 e

Слайд 20Application
In our lab., we have a simple system to measure the

Слайд 21n(λm)=m λm/2d
Thickness Measurement
Steps to calculate thickness

Get peak position λm

d=(λm λm-1)/2/[λm-1 n(λm)

Слайд 22
Pochi Yeh, "Optical Wave in Layered Media", 1988, John Wiley &