- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Хаос в двумерных отображениях презентация
Содержание
- 1. Хаос в двумерных отображениях
- 2. Отображение Эно (Henon map) x, y –
- 3. Уравнение в вариациях для малых отклонений ξ
- 4. Зависимость собственных значений неподвижных точек отображения Эно
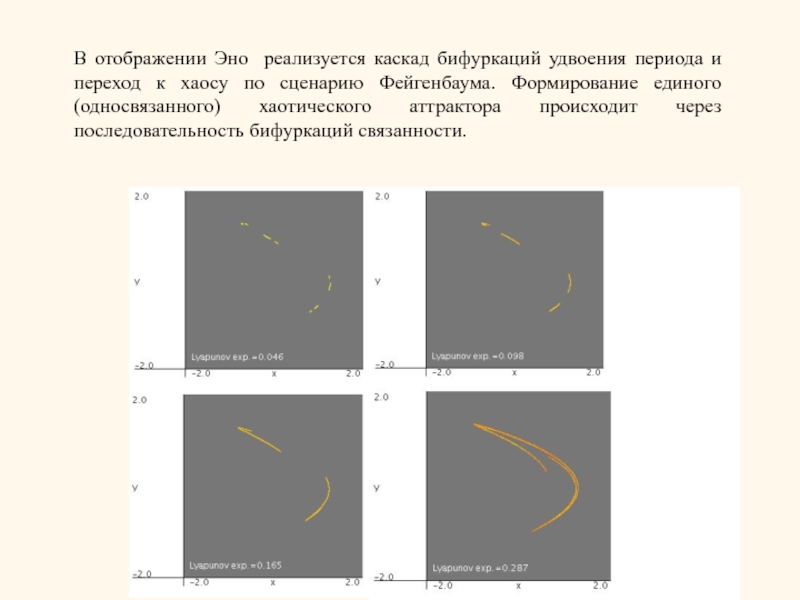
- 5. В отображении Эно реализуется каскад
- 6. Рассмотрим, как на фазовой плоскости происходит формирование
- 7. Изменение площади, или фазового объема, определяется якобианом
- 8. Хаотический аттрактор Эно Общая форма аттрактора повторяет
- 9. Рассмотрим фазовые портреты притягивающих множеств отображения Эно
- 10. Подобно логистическому отображению, в закритической области значений
- 11. Arnold “cat map”: Данное отображение является простой
- 12. Таким образом, отображение «кота» Арнольда представляет собой
- 13. Кубическое отображение Данное отображение было предложено Холмсом
- 14. Связанные логистические отображения α – управляющий параметр
- 15. В зависимости от положения области неопределенности и
Слайд 1Хаос в двумерных отображениях
Двумерные отображения появляются, как правило, при рассмотрении сечения
В отличие от одномерных отображений с хаотической динамикой двумерные отображения могут обладать свойством обратимости, которое служит основой для переноса знаний об их динамике на более широкий класс систем с непрерывным временем. Свойство обратимости означает, что отображение всегда имеет однозначно определенное обратное отображение, или, иными словами, может быть проитерировано в обратном времени произвольное количество раз.
Например, для одномерного логистического отображения данное свойство не выполняется. Любому xn+1 из области значений соответствует два варианта xn .
Слайд 2Отображение Эно (Henon map)
x, y – динамические переменные, μ и b
Неподвижные точки отображения Эно:
Выражения, определяющие координату x*, являются действительными числами при μ > - (1- b)2 /4. Соответственно при этих значениях μ существуют 2 различные неподвижные точки отображения, P1 и P2.
Слайд 3Уравнение в вариациях для малых отклонений ξ и η от состояния
(64)
Собственные числа ρ1 и ρ2 находятся из решения характеристического уравнения
(65)
что дает
для каждой из 2-х неподвижных точек.
Проанализируем характер устойчивости неподвижных точек в зависимости от значения параметра μ. Зафиксируем b = 0.3. При μ → 0 неподвижные точки «разъезжаются» в бесконечность, при этом значения собственных чисел стремятся к для P1 и для P2.
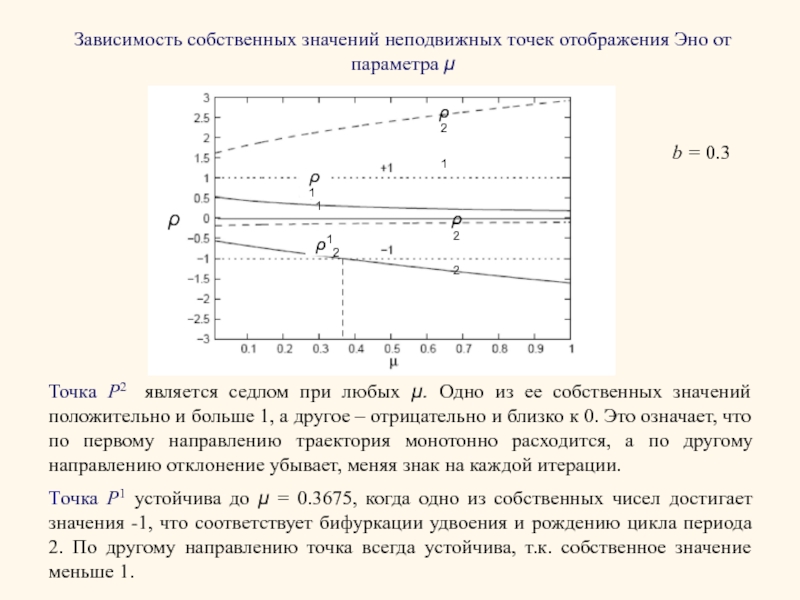
Слайд 4Зависимость собственных значений неподвижных точек отображения Эно от параметра μ
Точка P2
Точка P1 устойчива до μ = 0.3675, когда одно из собственных чисел достигает значения -1, что соответствует бифуркации удвоения и рождению цикла периода 2. По другому направлению точка всегда устойчива, т.к. собственное значение меньше 1.
ρ
ρ21
ρ11
ρ22
ρ12
b = 0.3
Слайд 5
В отображении Эно реализуется каскад бифуркаций удвоения периода и переход к
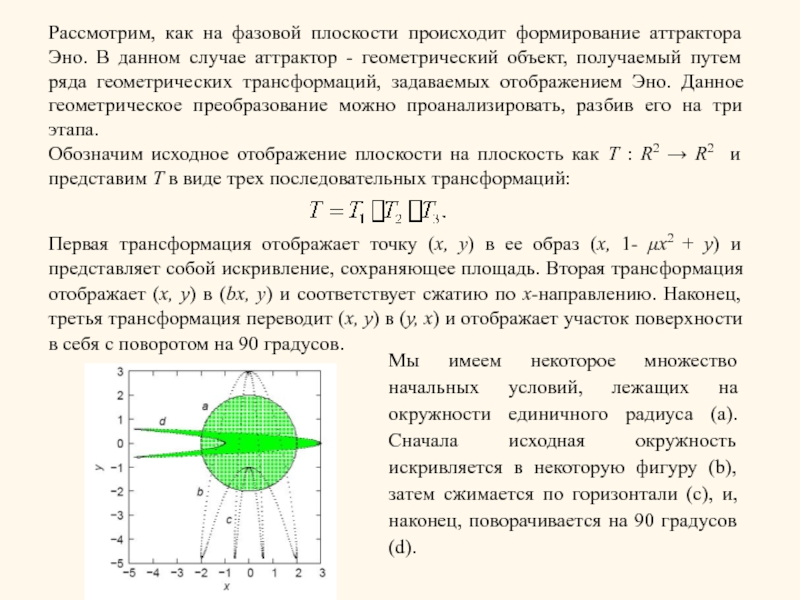
Слайд 6Рассмотрим, как на фазовой плоскости происходит формирование аттрактора Эно. В данном
Обозначим исходное отображение плоскости на плоскость как T : R2 → R2 и представим T в виде трех последовательных трансформаций:
Первая трансформация отображает точку (x, y) в ее образ (x, 1- μx2 + y) и представляет собой искривление, сохраняющее площадь. Вторая трансформация отображает (x, y) в (bx, y) и соответствует сжатию по x-направлению. Наконец, третья трансформация переводит (x, y) в (y, x) и отображает участок поверхности в себя с поворотом на 90 градусов.
Мы имеем некоторое множество начальных условий, лежащих на окружности единичного радиуса (а). Сначала исходная окружность искривляется в некоторую фигуру (b), затем сжимается по горизонтали (c), и, наконец, поворачивается на 90 градусов (d).
Слайд 7Изменение площади, или фазового объема, определяется якобианом
Когда модуль определителя | J
При последовательной итерации отображения Эно повторяющиеся изгибы, сжатия и повороты приводят к формированию на плоскости подковообразного, очень сложно устроенного множества – хаотического аттрактора.
Слайд 8Хаотический аттрактор Эно
Общая форма аттрактора повторяет результат преобразования, рассмотренный выше. Однако
ленный прямоугольником участок, то его структура оказывается геометрически подобна объекту в целом! Увеличение позволяет увидеть мелкие детали и, оказывается, что рассматриваемые участок фазового портрета повторяет сам себя при подходящем масштабировании!
Хаотический аттрактор Эно обладает свойством масштабной инвариантности, что является геометрическим проявлением свойства самоподобия.
Слайд 9Рассмотрим фазовые портреты притягивающих множеств отображения Эно и бассейны их притяжения.
При определенных значениях управляющих параметров отображение Эно может демонстрировать свойство мультистабильности – режим сосуществования двух притягивающих подмножеств на фазовой плоскости. Если менять начальные условия, то наблюдается чередование двух хаотических режимов. Это подтверждает расчет старшего ляпуновского показателя в зависимости от изменения начальной координаты x при фиксированном y. Максимальный показатель случайным образом «скачет» между двумя положительными значениями, свидетельствуя о переходах системы с одного хаотического аттрактора на другой.
Если сравнить эти результаты с видом структуры бассейнов притяжения, то становится понятно, что изменение начальных условий приводит к пересечению границ соответствующих бассейнов.
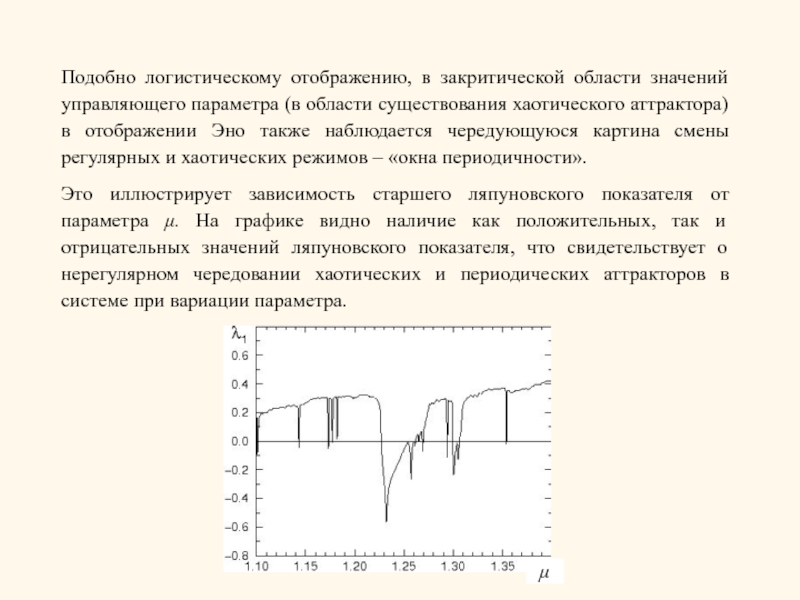
Слайд 10Подобно логистическому отображению, в закритической области значений управляющего параметра (в области
Это иллюстрирует зависимость старшего ляпуновского показателя от параметра μ. На графике видно наличие как положительных, так и отрицательных значений ляпуновского показателя, что свидетельствует о нерегулярном чередовании хаотических и периодических аттракторов в системе при вариации параметра.
μ
Слайд 11Arnold “cat map”:
Данное отображение является простой дискретной системой, которая растягивает и
Фазовое пространство данного отображения может быть представлено квадратом, и процесс растяжения и складывания становится более понятным и явным, если поместить картинку кота в квадрат.
Затем можно видеть эволюцию системы во времени, наблюдая за тем, как кот растягивается, разрезается и затем помещается обратно в квадрат. Из картинки видно, что обычно любые 2 точки, расположенные вначале вблизи друг друга, быстро становятся разделенными друг от друга после повторяющихся применений отображения.
Слайд 12Таким образом, отображение «кота» Арнольда представляет собой преобразование, которое растягивает изображение,
Например, после некоторого числа итераций восстанавливается первоначальное изображение, подвергнутое преобразованию. Говорят, что преобразование Arnold cat map является периодическим с данным числом итераций.
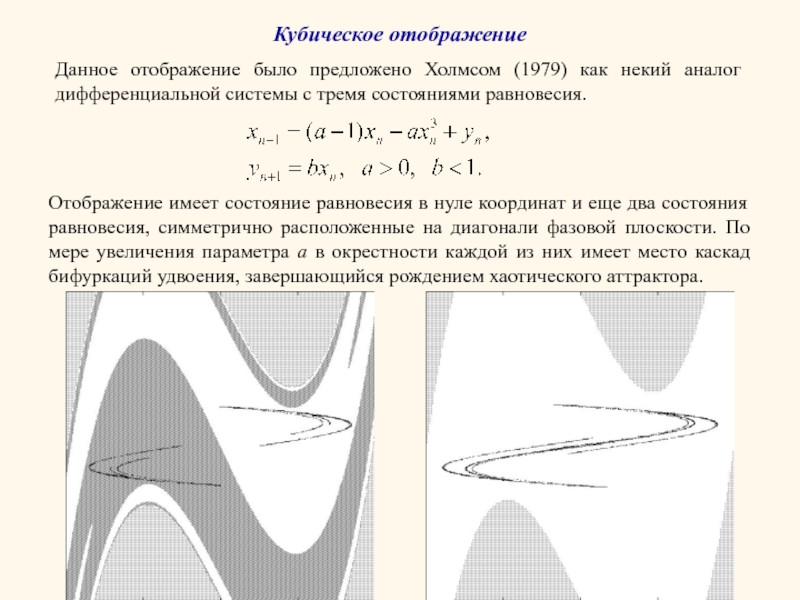
Слайд 13Кубическое отображение
Данное отображение было предложено Холмсом (1979) как некий аналог дифференциальной
Отображение имеет состояние равновесия в нуле координат и еще два состояния равновесия, симметрично расположенные на диагонали фазовой плоскости. По мере увеличения параметра a в окрестности каждой из них имеет место каскад бифуркаций удвоения, завершающийся рождением хаотического аттрактора.
Слайд 14Связанные логистические отображения
α – управляющий параметр системы,
При определенных значениях параметров в системе сосуществуют 3 аттрактора: 1 регулярный и 2 хаотических. Проявляется свойство мультистабильности. Структура бассейнов притяжения фрактальна и изрешеченна. Это ведет к тому, что малая ошибка в задании начальных данных может резко изменить наблюдаемый предельный режим.
Зададим малую область неопределенности по начальным данным в виде квадратика со стороной ε и проитерируем всю эту область в соответствии с отображением.