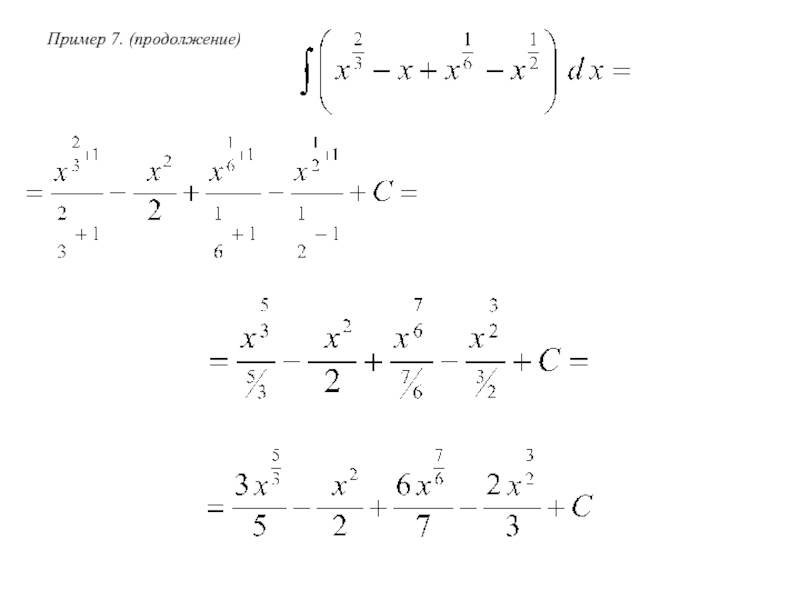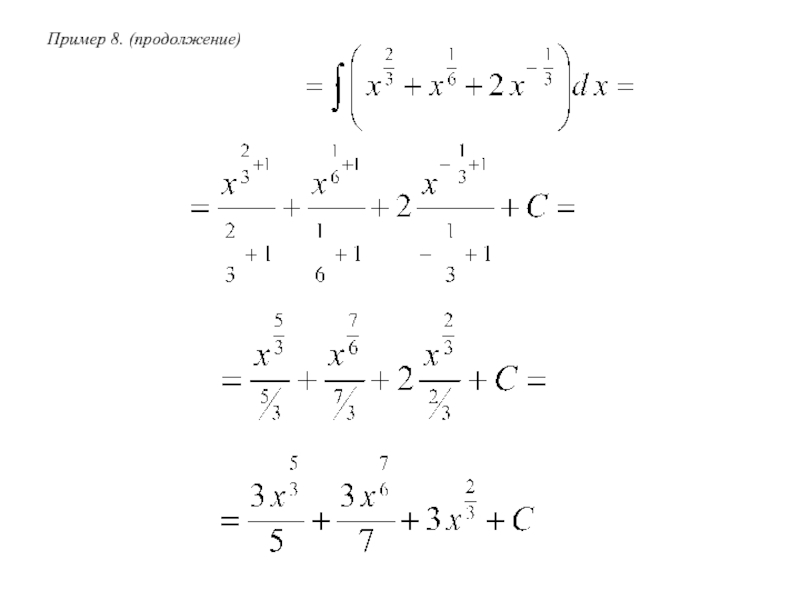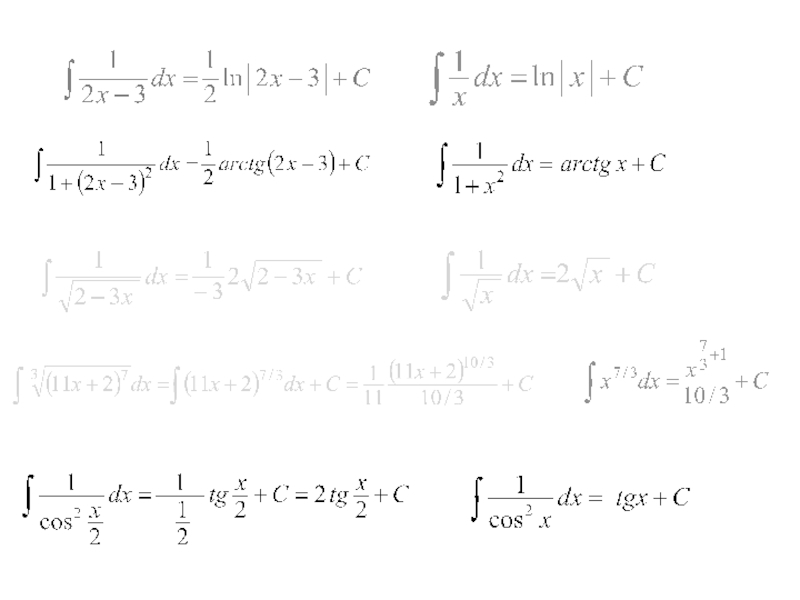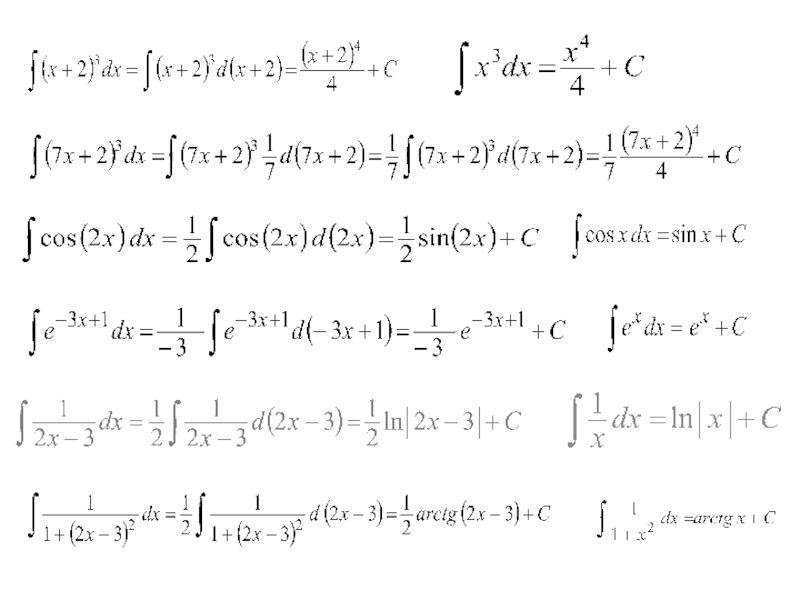- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Непосредственное интегрирование презентация
Содержание
- 1. Непосредственное интегрирование
- 2. ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ НЕПОСРЕДСТВЕННОЕ ИНТЕГРИРОВАНИЕ -
- 3. Пример 6. Найти неопределенный интеграл
- 4. Пример 7. Найти неопределенный интеграл
- 5. Пример 7. (продолжение)
- 6. Пример 8. Найти неопределенный интеграл
- 7. Пример 8. (продолжение)
- 8. Решение. Неопределенный интеграл от суммы или
- 9. 5. Частное правило интегрирования. Это правило упрощает вычисление многих неопределенных интегралов. Например:
- 11. Пример 9. (с использованием частного правила интегрирования)
- 12. 5.1 Другой способ нахождения интегралов вида
- 14. 7. Интегрирование некоторых дробей, содержащих квадратный
- 15. Методическая рекомендация: если в квадратном трехчлене коэффициент
- 16. Практика показывает, что процедура выделения полного квадрата
- 17. Вернемся к интегралу у
- 18. 8. Интегрирование некоторых тригонометрических функций. Тригонометрические формулы,
- 19. Решение. Вызовем нужную тригонометрическую формулу. Вычислим интеграл:
- 20. Пример 14. Найти неопределенный интеграл Решение.
- 21. Пример 15. Найти неопределенный интеграл Решение.
- 22. Степанова Наталия Вадимовна, к.ф.-м. н., доцент кафедры математики ВоГУ ПРЕЗЕНТАЦИЯ ЗАКОНЧЕНА. СПАСИБО ЗА ВНИМАНИЕ.
Слайд 2ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ
НЕПОСРЕДСТВЕННОЕ ИНТЕГРИРОВАНИЕ
- это нахождение интеграла путем преобразования подынтегральной
Слайд 3Пример 6. Найти неопределенный интеграл
Решение.
Вид подынтегральной функции можно менять
с помощью тождественных преобразований !!!
Слайд 4Пример 7. Найти неопределенный интеграл
Решение. Неопределенный интеграл от суммы
равен сумме или разности интегралов.
Но!!!
Неопределенный интеграл от произведения функций не равен произведению интегралов.
Поэтому все тождественные преобразования подынтегральной функции направлены на то, чтобы преобразовать произведение функций в суммы или разности функций. Для этого нужно просто раскрыть скобки.
Слайд 6Пример 8. Найти неопределенный интеграл
Решение. Неопределенный интеграл от
равен сумме или разности интегралов.
Но!!!
Неопределенный интеграл от отношения функций не равен отношению интегралов.
Поэтому все тождественные преобразования подынтегральной функции направлены на то, чтобы преобразовать отношение функций в суммы или разности функций. В данном интеграле для этого нужно просто поделить почленно числитель на знаменатель.
Слайд 8Решение. Неопределенный интеграл от суммы или разности функций
Поэтому все тождественные преобразования данной подынтегральной функции направлены на то, чтобы преобразовать её в суммы или разности функций. Для этого нужно просто раскрыть квадрат суммы.
Слайд 95. Частное правило интегрирования.
Это правило упрощает вычисление многих неопределенных интегралов.
Например:
Слайд 11Пример 9. (с использованием частного правила интегрирования)
Найти неопределенный интеграл
Решение. Частное правило интегрирования позволяет быстрее найти неопределенный интеграл в примере 9.
Для сравнения выпишем результат, полученный ранее.
Слайд 125.1 Другой способ нахождения интегралов вида
Замечание. При частном
Другой способ интегрирования наоборот предполагает преобразование переменной интегрирования х к виду кх+b.
К переменной интегрирования можно прибавлять или вычитать любое число без всяких последствий.
Слайд 147. Интегрирование некоторых дробей, содержащих квадратный трехчлен в знаменателе.
Вспомним процедуру
Пример 10. Найти неопределенный интеграл
Решение.
Слайд 15Методическая рекомендация: если в квадратном трехчлене коэффициент при х2 не равен
Пример 12. Найти неопределенный интеграл
Вычислим интеграл:
Решение. Выпишем только квадратный трехчлен, стоящий под квадратным корнем и выделим в нем полный квадрат.
Слайд 16 Практика показывает, что процедура выделения полного квадрата из квадратного трехчлена очень
Тогда
Решение.
Слайд 17 Вернемся к интегралу у
Использовали табличный интеграл
и частное правило интегрирования
Слайд 188. Интегрирование некоторых тригонометрических функций.
Тригонометрические формулы, используемые при вычислении интегралов.
Универсальная
тригонометрическая
Формулы двойного угла
Слайд 21Пример 15. Найти неопределенный интеграл
Решение. Вызовем подходящую тригонометрическую формулу.
С её
Слайд 22Степанова Наталия Вадимовна,
к.ф.-м. н., доцент кафедры математики ВоГУ
ПРЕЗЕНТАЦИЯ ЗАКОНЧЕНА.
СПАСИБО ЗА ВНИМАНИЕ.
