- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Графические методы оценки параметров распределения презентация
Содержание
- 1. Графические методы оценки параметров распределения
- 2. Оценка параметров распределения графическим методом Нужно
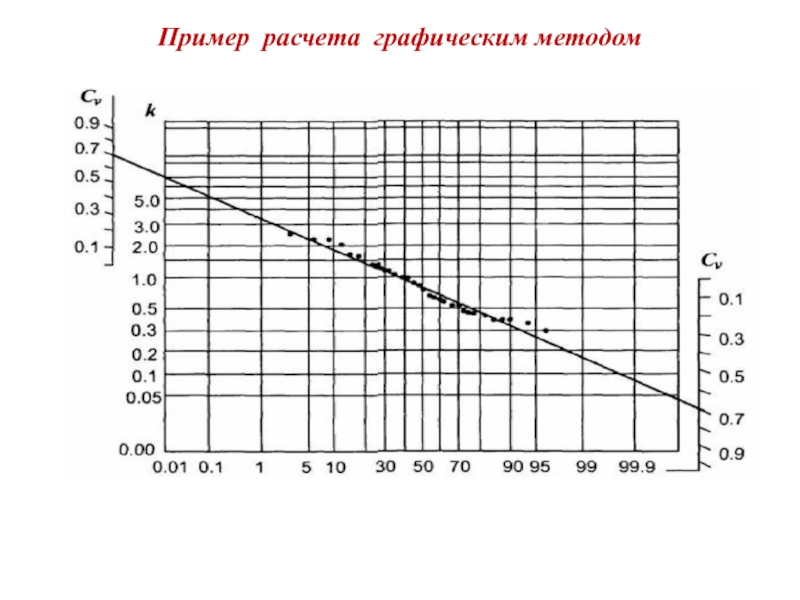
- 3. Пример расчета графическим методом
- 4. Последовательность расчетов графическим методом для
- 5. Последовательность расчетов графическим методом для
- 6. Оценка погрешностей выборочных параметров распределения
- 7. Оценка погрешностей выборочных параметров распределения
- 8. СПАСИБО ЗА ВНИМАНИЕ!
Слайд 2Оценка параметров
распределения графическим методом
Нужно знать заранее вид кривой распределения СВ
Метод
Графический метод
для трехпараметрических кривых распределений
1. На клетчатках с различным значением Cs/Cv строятся эмпирические кривые обеспеченности в модульных коэффициентах
2. В качестве расчетного значения берется соотношение Cs/Cv, при котором на соответствующей клетчатке эмпирическая кривая обеспеченности превращается в прямую линию
3. При этом наклон прямой линии, в которую превращается кривая обеспеченности, зависит от коэффициента вариации. С учетом этого на клетчатке вероятности дополнительно в левом верхнем и правом нижнем углах наносится шкала Cv,
Слайд 4 Последовательность расчетов графическим методом для кривой распределения Крицкого – Менкеля
Дано: Ряд наблюдений за СВ
Требуется: Оценить параметры распределения – хср., σx*, Cv,* Cs* графическим методом для кривой Крицкого – Менкеля
Последовательность расчетов
Рассчитывается Хср
2. По формуле ki = Xi/Xср рассчитываются модульные коэффициенты
3. Ранжируется ряд модульных коэффициентов
4. Рассчитываются ординаты кривой распределения вероятности по формуле
pm = (m/(n + 1))100%
5. На клетчатках, спрямляющих кривую Крицкого – Менкеля, строятся (несколько раз) эмпирические кривые распределения при различных соотношениях Cs/Cv.
Слайд 5 Последовательность расчетов графическим методом для кривой распределения Крицкого – Менкеля
6. В качестве расчетного соотношения Cs/Cv принимается такое соотношение, при котором самым лучшим образом группируются эмпирические точки вдоль прямой линии
7. В поле точек проводится прямая линия и по угловой шкале определяется коэффициент вариации
8. Зная Cv.и зная соотношения Cs/Cv. для данной клетчатки, определяется Cs
9. По формуле Cv*= σx*/хср. определяется СКО.
Двухпараметрический закон распределения
При использовании двухпараметрической кривой распределения вероятности СВ (Пирсона III типа при Cs = 2Cv) используется только одна клетчатка, так как Cs однозначно зависит от Cv. При этом, если эмпирические точки на клетчатке лягут в виде прямой линии, то расчет продолжается по вышеизложенной методике. Если нет, то значить данная двухпараметрическая кривая не подходит аппроксимации закона распределения СВ.
Слайд 6
Оценка погрешностей
выборочных параметров распределения
Оценка параметра распределения некоторой СВ Х сама
Формулы для расчета погрешностей оценок зависят от того, каким методом производилась сама оценка.
Метод моментов
Абсолютная погрешность выборочного среднего определяется по формуле
Относительная погрешность выборочного среднего определяется по формуле