- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теорема Виета. (8 класс) презентация
Содержание
- 1. Теорема Виета. (8 класс)
- 2. Проверка домашней работы №590
- 3. Ответьте на вопросы Как формулируется теорема Виета
- 4. Ответьте на вопросы Как Вы думаете, применима ли теорема Виета для неприведенного квадратного уравнения?
- 5. Решите уравнение Связаны ли корни уравнения с его коэффициентами?
- 6. Ответьте на вопросы Можем ли мы данное
- 7. Ответьте на вопросы После деления на старший
- 8. Теорема Виета для неприведенного квадратного уравнения Пусть
- 9. В геометрии мы сталкивались с тем, что
- 10. Давайте составим обратное утверждение для теоремы Виета
- 11. С помощью теоремы Виета проверим, правильно ли мы нашли корни.
- 12. Решение задач №580 (д,ж) Найдите сумму и
- 13. Решение задач №580 (д,ж) Найдите сумму и
- 14. Решение задач №581 (а) Решите уравнение и
- 15. №583 (а) Найдите подбором корни уравнения:
- 16. Решите самостоятельно №594 (а) Не решая уравнение,
- 17. Домашняя работа п. 23 (теорема Виета, обратная теорема Виета) №580 (е,з), 593, 594(б, д)
Слайд 3Ответьте на вопросы
Как формулируется теорема Виета для
приведенного квадратного уравнения?
Сумма корней
Слайд 4Ответьте на вопросы
Как Вы думаете, применима ли теорема
Виета для неприведенного квадратного
Слайд 6Ответьте на вопросы
Можем ли мы данное уравнение сделать приведенным?
Как?
Поделим уравнение на
Слайд 7Ответьте на вопросы
После деления на старший коэффициент корни уравнения изменятся?
Как называются
Подсказка: для ответа на вопрос обратитесь к учебнику (сведения за 7 класс, раздел «Уравнения», пункт 9)
Можем ли мы теперь применить теорему Виета?
Слайд 8Теорема Виета для неприведенного квадратного уравнения
Пусть квадратное уравнение
имеет корни
Равносильное
Тогда по теореме Виета:
Слайд 9В геометрии мы сталкивались с тем, что для некоторых утверждений будет
Вспомните, как составляются обратные утверждения.
Если данное утверждение сформулировано в виде условного предложения ''если А, то В'', то обратным называется утверждение ''если В, то А'', то есть такое, у которого условием является заключение первого утверждения, а заключением - его же условие.
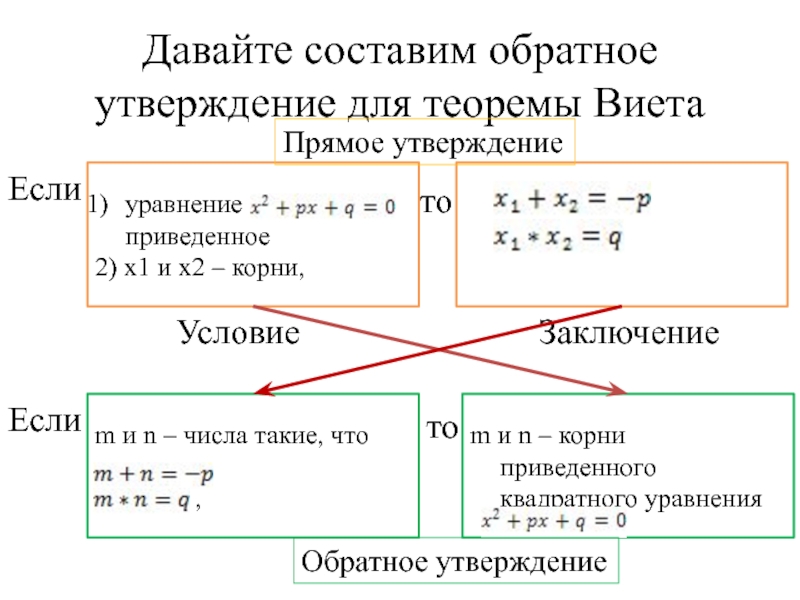
Слайд 10Давайте составим обратное утверждение для теоремы Виета
уравнение
приведенное
2) x1 и x2
Если
то
Условие
Заключение
m и n – числа такие, что
,
m и n – корни приведенного квадратного уравнения
Если
то
Обратное утверждение
Прямое утверждение
Слайд 12Решение задач
№580 (д,ж)
Найдите сумму и произведение корней уравнения:
д)
По теореме Виета для
Ответ: 4,5; -5
Слайд 13Решение задач
№580 (д,ж)
Найдите сумму и произведение корней уравнения:
ж)
По теореме Виета для
Ответ: -1; 0
Слайд 14Решение задач
№581 (а)
Решите уравнение и выполните проверку по теореме, обратной теореме
Найдем дискриминант:
По формуле корней квадратного уравнения получаем:
Покажем, что корни найдены правильно. В данном уравнении
коэффициент p равен -2, а свободный член q равен -9. Тогда:
Значит, по теореме, обратной теореме Виета, эти числа являются
корнями данного квадратного уравнения.
Ответ:
Слайд 15№583 (а)
Найдите подбором корни уравнения:
Дискриминант D=81-4*20 – положительное число. Пусть m
корни уравнения. Тогда
Если m и n – целые числа, то они являются делителями числа 20.
Нужно учесть, что сумма этих чисел равна 9.
10*2
10+2=12
не подходит
-10*(-2)
-10-2=-12
не подходит
-5*(-4)
-5-4=-9
не подходит
5*4
5+4=9
подходит
Ответ: 5; 4
Слайд 16Решите самостоятельно
№594 (а)
Не решая уравнение, выясните, имеет ли оно корни, и
Указание: для определения знаков воспользуйтесь теоремой Виета.