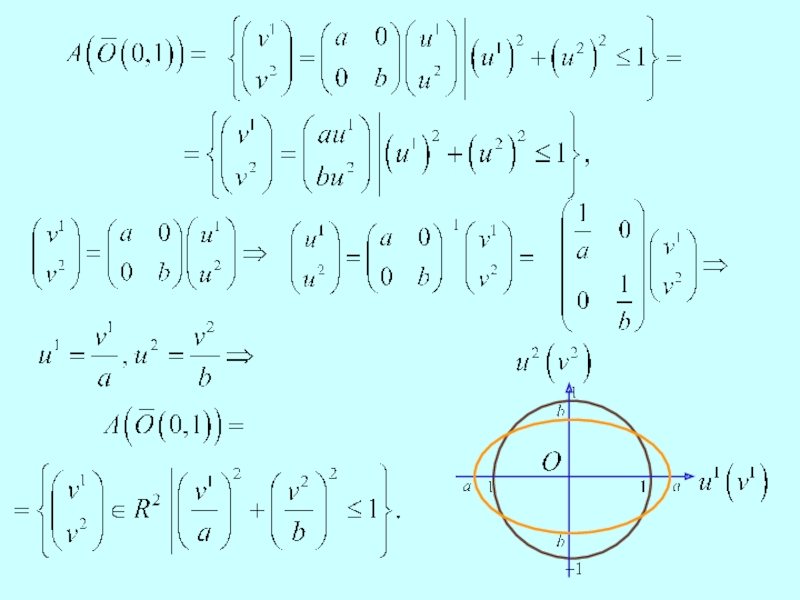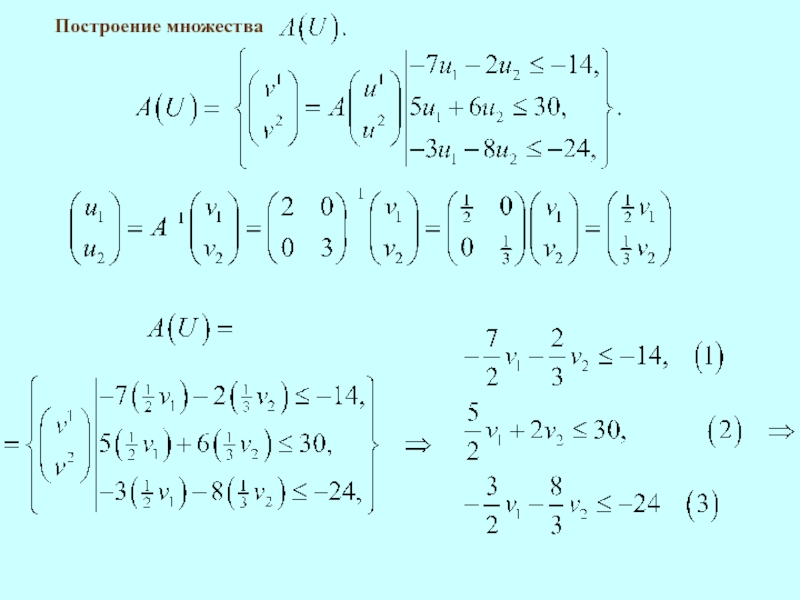- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Выпуклый анализ. Выпуклые множества. Лекция 5 презентация
Содержание
- 1. Выпуклый анализ. Выпуклые множества. Лекция 5
- 2. 2. ВЫПУКЛЫЕ МНОЖЕСТВА (ПРОДОЛЖЕНИЕ) 2.2.
- 3. 2.2. Аффинные множества.
- 6. Определение 4. Дадим
- 7. 2.3. Размерность множества.
- 8. Определение 7.
- 9. 2.4. Операции над выпуклыми
- 10. Тогда
- 11. и формула
- 12. Теорема 8. При
- 14. Упражнение 1. Решение. Убедиться в его выпуклости
Слайд 22. ВЫПУКЛЫЕ МНОЖЕСТВА (ПРОДОЛЖЕНИЕ)
2.2. Аффинные множества.
2.4. Операции над выпуклыми множествами.
2.3. Размерность множества.
Слайд 3
2.2. Аффинные множества.
Определение 2.
справедливо включение
Геометрический смысл данного определения
проходящую через эти точки.
содержит и всю прямую,
Очевидно, что аффинные множества выпуклы.
Теорема 2.
Любой сдвиг аффинного множества является аффинным множеством.
Доказательство.
Теорема доказана.
Слайд 6Определение 4.
Дадим геометрическую иллюстрацию полученных результатов.
Теорема 5.
Доказательство аналогично
Пересечение любого числа аффинных множеств
Слайд 7
2.3. Размерность множества.
Определение 5.
Пересечение всех аффинных множеств,
Определение 6.
и вложено в любое другое аффинное множество,
Слайд 9
2.4. Операции над выпуклыми множествами.
сохраняющих их выпуклость относятся:
взятия линейной алгебраической
и линейного преобразования.
Теорема 6.
Любая линейная комбинация конечного числа выпуклых множеств выпукла.
Доказательство.
операции пересечения,
Слайд 10
Тогда
Теорема доказана.
Теорема 7.
Тогда
Доказательство.
В условиях теоремы докажем обратное
Слайд 12
Теорема 8.
При линейном преобразовании
Доказательство.
Пусть
имеет место включение
Тогда
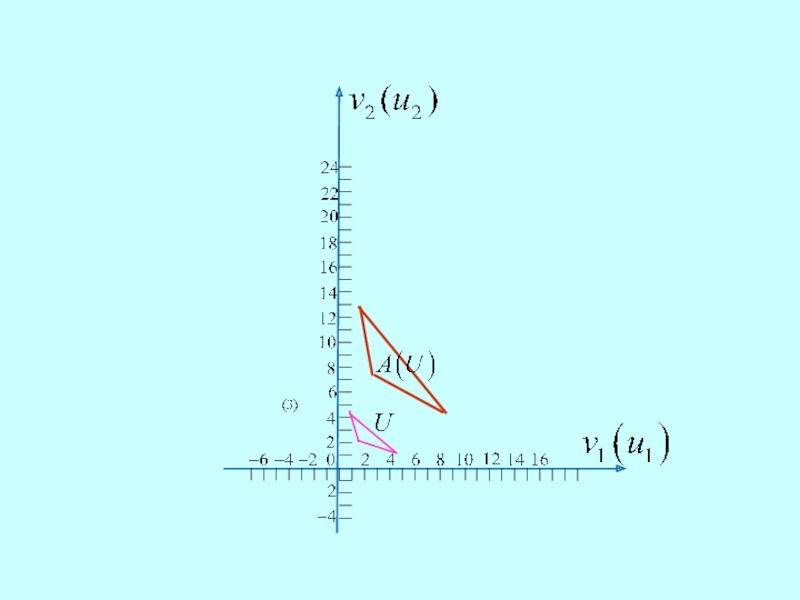
Пример
Пусть
является непустым компактным выпуклым множеством.