- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Гиперкомплексные числа презентация
Содержание
- 1. Гиперкомплексные числа
- 2. Многообразное и успешное применение
- 3. История гиперкомплексного числа
- 4. Сначала изобретение кватернионов и других
- 5. Однако довольно быстро интерес к
- 6. Понятие гиперкомплексного числа Гиперкомплексные
- 7. Итак, назовем гиперкомплексным числом ранга
- 8. Действие сложения определим естественной формулой:
- 9. Сверх того, должно быть
- 10. Операции над гиперкомплексными числами
- 11. В случае кватернионов таблица содержит девять
- 12. Понятно, что каждая клетка заменяет
- 13. Множество всех выражений , в
- 14. Отметим некоторые свойства операции умножения, справедливые в
- 15. Свойства над гиперкомплексными числами 1. Для
- 16.
- 17. Применение гиперкомплексных чисел Применение гиперкомплексных чисел
- 18. Вычисление градиента на основе стандартной матрицы Собела
- 19. рис.2. Изображение, полученное при использовании матриц Собела,
- 20. Нужно учитывать то, что операции вычисления модуля
- 21. Результат действия этих матриц, при использовании второго
- 22. рис.4. Гиперкомплексный градиент, вычисленный при использовании выражения
- 23. Как видно из полученных результатов, вычисленный гиперкомплексный
- 24. На данный момент не совсем понятно, как
Слайд 1Гиперкомплексные числа
Выполнили:
Король Екатерина,
Крылова Кристина,
Лескина Наталья
Панкратова Инесса.
Слайд 2 Многообразное и успешное применение комплексных чисел побудило математиков
Слайд 3История гиперкомплексного числа
В 1843 году ирландский
Слайд 4 Сначала изобретение кватернионов и других гиперкомплексных чисел было воспринято
Слайд 5 Однако довольно быстро интерес к этой тематике спал, потому
Слайд 6Понятие гиперкомплексного числа
Гиперкомплексные числа — конечномерные алгебры над полем
Слайд 7 Итак, назовем гиперкомплексным числом ранга n число, изображающееся совокупностью
a1=b1, a2=b2,…,an=bn.
Слайд 8 Действие сложения определим естественной формулой:
(a1,a2,…,an)+(b1,b2,…,bn)=(a1+b1,a2+b2,…,an+bn),
аналогичной
a(a1,a2,…,an)=(aa1,aa2,…,aan)
Слайд 9 Сверх того, должно быть определено действие умножения двух
Слайд 10Операции над гиперкомплексными числами
Сложение и вычитание определяются формулами, а
Слайд 11 В случае кватернионов таблица содержит девять равенств и может быть
ijk
i-1k-j
j-k-1i
kj-i-1
Слайд 12 Понятно, что каждая клетка заменяет одно из равенств таблицы
Слайд 13 Множество всех выражений , в котором операции сложения и
Слайд 14Отметим некоторые свойства операции умножения, справедливые в любой гиперкомплексной системе:
2) Если и -- гиперкомплексные числа, то, где а и b -- произвольные действительные числа.
3) Справедливы оба варианта (левый и правый) распределительного закона: Свойства 1), 2), 3) очевидным образом следуют из самой процедуры умножения
Слайд 15Свойства над гиперкомплексными числами
1. Для любых двух чисел однозначно определена их
2. Для любых двух чисел однозначно определено их произведение.
3. Существует число нуль со свойством; a+0=a для любого а.
4. Для каждого числа а существует противоположное число х, удовлетворяющее равенству a+x=0
5. Сложение переместительно (коммутативно)
a+b=b+a
Слайд 17Применение гиперкомплексных чисел
Применение гиперкомплексных чисел в обработке цветных изображений
Данное применение связано
Слайд 18Вычисление градиента на основе стандартной матрицы Собела и гиперкомплексных чисел
Как известно,
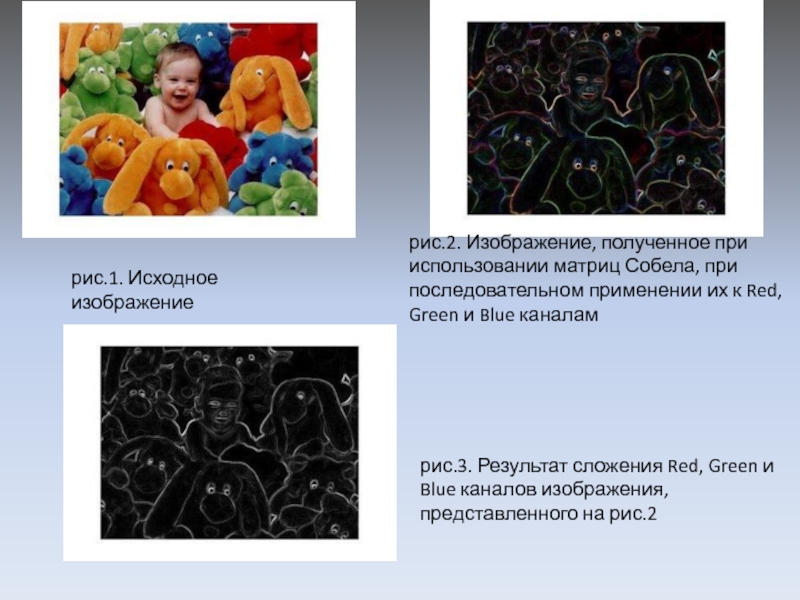
Слайд 19рис.2. Изображение, полученное при использовании матриц Собела, при последовательном применении их
рис.1. Исходное изображение
рис.3. Результат сложения Red, Green и Blue каналов изображения, представленного на рис.2
Слайд 20Нужно учитывать то, что операции вычисления модуля и умножения являются отличными
Слайд 21Результат действия этих матриц, при использовании второго выражения для градиента, дает
Слайд 22рис.4. Гиперкомплексный градиент, вычисленный при использовании выражения для первого модуля гиперкомплексного
рис.5. Гиперкомплексный градиент, вычисленный при использовании выражения для второго модуля гиперкомплексного числа
рис.6. Гиперкомплексный градиент, вычисленный при использовании выражения для третьего модуля гиперкомплексного числа