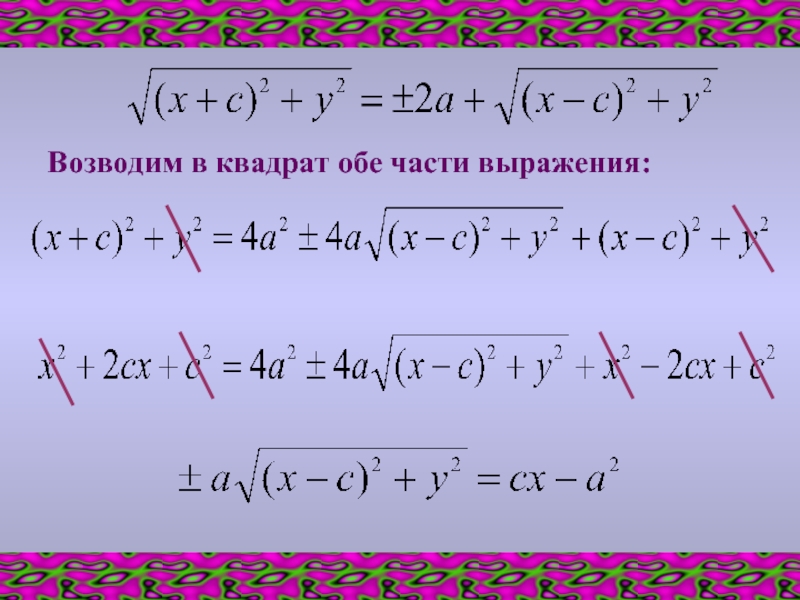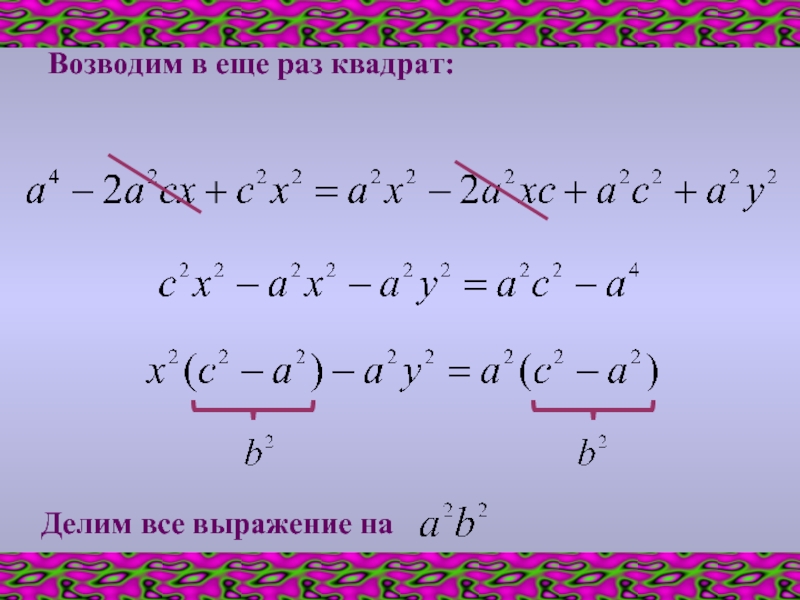каждой из которых
до двух заданных точек, называемых
фокусами, есть величина постоянная
(меньшая, чем расстояние между фокусами)
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Гипербола презентация
Содержание
- 1. Гипербола
- 3. Введем обозначения: a – действительная полуось гиперболы
- 4. Прямые, проходящие через начало координат и имеющие
- 5. ТЕОРЕМА Для того, чтобы точка М(х,у)
- 6. Покажем, что координаты точки, принадлежащей гиперболе, удовлетворяют
- 7. Тогда:
- 8. Возводим в квадрат обе части выражения:
- 9. Возводим в еще раз квадрат: Делим все выражение на
- 10. каноническое уравнение гиперболы
- 11. Отношение фокусного расстояния к длине действительной оси гиперболы называется ЭКСЦЕНТРИСИТЕТОМ
- 12. Для гиперболы Следовательно, для гиперболы Чем
Введем обозначения: a – действительная полуось гиперболы b – мнимая полуось гиперболы Для любой точки М(х,у), принадлежащей гиперболе, по определению выполняется равенство:
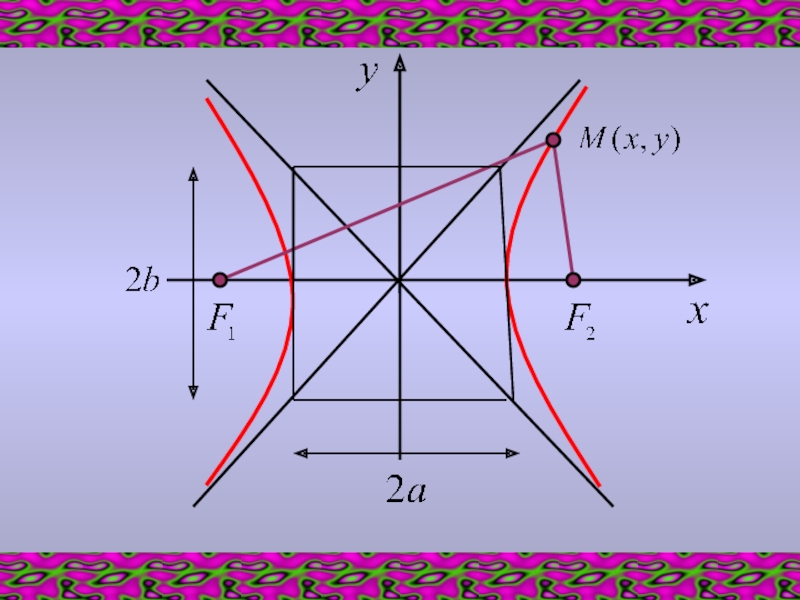
Слайд 14.4. ГИПЕРБОЛА
ГИПЕРБОЛОЙ называется множество
точек плоскости, абсолютная величина
разности расстояний от
Слайд 3Введем обозначения:
a – действительная полуось гиперболы
b – мнимая полуось гиперболы
Для любой
точки М(х,у), принадлежащей гиперболе, по определению выполняется равенство:
Слайд 4Прямые, проходящие через начало координат и имеющие угловые коэффициенты
и
называются асимптотами гиперболы.
Асимптоты
делят плоскость на 4 области, в двух из которых расположена гипербола.
Точки гиперболы по мере удавления от оси у приближаются к асимптотам, т.е. расстояние между точками гиперболы и асимптотой при увеличении х уменьшается и стремится к нулю.
Слайд 5
ТЕОРЕМА
Для того, чтобы точка М(х,у) принадлежала гиперболе, необходимо и достаточно, чтобы
ее координаты удовлетворяли уравнению
где
2
Слайд 6Покажем, что координаты точки, принадлежащей гиперболе, удовлетворяют уравнению (2).
Т.к. точка М(х,у)
принадлежит гиперболе, то по определению гиперболы, должно выполнятся условие
Выразим каждое расстояние по формуле расстояния между двумя точками:
Слайд 11Отношение фокусного расстояния к
длине действительной оси гиперболы
называется
ЭКСЦЕНТРИСИТЕТОМ
Слайд 12Для гиперболы
Следовательно, для гиперболы
Чем меньше отношение мнимой и действительной полуосей,
тем меньше эксцентриситет и тем более гипербола будет прижата к оси х, и наоборот.
