- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Геометрическое решение задачи о расстояниях между точками презентация
Содержание
- 1. Геометрическое решение задачи о расстояниях между точками
- 2. Пал Эрдеш Насколько мало
- 3. Задачи: ? Цель: Найти
- 4. P=1 N=d+1 Каждая грань вписана Р(n)
- 5. Л. Гут Н. Кац У точки есть
- 6. Актуальное решение проблемы. Множества на прямой. а
- 7. Если фигура вписана, она имеет вертикальную ось
- 8. Исследуемый объект- выпуклая фигура по внешнему контуру,
Слайд 1Геометрическое решение задачи о расстояниях между точками
Выполнил Кудряшов Александр, ученик 8
Научный руководитель: Алякин Владимир Алексеевич
Слайд 2
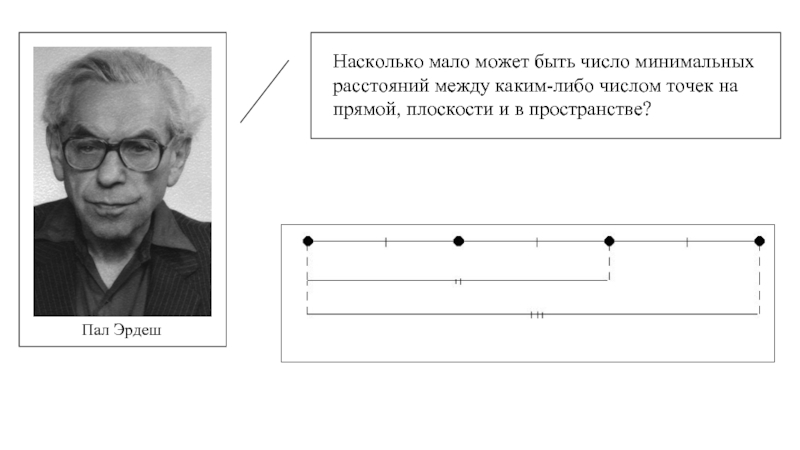
Пал Эрдеш
Насколько мало может быть число минимальных расстояний между каким-либо числом
Слайд 3Задачи:
?
Цель:
Найти ответ на поставленный Эрдешом вопрос
Р – число различных расстояний
n-число
n(1)=n(2)
P(1)=P(2)
Число вариантов?
Функция P(N мал.)=функция Р(n большое) ?
P(n)=?
P(n) (d)?
Слайд 4P=1
N=d+1
Каждая грань вписана
Р(n) зависит в т.ч. от константы с.
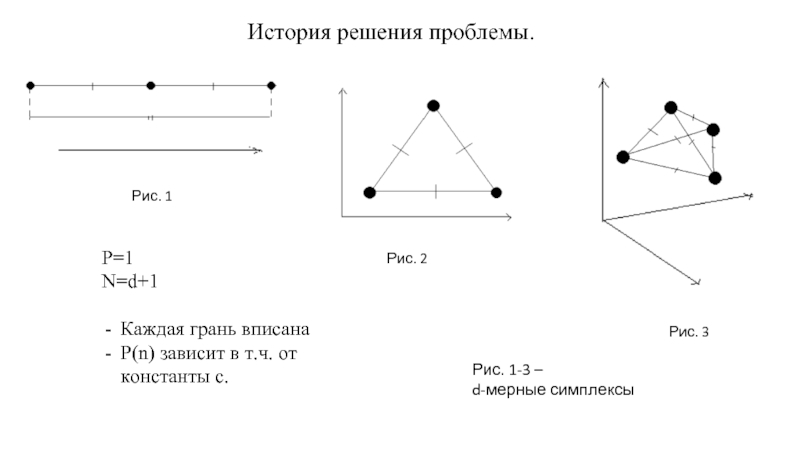
Рис. 1
Рис. 2
Рис.
Рис. 1-3 –
d-мерные симплексы
История решения проблемы.
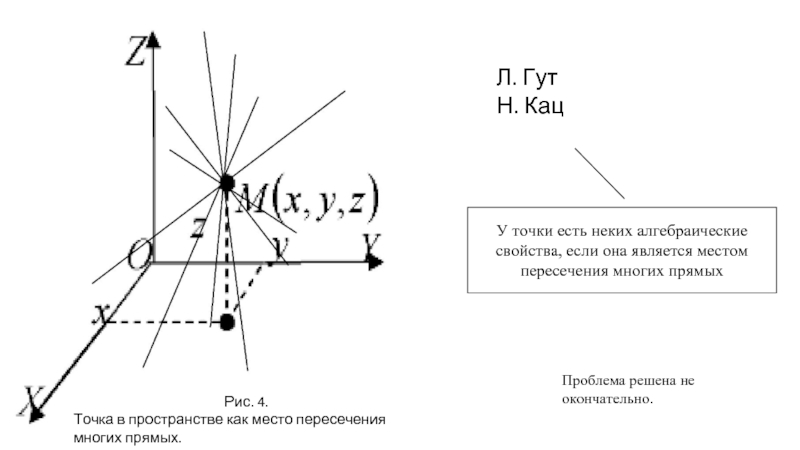
Слайд 5Л. Гут
Н. Кац
У точки есть неких алгебраические свойства, если она является
Рис. 4.
Точка в пространстве как место пересечения многих прямых.
Проблема решена не окончательно.
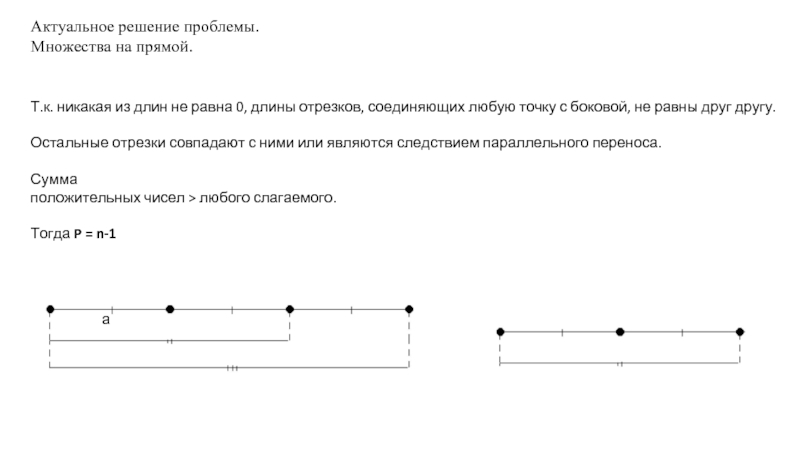
Слайд 6Актуальное решение проблемы.
Множества на прямой.
а
Т.к. никакая из длин не равна 0,
Остальные отрезки совпадают с ними или являются следствием параллельного переноса.
Сумма
положительных чисел > любого слагаемого.
Тогда P = n-1
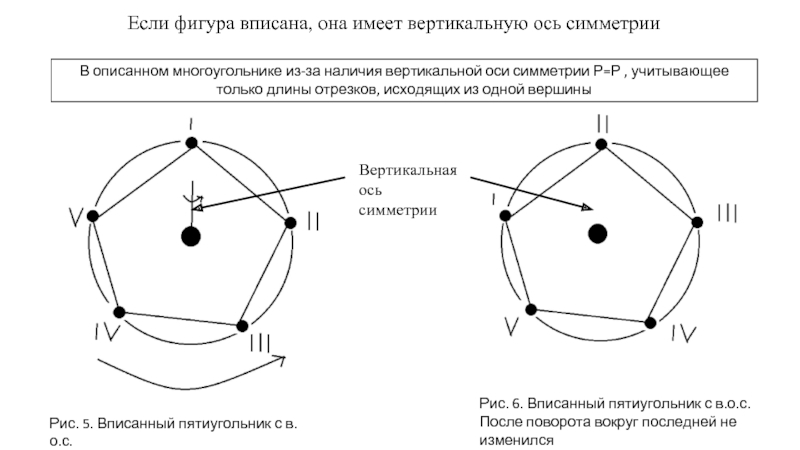
Слайд 7Если фигура вписана, она имеет вертикальную ось симметрии
Рис. 5. Вписанный пятиугольник
Вертикальная
ось
симметрии
Рис. 6. Вписанный пятиугольник с в.о.с.
После поворота вокруг последней не изменился
В описанном многоугольнике из-за наличия вертикальной оси симметрии Р=Р , учитывающее только длины отрезков, исходящих из одной вершины
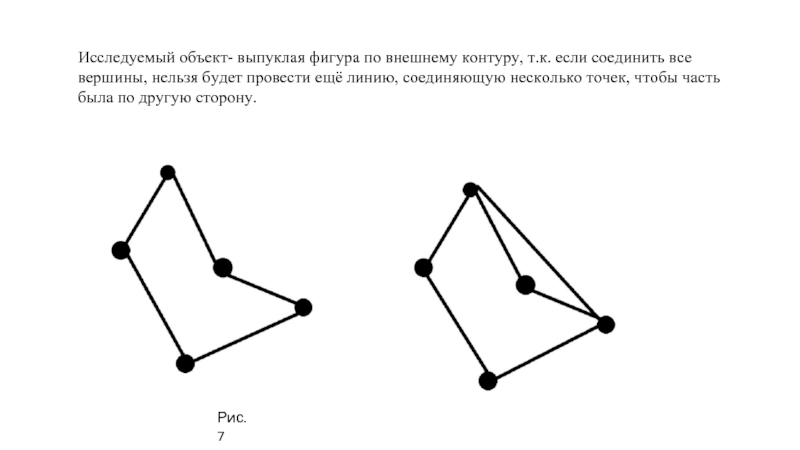
Слайд 8Исследуемый объект- выпуклая фигура по внешнему контуру, т.к. если соединить все
Рис.7