- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Задачи раскраски графов. Вершинная раскраска презентация
Содержание
- 1. Задачи раскраски графов. Вершинная раскраска
- 2. Вершинная раскраска Раскрасить вершины графа в минимальное
- 3. Хроматическое число Минимальное число цветов, необходимое для
- 4. Нижние оценки для хроматического числа χ
- 5. Конструкция Мицельского Для любого k≥2 cуществуют графы
- 6. Конструкция Мицельского Граф Mk+1 строится из Mk
- 7. Конструкция Мицельского Предположим, что это
- 8. Верхние оценки для хроматического числа Граф называется
- 9. Доказательство Индукция по n: при удалении любой
- 10. Оценка χ ≤ Δ+1 достигается для нечетных
- 11. Доказательство Для Δ≤2 утверждение очевидно. Пусть Δ≥3
- 12. Доказательство 1) В любой раскраске графа H
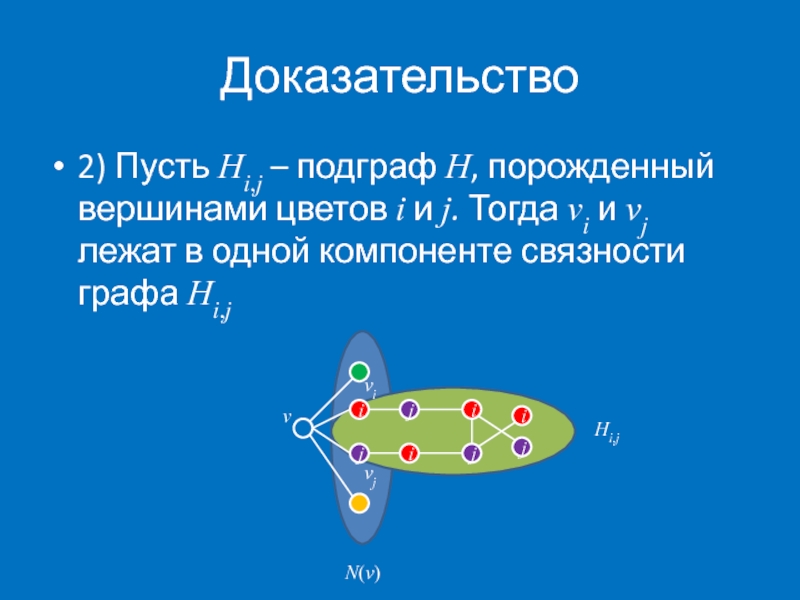
- 13. Доказательство 2) Пусть Hi,j –
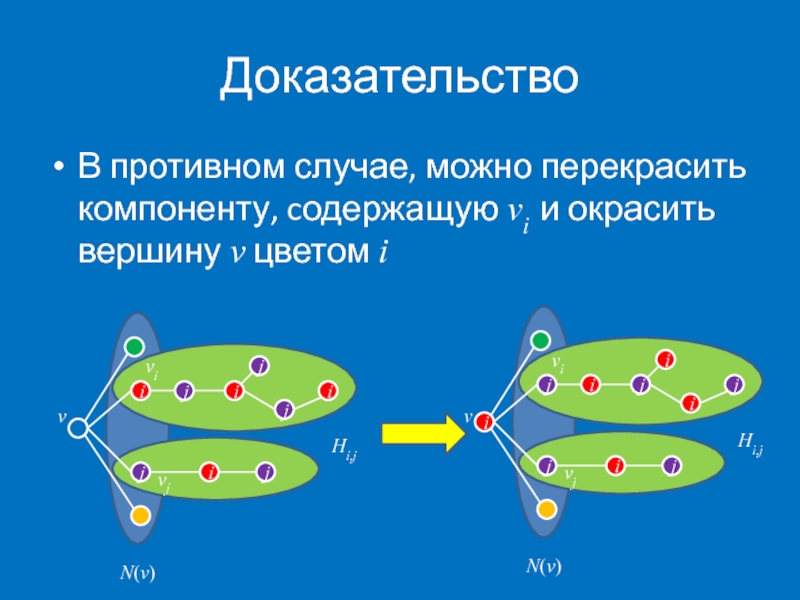
- 14. Доказательство В противном случае,
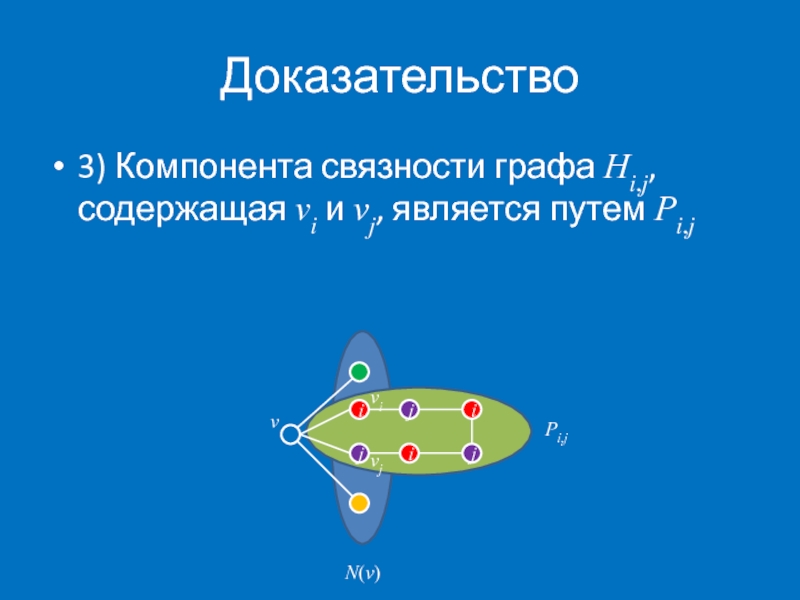
- 15. Доказательство 3) Компонента связности графа
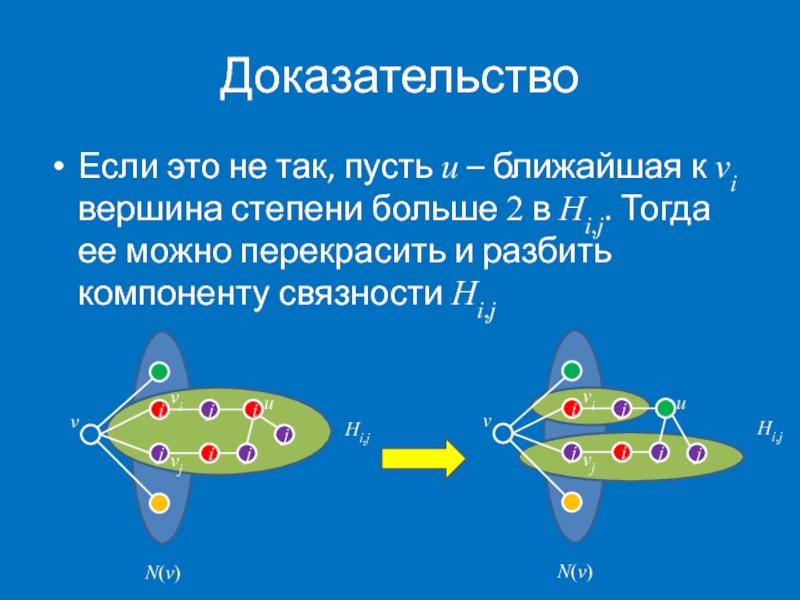
- 16. Доказательство Если это
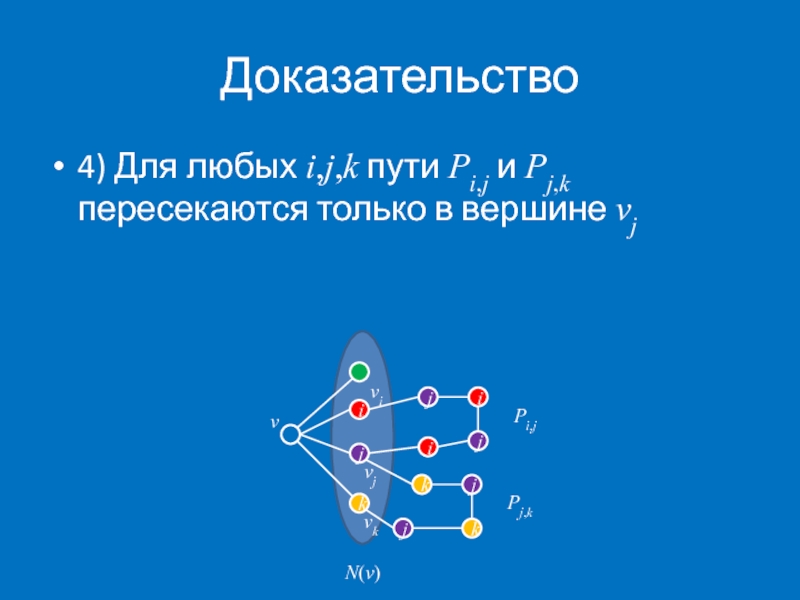
- 17. Доказательство 4) Для любых i,j,k пути
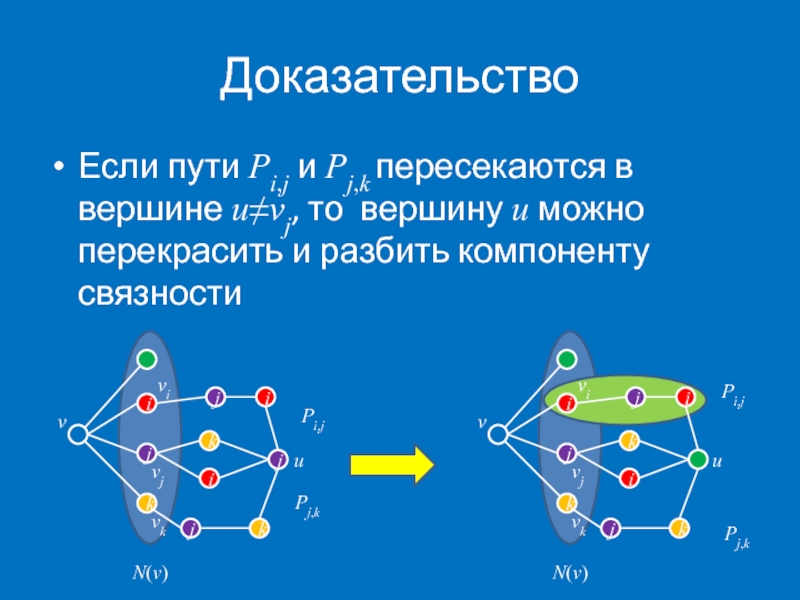
- 18. Доказательство Если пути Pi,j
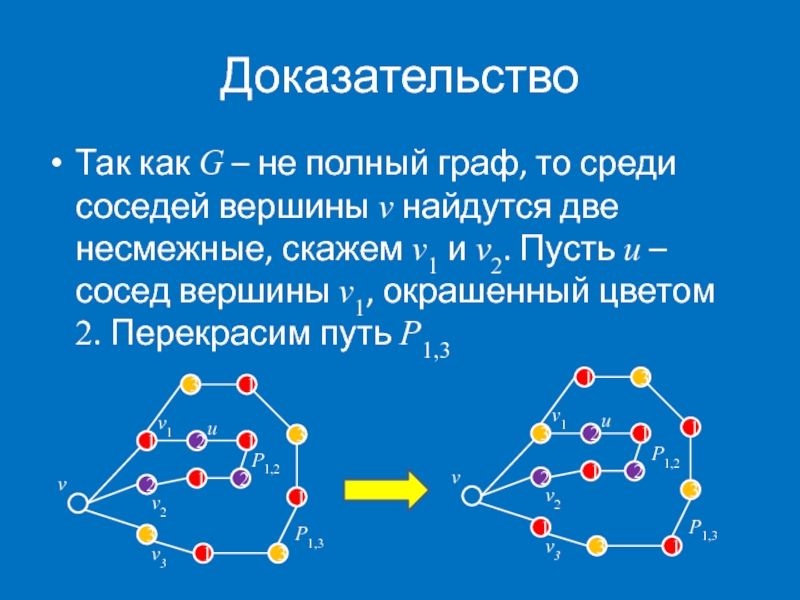
- 19. Доказательство Так как G – не полный
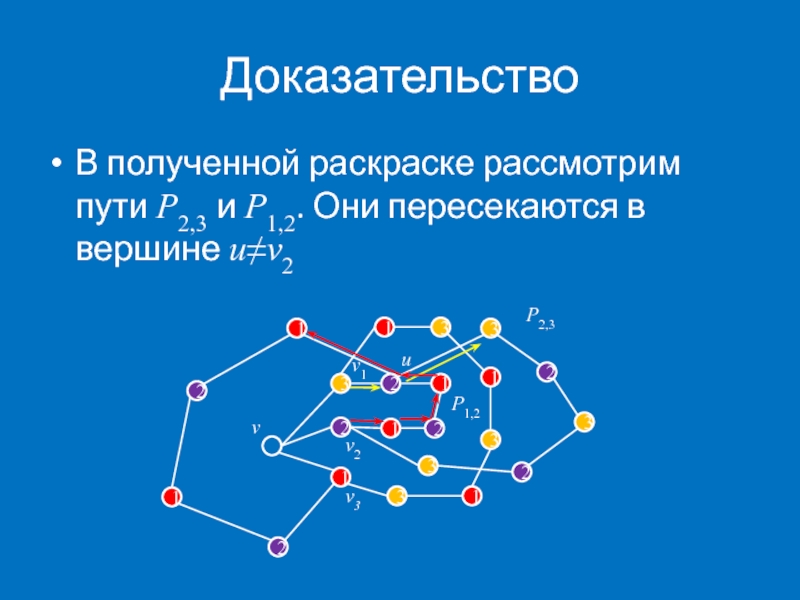
- 20. Доказательство В полученной раскраске рассмотрим пути P2,3
- 21. Реберная раскраска Раскраска ребер в минимальное число
- 22. Очевидно, χ’(G)≥Δ Теорема Кёнига (1916).
- 23. Доказательство Индукция по m Удалим ребро xy
- 24. Доказательство Пусть цвет a свободен при вершине
- 25. Доказательство Эта цепь не может закончиться в
- 26. Верхняя оценка Теорема Визинга (1964). Для любого графа G выполнена оценка χ’(G)≤Δ+1
- 27. Доказательство Индукция по m Для любого ребра
- 28. Доказательство Удалим ребро xy0 и раскрасим полученный
- 29. Доказательство Если при x нет ребра цвета
- 30. Доказательство Значит, найдется такое i, что ak=ai=b.
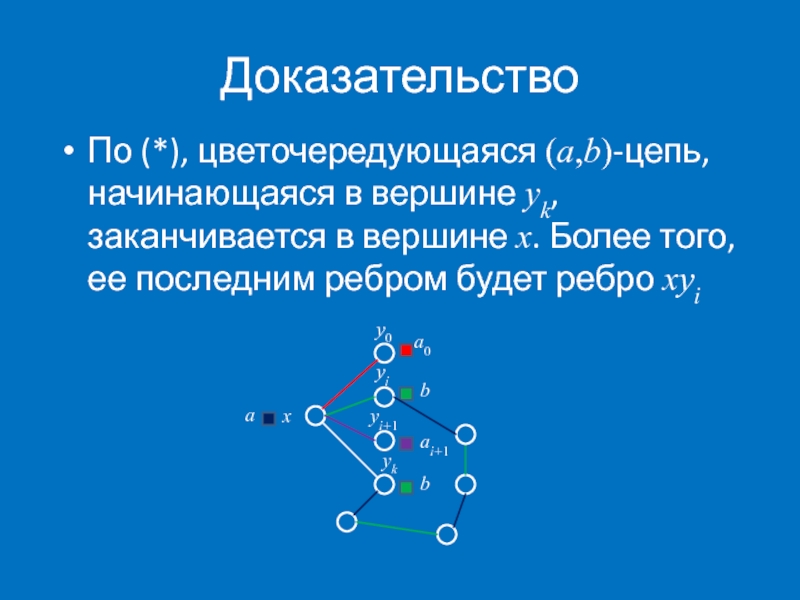
- 31. Доказательство По (*), цветочередующаяся (a,b)-цепь, начинающаяся в
- 32. Доказательство Вернемся к исходной раскраске и перекрасим
- 33. Доказательство Значит, ее можно перекрасить и окрасить
- 34. Предписанная раскраска Каждая вершина (ребро) имеет свой
- 35. Предписанное хроматическое число ch(G) Это минимальное
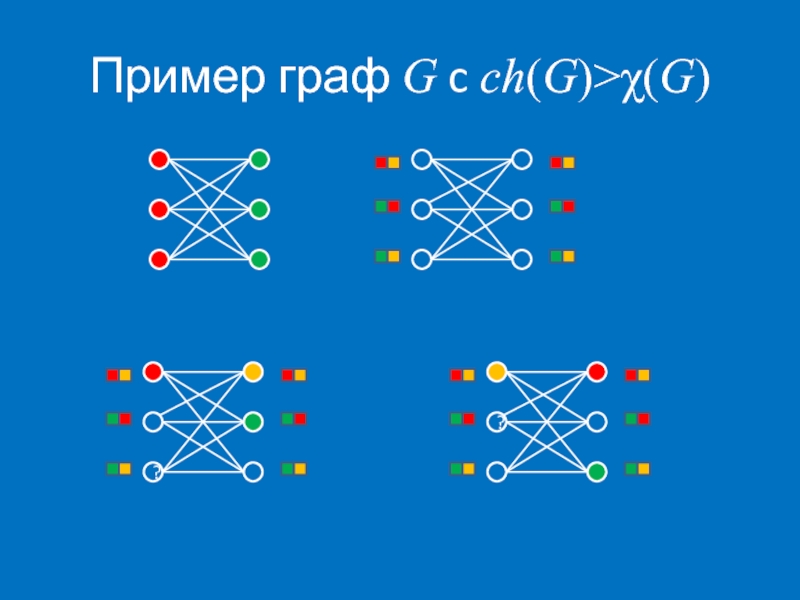
- 36. Пример граф G c ch(G)>χ(G)
- 37. Теорема. Для любого t≥3 существует двудольный граф
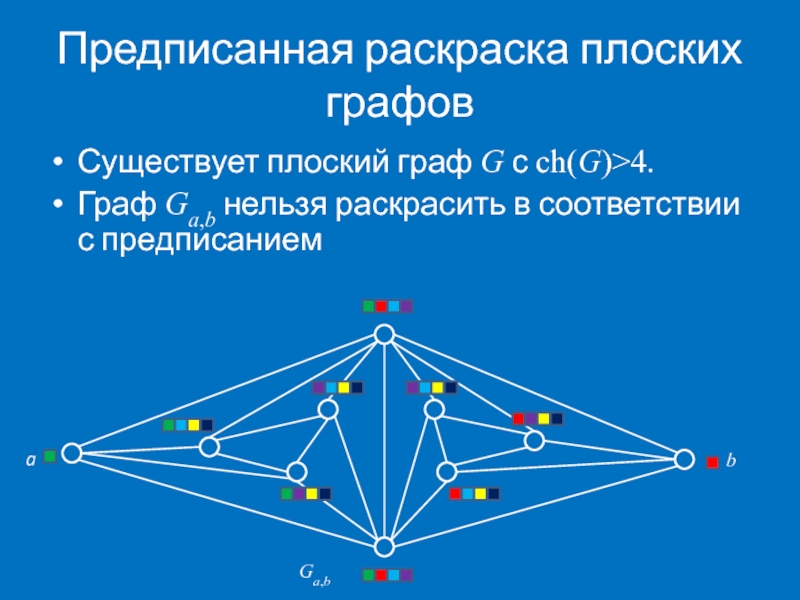
- 38. Предписанная раскраска плоских графов Существует плоский граф
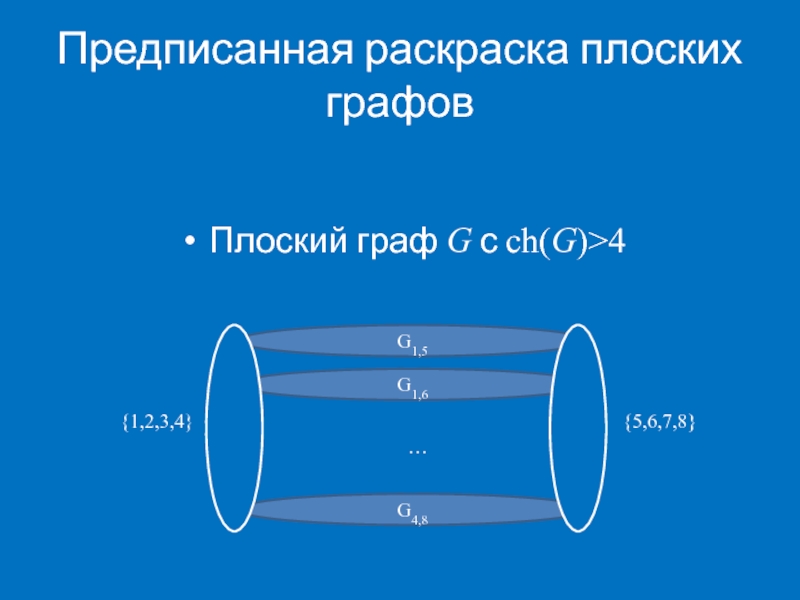
- 40. Предписанная раскраска плоских графов G1,5 G1,6 G4,8
- 41. Предписанная раскраска плоских графов Теорема Томассена (1994). Если G – плоский, то ch(G)≤5
- 42. Предписанная раскраска плоских графов Лемма. Пусть в
- 43. Доказательство Индукция по n. Рассмотрим 2 случая
- 44. Доказательство x C2 v1
- 45. Доказательство Случай 2. В цикле C нет
- 46. Доказательство В предписании вершины vk выберем цвета
- 47. Доказательство По индукции раскрасим граф G’ в
- 48. Предписанная раскраска ребер Гипотеза Визинга. Для
- 49. Лемма. Пусть в графе G задано вершинное
- 50. Доказательство леммы Индукция по n. Выберем цвет
- 51. Доказательство теоремы Рассмотрим граф H=L(G). Построим
- 52. Доказательство теоремы Пусть e1 и e2 –
- 53. Доказательство теоремы Ясно, что |d+(v)|≤Δ−1, так как
- 54. Доказательство теоремы Предположим, условие (2) леммы не
- 55. Доказательство теоремы Пусть X’ – подмножество вершин
- 56. Доказательство теоремы Ясно, что из любой другой
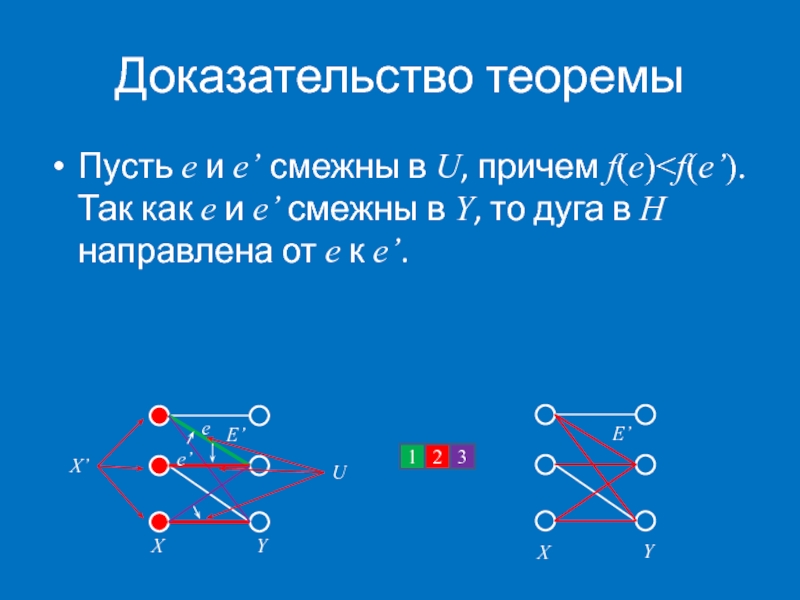
- 57. Доказательство теоремы Пусть e и e’ смежны в U, причем f(e)
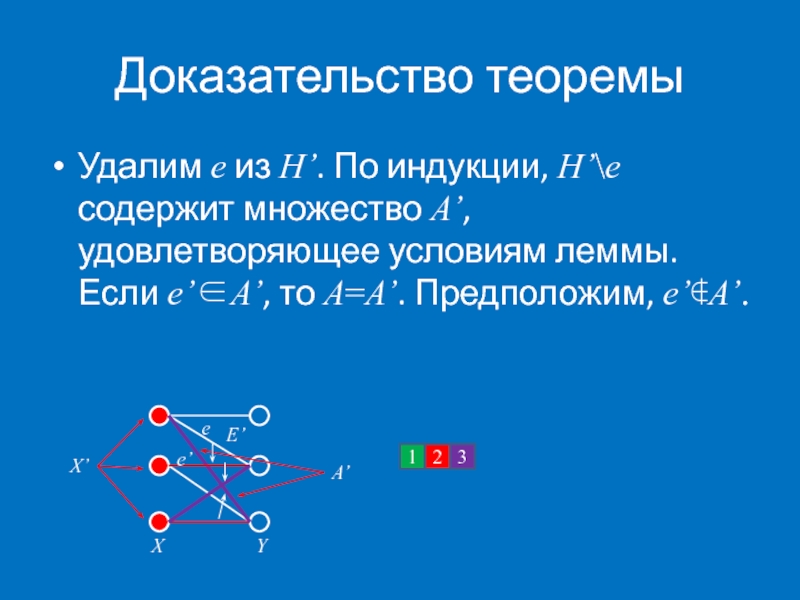
- 58. Доказательство теоремы Удалим e из H’. По
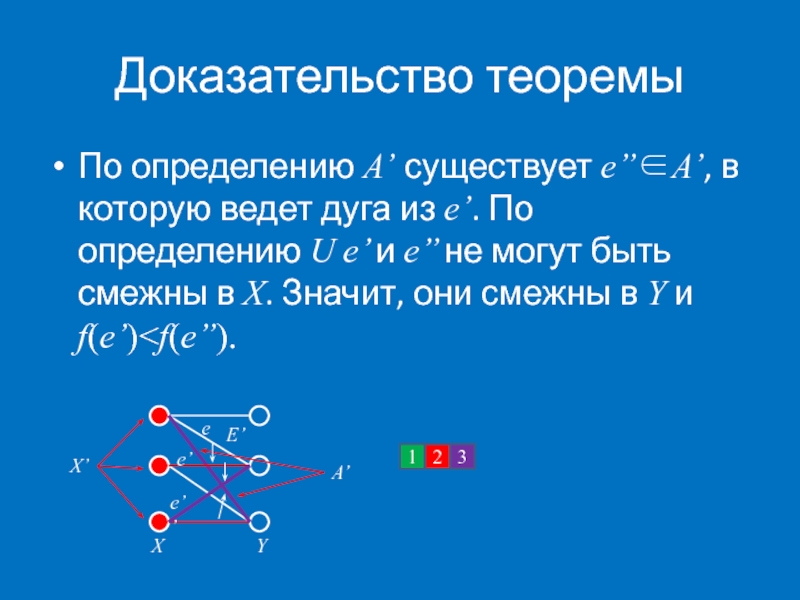
- 59. Доказательство теоремы По определению A’ существует e’’∈A’,
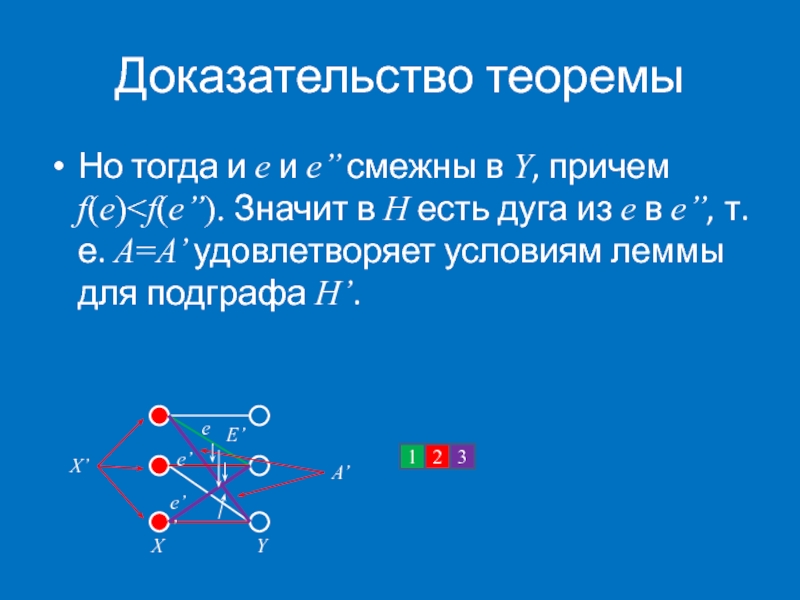
- 60. Доказательство теоремы Но тогда и e и e’’ смежны в Y, причем f(e)
- 61. Упражнения 1. Доказать, что если G’ –
- 62. Спасибо за внимание!
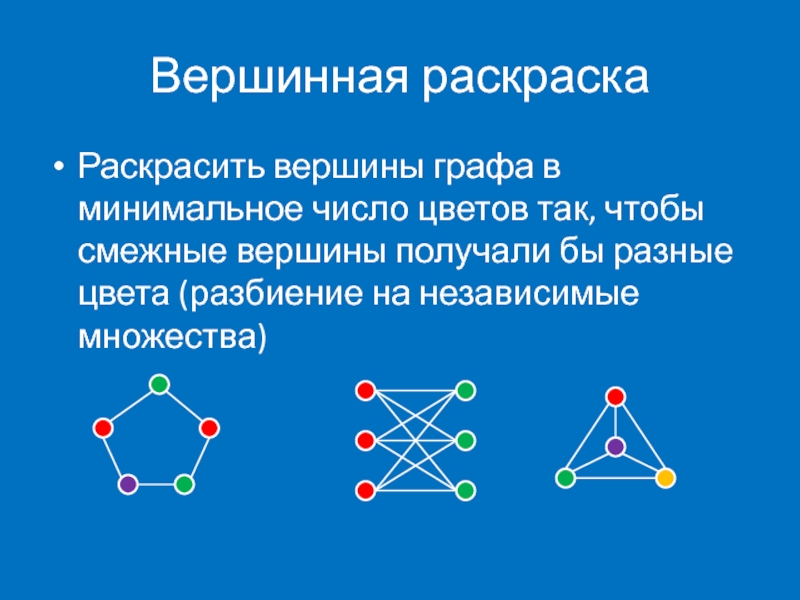
Слайд 2Вершинная раскраска
Раскрасить вершины графа в минимальное число цветов так, чтобы смежные
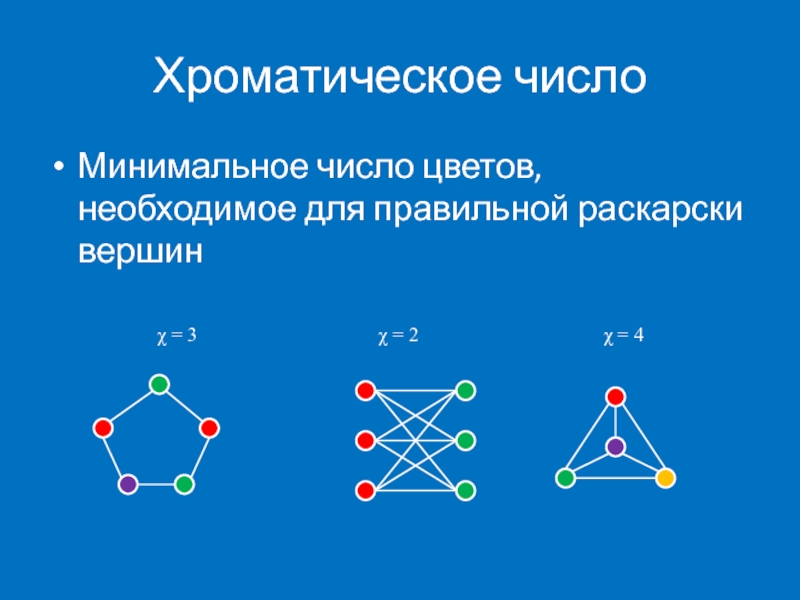
Слайд 3Хроматическое число
Минимальное число цветов, необходимое для правильной раскарски вершин
χ =
χ = 4
χ = 2
Слайд 4Нижние оценки для хроматического числа
χ ≥ ω, где ω – мощность
χ ≥ n/α, где n – число вершин, а α – мощность максимального независимого множества
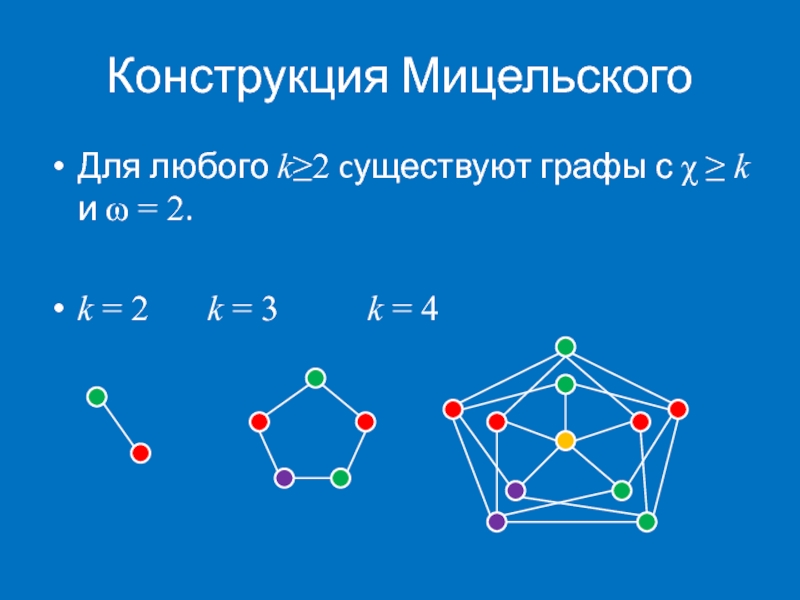
Слайд 6Конструкция Мицельского
Граф Mk+1 строится из Mk следующим образом: для каждой вершины
Покажем, что Mk+1 нельзя раскрасить в k цветов
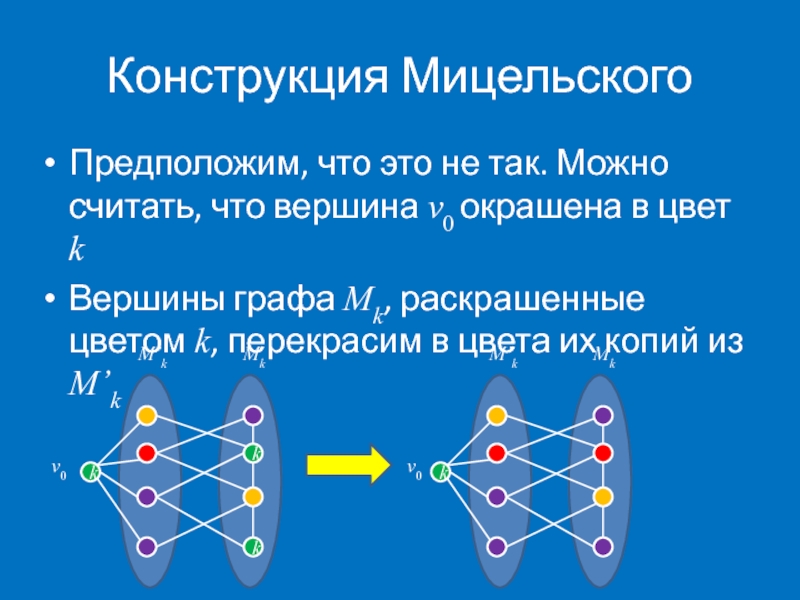
Слайд 7
Конструкция Мицельского
Предположим, что это не так. Можно считать, что вершина v0
Вершины графа Mk, раскрашенные цветом k, перекрасим в цвета их копий из M’k
k
k
k
M’k
Mk
k
M’k
Mk
v0
v0
Слайд 8Верхние оценки для хроматического числа
Граф называется t-вырожденным, если в любом его
Теорема. Если граф t-вырожденный, то
χ ≤ t+1
Слайд 9Доказательство
Индукция по n: при удалении любой вершины граф остается t-вырожденным
Удалим вершину
Красим вершину v в цвет, отсутствующий среди цветов ее соседей
Следствие. χ ≤ Δ+1, где Δ – максимальная степень графа
Слайд 10Оценка χ ≤ Δ+1 достигается для нечетных циклов (Δ=2, χ=3) и
Теорема Брукса (1941). Если граф G не является полным графом или нечетным циклом, то χ(G) ≤ Δ.
Слайд 11Доказательство
Для Δ≤2 утверждение очевидно. Пусть Δ≥3
Индукция по n. Удалим из G
Полученный граф H можно раскрасить в Δ цветов (если H не является полным или нечетным циклом, то по индукции; иначе, степень графа H равна Δ – 1).
Слайд 12Доказательство
1) В любой раскраске графа H все цвета 1,2,…,Δ присутствуют среди
Δ
2
1
N(v)
v1
vΔ
v2
v
Слайд 13
Доказательство
2) Пусть Hi,j – подграф H, порожденный вершинами цветов i и
j
i
N(v)
vj
vi
i
i
j
j
i
j
Hi,j
v
Слайд 14
Доказательство
В противном случае, можно перекрасить компоненту, cодержащую vi и окрасить вершину
j
i
N(v)
vj
vi
i
i
j
j
j
j
i
Hi,j
i
j
j
N(v)
vj
vi
j
i
j
i
i
i
j
Hi,j
v
v
Слайд 15
Доказательство
3) Компонента связности графа Hi,j, содержащая vi и vj, является путем
j
i
N(v)
vj
vi
i
i
j
j
v
Pi,j
Слайд 16
Доказательство
Если это не так, пусть u – ближайшая к vi вершина
j
i
N(v)
vj
vi
i
i
j
j
v
Hi,j
j
j
i
N(v)
vj
vi
i
j
j
v
Hi,j
j
u
u
Слайд 17
Доказательство
4) Для любых i,j,k пути Pi,j и Pj,k пересекаются только в
k
j
i
N(v)
vj
vi
i
i
j
j
v
Pi,j
vk
k
k
j
j
Pj,k
Слайд 18
Доказательство
Если пути Pi,j и Pj,k пересекаются в вершине u≠vj, то вершину
k
j
i
N(v)
vj
vi
i
i
j
j
v
Pi,j
vk
k
k
j
Pj,k
k
j
i
N(v)
vj
vi
i
i
j
v
Pi,j
vk
k
k
j
Pj,k
u
u
Слайд 19Доказательство
Так как G – не полный граф, то среди соседей вершины
3
2
1
v2
v1
1
1
2
2
v
P1,2
v3
3
3
1
1
P1,3
u
3
1
1
2
3
v2
v1
1
1
2
2
v
P1,2
v3
1
1
3
3
P1,3
u
1
3
Слайд 20Доказательство
В полученной раскраске рассмотрим пути P2,3 и P1,2. Они пересекаются в
1
2
3
v2
v1
1
1
2
2
v
P1,2
v3
1
1
3
3
P2,3
u
1
3
3
3
3
2
2
1
1
2
2
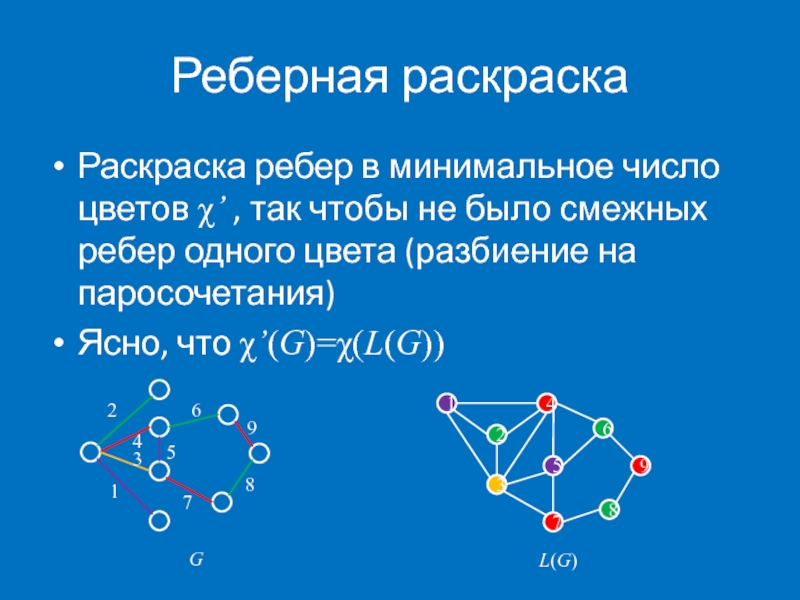
Слайд 21Реберная раскраска
Раскраска ребер в минимальное число цветов χ’ , так чтобы
Ясно, что χ’(G)=χ(L(G))
2
4
1
5
6
8
7
3
9
1
3
4
2
6
5
7
8
9
G
L(G)
Слайд 23Доказательство
Индукция по m
Удалим ребро xy и раскрасим ребра оставшегося графа в
При каждой из вершин x и y останется по крайней мере по одному цвету, не использованному для раскраски примыкающих к ней ребер (свободные цвета).
Слайд 24Доказательство
Пусть цвет a свободен при вершине x. Если он свободен и
Иначе, обозначим через b свободный цвет при вершине y.
Рассмотрим цветочередующуюся (a,b)-цепь, начинающуюся в вершине y.
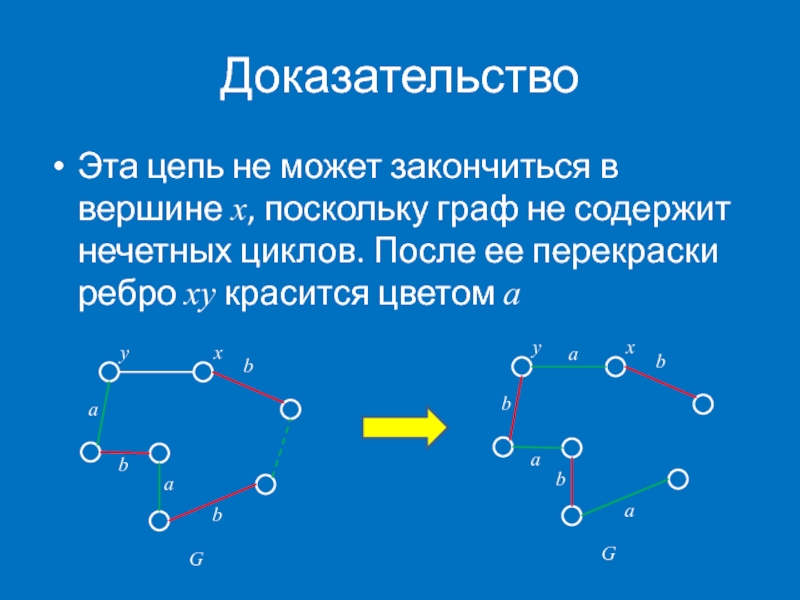
Слайд 25Доказательство
Эта цепь не может закончиться в вершине x, поскольку граф не
y
G
x
a
a
b
b
b
y
G
x
b
a
b
b
a
a
Слайд 27Доказательство
Индукция по m
Для любого ребра xy, граф G\xy красится в Δ+1
(*) Для любых цветов a и b, свободных при вершинах x и y соответственно, цветочередующаяся (a,b)-цепь, начинающаяся в вершине y, заканчивается в вершине x (иначе действуем как в Теореме Кёнига).
Слайд 28Доказательство
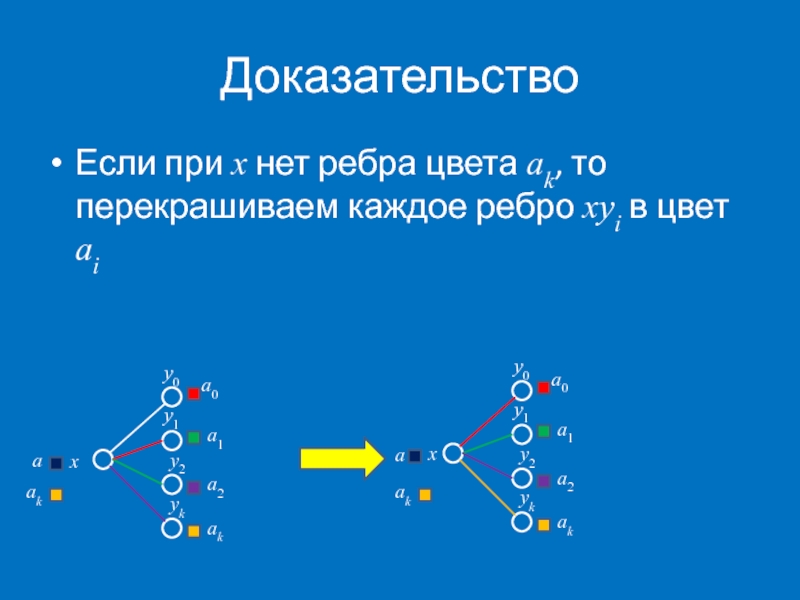
Удалим ребро xy0 и раскрасим полученный граф в Δ+1 цвет. Выберем
Слайд 29Доказательство
Если при x нет ребра цвета ak, то перекрашиваем каждое ребро
y0
y1
a0
a1
y2
yk
a2
ak
y0
y1
a0
a1
y2
yk
a2
ak
x
a
x
a
ak
ak
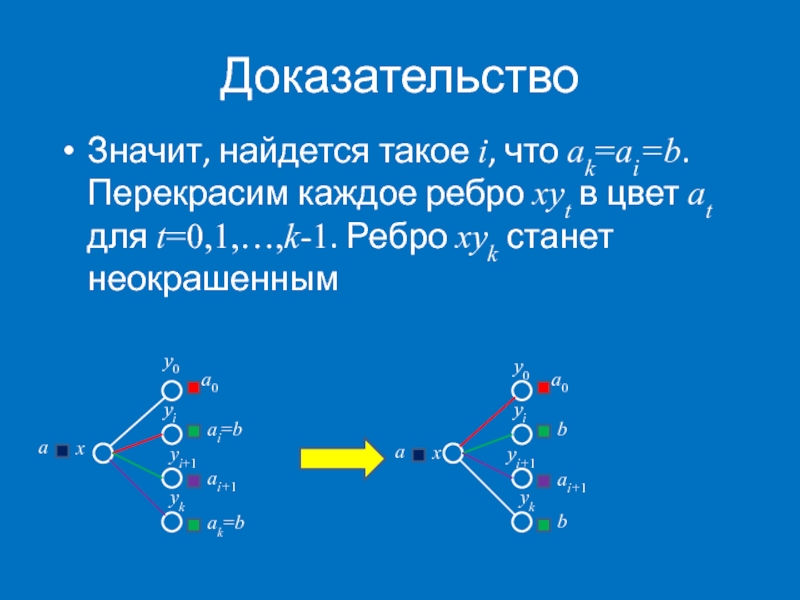
Слайд 30Доказательство
Значит, найдется такое i, что ak=ai=b. Перекрасим каждое ребро xyt в
y0
yi
a0
ai=b
yi+1
yk
ai+1
y0
yi
a0
b
yk
b
yi+1
ai+1
x
a
x
a
ak=b
Слайд 31Доказательство
По (*), цветочередующаяся (a,b)-цепь, начинающаяся в вершине yk, заканчивается в вершине
x
y0
yi
a0
b
yk
b
yi+1
ai+1
a
Слайд 32Доказательство
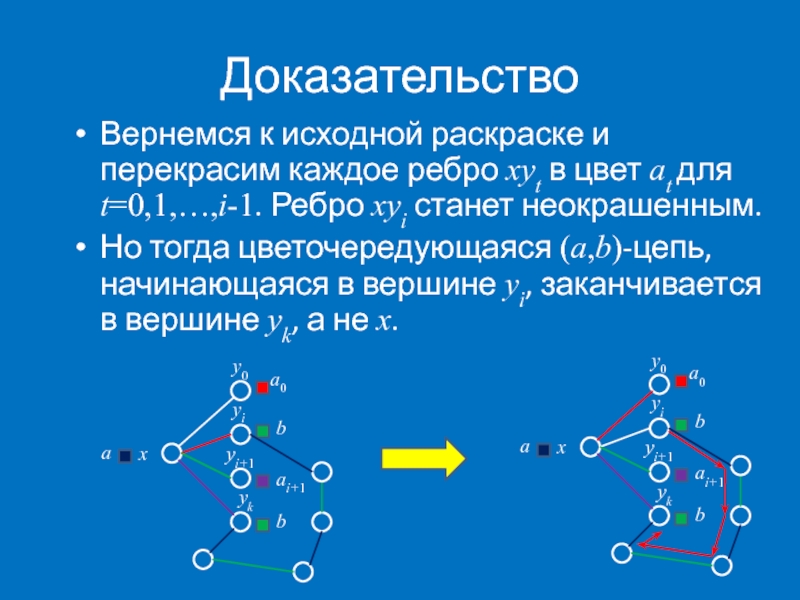
Вернемся к исходной раскраске и перекрасим каждое ребро xyt в цвет
Но тогда цветочередующаяся (a,b)-цепь, начинающаяся в вершине yi, заканчивается в вершине yk, а не x.
x
y0
yi
a0
b
yk
b
yi+1
ai+1
a
x
y0
yi
a0
b
yk
b
yi+1
ai+1
a
Слайд 33Доказательство
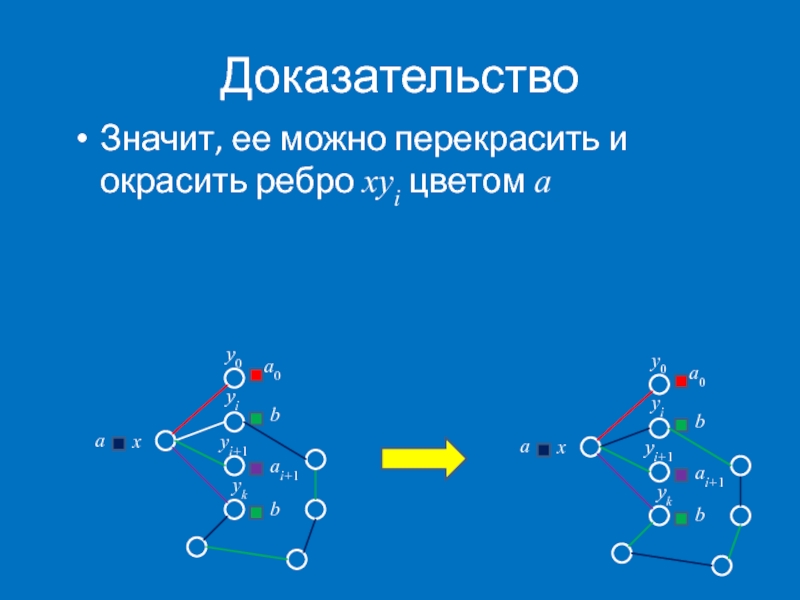
Значит, ее можно перекрасить и окрасить ребро xyi цветом a
x
y0
yi
a0
b
yk
b
yi+1
ai+1
a
x
y0
yi
a0
b
yk
b
yi+1
ai+1
a
Слайд 34Предписанная раскраска
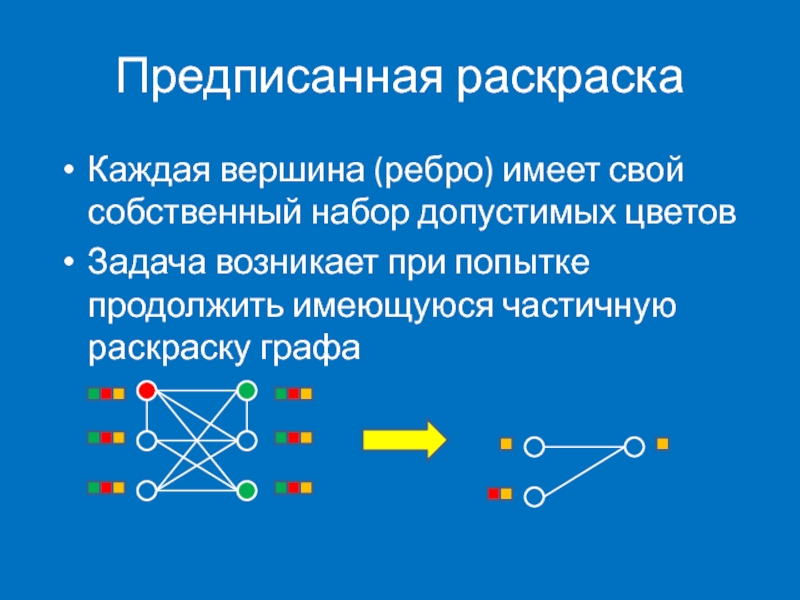
Каждая вершина (ребро) имеет свой собственный набор допустимых цветов
Задача возникает
Слайд 35Предписанное хроматическое число ch(G)
Это минимальное k, при котором граф допускает правильную
Ясно, что ch(G)≥χ(G)
Слайд 37Теорема. Для любого t≥3 существует двудольный граф G с ch(G)>t.
Доказательство. G=Kt,tt
Предписания
Предписания большей доли: все варианты выбора по одному элементу из A1,A2,…,At
Слайд 38Предписанная раскраска плоских графов
Существует плоский граф G с ch(G)>4.
Граф Ga,b нельзя
b
a
Ga,b
Слайд 40Предписанная раскраска плоских графов
G1,5
G1,6
G4,8
{1,2,3,4}
{5,6,7,8}
…
Плоский граф G с ch(G)>4
Слайд 42Предписанная раскраска плоских графов
Лемма. Пусть в плоском графе G внешняя грань
Слайд 43Доказательство
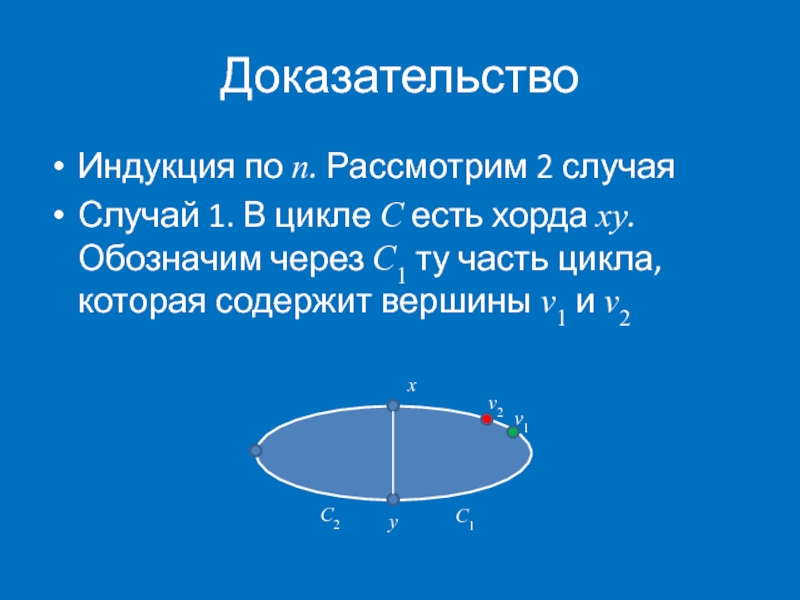
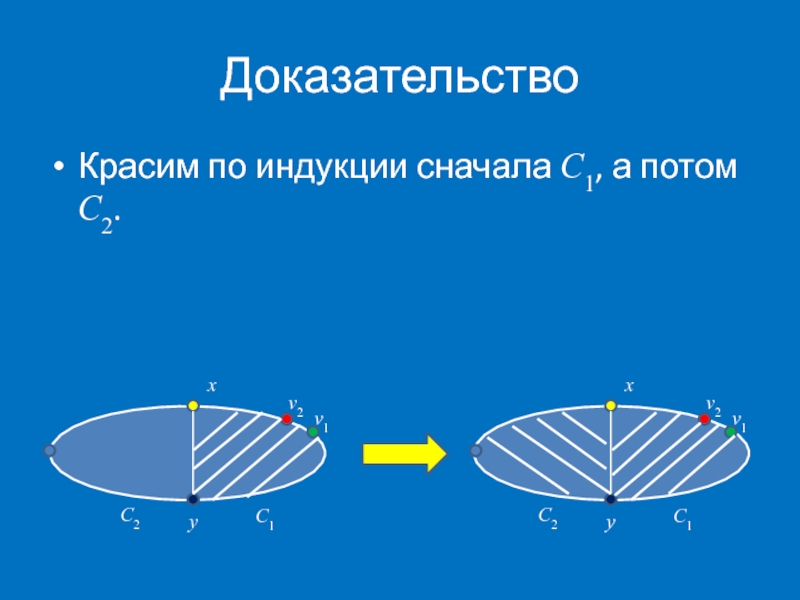
Индукция по n. Рассмотрим 2 случая
Случай 1. В цикле C есть
x
C2
v1
v2
y
C1
Слайд 45Доказательство
Случай 2. В цикле C нет хорд. Обозначим через u1,u2,…,us соседей
u1
u2
v1
v2
C
vk
vk-1
us
Слайд 46Доказательство
В предписании вершины vk выберем цвета c и d, отличные от
u1
u2
v1
v2
C
vk
vk-1
us
a
b
c
d
G’
Слайд 47Доказательство
По индукции раскрасим граф G’ в соответствии с предписанием. Цвета c
u1
u2
v1
v2
C
vk
vk-1
us
a
b
c
d
G’
Слайд 48Предписанная раскраска ребер
Гипотеза Визинга. Для любого графа G, ch’(G)=χ’(G).
Теорема Галвина (1995).
Слайд 49Лемма. Пусть в графе G задано вершинное предписание L. Предположим, ребра
(1) |L(v)|>d+(v) для каждой вершины v
(2) В любом подграфе G’ найдется такое независимое множество A, что из каждой вершины v∈G’\A в A ведет хотя бы одна дуга.
Тогда вершины графа G можно раскрасить в соответствии с предписанием.
Слайд 50Доказательство леммы
Индукция по n.
Выберем цвет a и рассмотрим подграф G’, порожденный
Слайд 51Доказательство теоремы
Рассмотрим граф H=L(G). Построим для него ориентацию, удовлетворяющую условиям леммы.
Пусть
Слайд 52Доказательство теоремы
Пусть e1 и e2 – два смежных в G ребра,
1
3
2
X
Y
Слайд 53Доказательство теоремы
Ясно, что |d+(v)|≤Δ−1, так как у дуги цвета k есть
1
3
2
X
Y
Слайд 54Доказательство теоремы
Предположим, условие (2) леммы не выполнено. Рассмотрим минимальный по числу
X
Y
E’
Слайд 55Доказательство теоремы
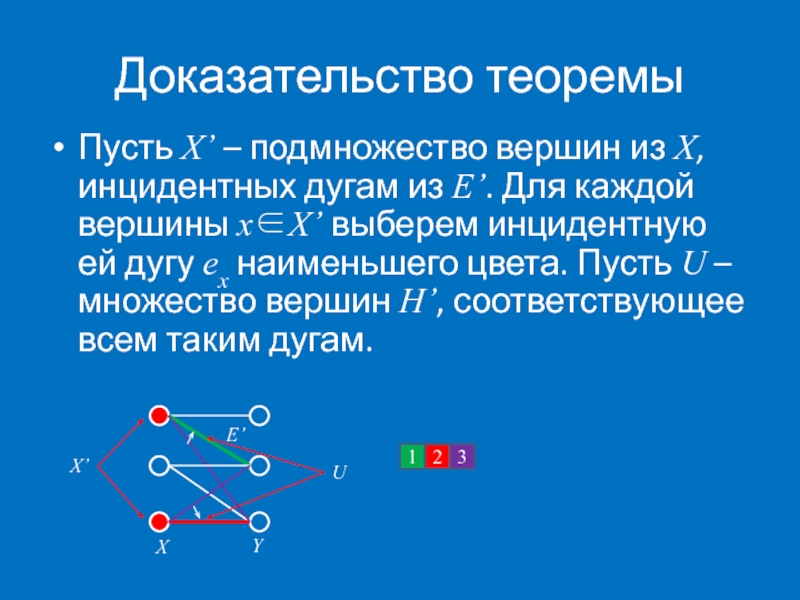
Пусть X’ – подмножество вершин из X, инцидентных дугам из
X
Y
E’
X’
1
3
2
U
Слайд 56Доказательство теоремы
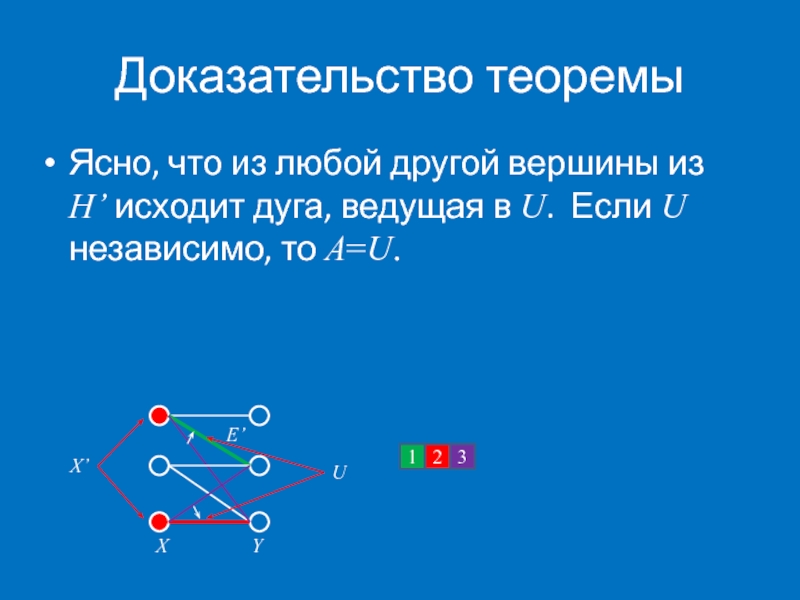
Ясно, что из любой другой вершины из H’ исходит дуга,
X
Y
E’
X’
1
3
2
U
Слайд 57Доказательство теоремы
Пусть e и e’ смежны в U, причем f(e)
X
E’
X’
1
3
2
U
e
e’
Y
X
Y
E’
Слайд 58Доказательство теоремы
Удалим e из H’. По индукции, H’\e содержит множество A’,
X
E’
X’
1
3
2
A’
e
e’
Y
Слайд 59Доказательство теоремы
По определению A’ существует e’’∈A’, в которую ведет дуга из
X
E’
X’
1
3
2
A’
e
e’
Y
e’’
Слайд 61Упражнения
1. Доказать, что если G’ – это дополнение G, то max{χ(G),χ(G’)}≥n1/2
2.
χ(G)≤ 1/2 + (2m+1/4)1/2,
где m – число ребер в G