- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Комплексный чертеж плоскости. Принадлежность точки и прямой плоскости. Взаимное расположение прямой и плоскости презентация
Содержание
- 1. Комплексный чертеж плоскости. Принадлежность точки и прямой плоскости. Взаимное расположение прямой и плоскости
- 2. Комплексный чертеж плоскости Плоскостью общего положения называется
- 3. Следами плоскости называются линии пересечения плоскости с плоскостью проекций (нулевые линии уровня). Σ⊥П1 Σ‖П1 Σ⊥П3
- 4. Плоскости частного положения Плоскости уровня – плоскости
- 5. ∑(ABC)‖П3 A3B3C3-натуральная величина Профильная плоскость уровня Если
- 6. Проецирующие плоскости – плоскости перпендикулярные плоскости проекции.
- 7. Σ(ABC)⊥П3 Профильно - проецирующая плоскость α –
- 8. Принадлежность точки прямой Если точка
- 9. Принадлежность прямой плоскости Прямая принадлежит плоскости, если
- 10. Принадлежность точки плоскости Точка принадлежит плоскости, если
- 11. Параллельность прямой и плоскости Прямая параллельна плоскости,
- 12. Параллельность плоскостей Две плоскости параллельны, если две
- 13. Пересечение прямой с плоскостью 1. Пересечение плоскости
- 14. 2. Пересечение прямой проецирующей с плоскостью Определить
- 15. Определение линии пересечения двух плоскостей, одна из которых проецирующая Σ⊥П1 KM=Σ ∩ Ω(ABC)
- 16. 4. Определение точки пересечения прямой и плоскости
- 18. 5. Определение линии пересечения двух плоскостей Заключить
- 19. 4. Заключить прямую b в плоскость Ψ⊥П1
- 20. 6. Определение линии пересечения двух плоскостей методом
- 21. Перпендикулярность прямой и плоскости Прямая перпендикулярна
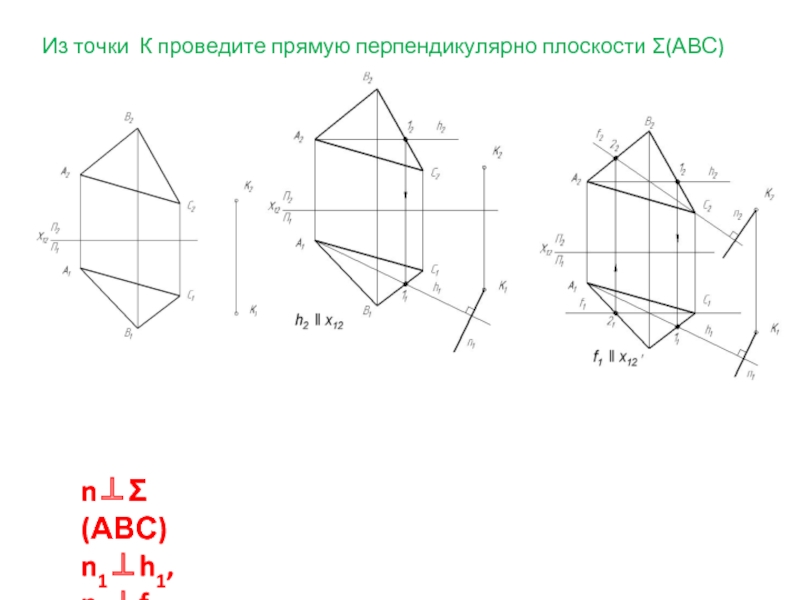
- 22. Из точки К проведите прямую перпендикулярно плоскости Σ(АВС) n⊥Σ(АВС) n1⊥h1, n2⊥f2
- 23. 3. Перпендикулярность двух плоскостей Две плоскости перпендикулярны,
- 24. 4. Перпендикулярность прямых Две прямые перпендикулярны, если
Слайд 1ЛЕКЦИЯ № 2
Комплексный чертеж плоскости
Принадлежность точки и прямой плоскости
Взаимное расположение прямой
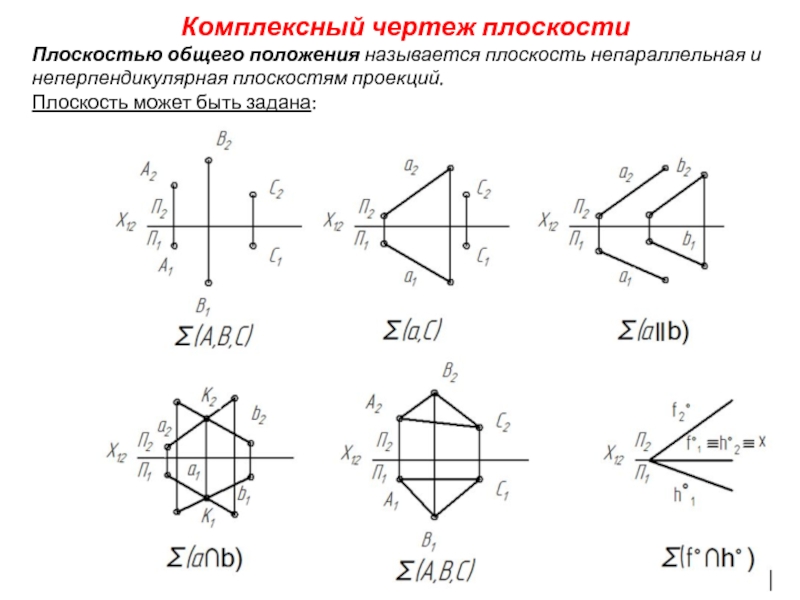
Слайд 2Комплексный чертеж плоскости
Плоскостью общего положения называется плоскость непараллельная и неперпендикулярная плоскостям
Плоскость может быть задана:
Слайд 3Следами плоскости называются линии пересечения плоскости с плоскостью проекций (нулевые линии
Σ⊥П1
Σ‖П1
Σ⊥П3
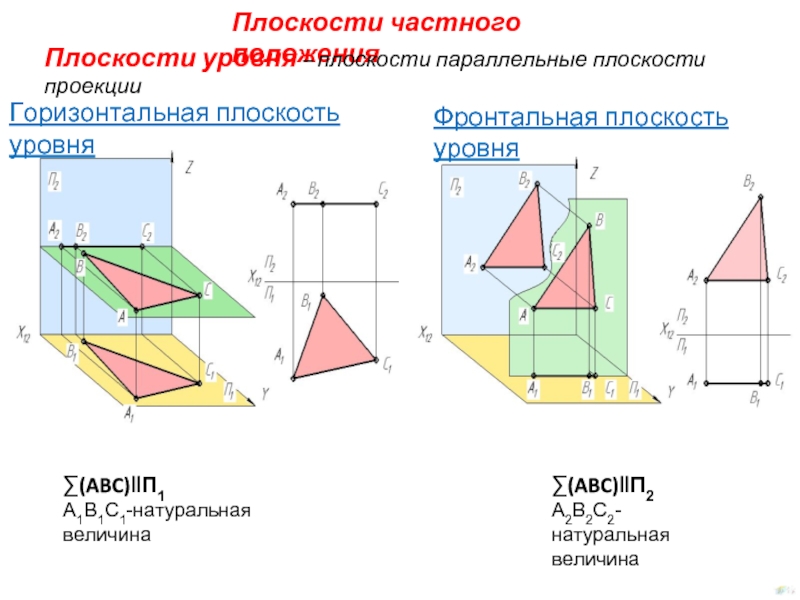
Слайд 4Плоскости частного положения
Плоскости уровня – плоскости параллельные плоскости проекции
∑(ABC)‖П1
A1B1C1-натуральная
величина
Горизонтальная плоскость
∑(ABC)‖П2
A2B2C2-натуральная
величина
Фронтальная плоскость уровня
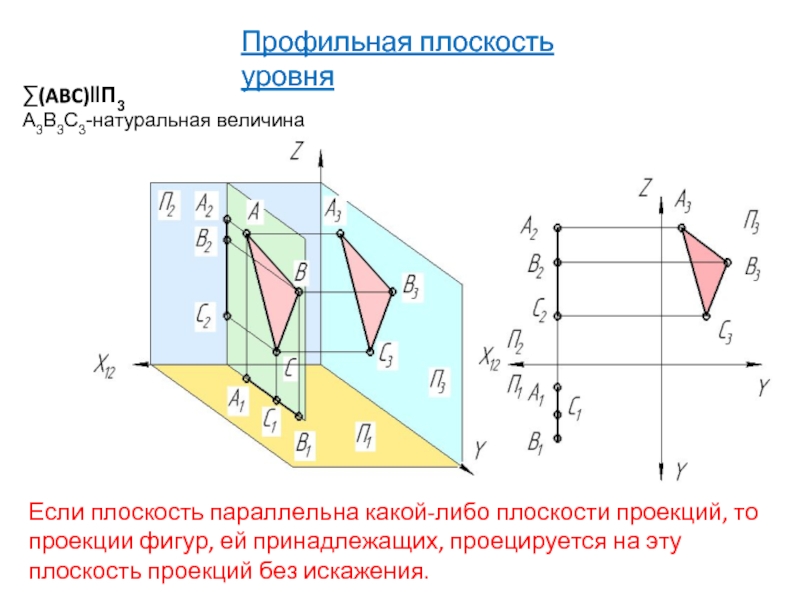
Слайд 5∑(ABC)‖П3
A3B3C3-натуральная величина
Профильная плоскость уровня
Если плоскость параллельна какой-либо плоскости проекций, то проекции
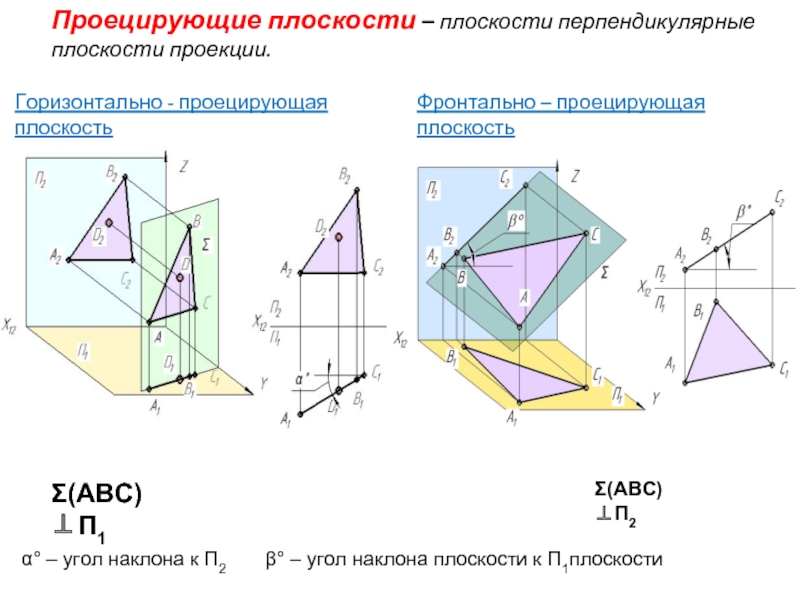
Слайд 6Проецирующие плоскости – плоскости перпендикулярные плоскости проекции.
Σ(ABC)⊥П1
Σ(ABC)⊥П2
α° – угол наклона к
Горизонтально - проецирующая плоскость
Фронтально – проецирующая плоскость
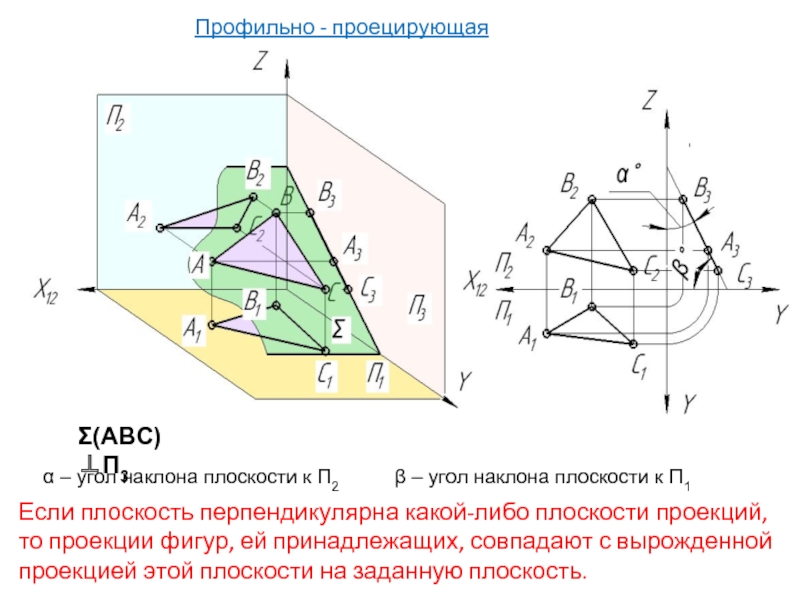
Слайд 7Σ(ABC)⊥П3
Профильно - проецирующая плоскость
α – угол наклона плоскости к П2
Если плоскость перпендикулярна какой-либо плоскости проекций, то проекции фигур, ей принадлежащих, совпадают с вырожденной проекцией этой плоскости на заданную плоскость.
Слайд 8
Принадлежность точки прямой
Если точка принадлежит прямой, то ее проекции принадлежат одноименным
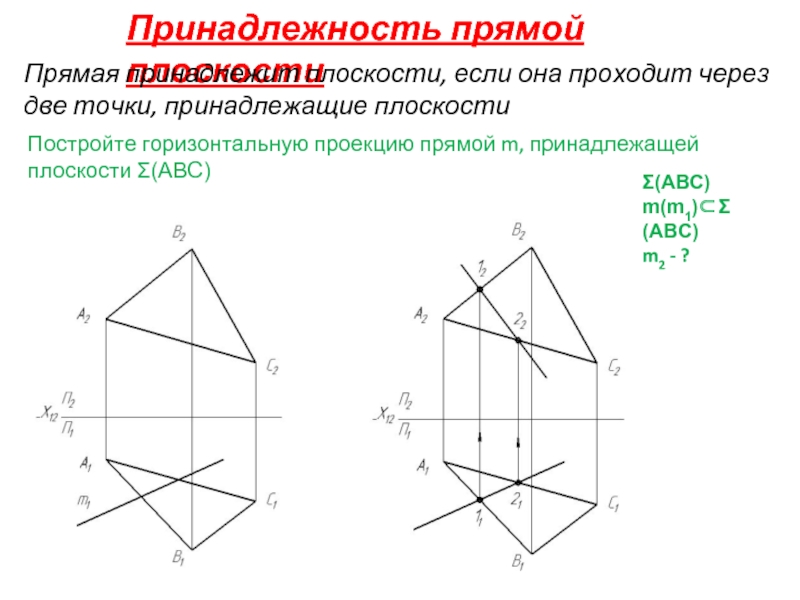
Слайд 9Принадлежность прямой плоскости
Прямая принадлежит плоскости, если она проходит через две точки,
Постройте горизонтальную проекцию прямой m, принадлежащей плоскости Σ(АВС)
Σ(АВС)
m(m1)⊂Σ(АВС)
m2 - ?
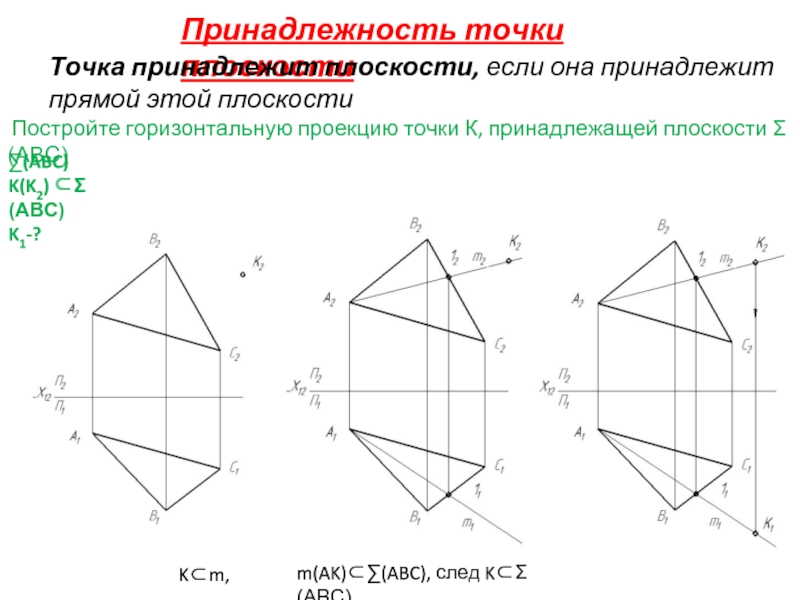
Слайд 10Принадлежность точки плоскости
Точка принадлежит плоскости, если она принадлежит прямой этой плоскости
m(AK)⊂∑(ABC), след K⊂Σ(ABC)
K⊂m,
∑(ABC)
K(K2) ⊂Σ(ABC)
K1-?
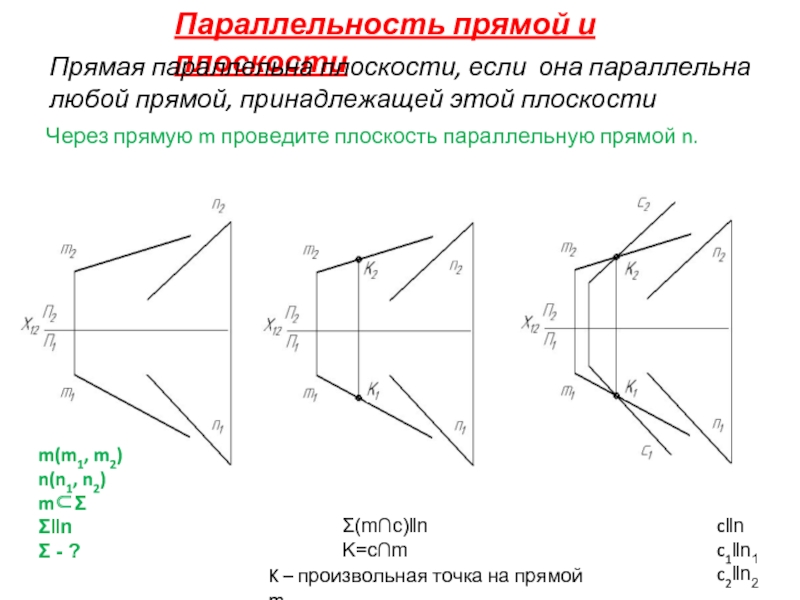
Слайд 11Параллельность прямой и плоскости
Прямая параллельна плоскости, если она параллельна любой прямой,
Через прямую m проведите плоскость параллельную прямой n.
m(m1, m2)
n(n1, n2)
m⊂Σ
Σ‖n
Σ - ?
Σ(m∩c)‖n
K=c∩m
c‖n
c1‖n1
c2‖n2
K – произвольная точка на прямой m
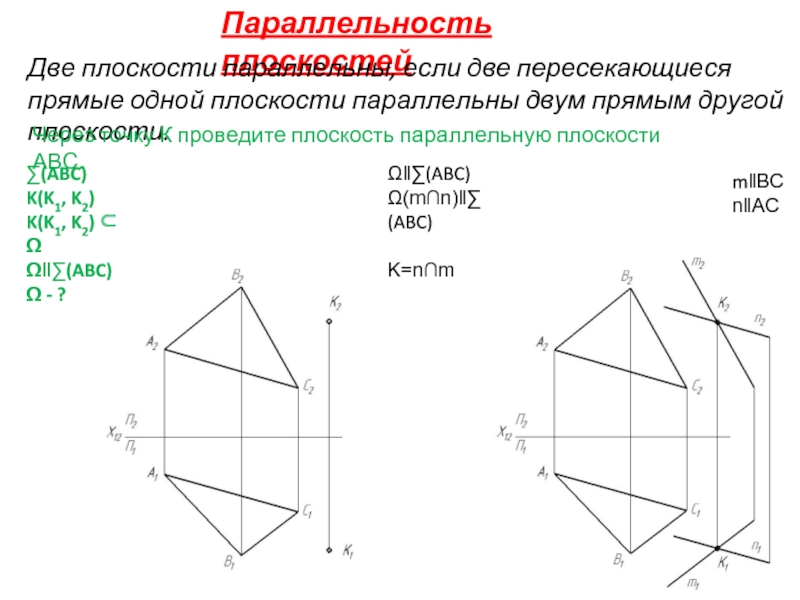
Слайд 12Параллельность плоскостей
Две плоскости параллельны, если две пересекающиеся прямые одной плоскости параллельны
Через точку К проведите плоскость параллельную плоскости АВС.
∑(ABC)
K(K1, K2)
K(K1, K2) ⊂ Ω
Ω‖∑(ABC)
Ω - ?
Ω‖∑(ABC)
Ω(m∩n)‖∑(ABC)
K=n∩m
m‖BC
n‖AC
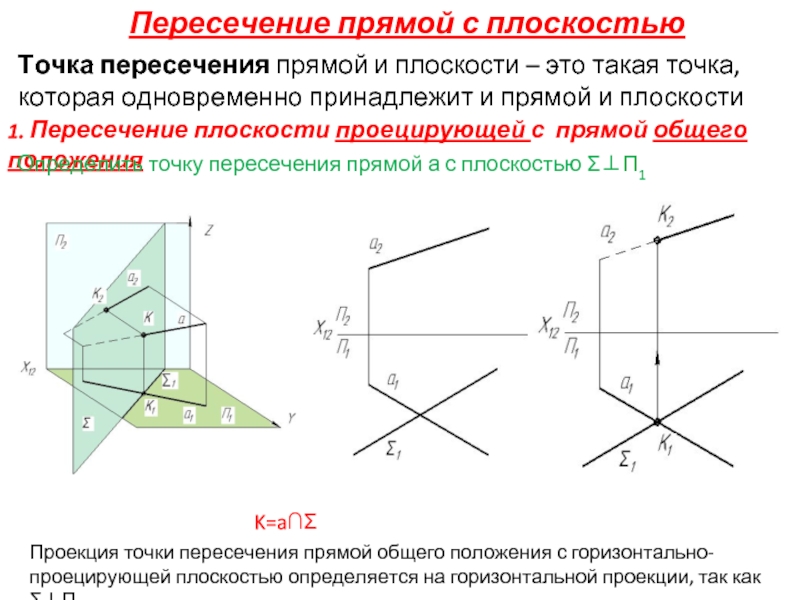
Слайд 13Пересечение прямой с плоскостью
1. Пересечение плоскости проецирующей с прямой общего положения
K=a∩Σ
Проекция точки пересечения прямой общего положения с горизонтально-проецирующей плоскостью определяется на горизонтальной проекции, так как Σ⊥П1
Точка пересечения прямой и плоскости – это такая точка, которая одновременно принадлежит и прямой и плоскости
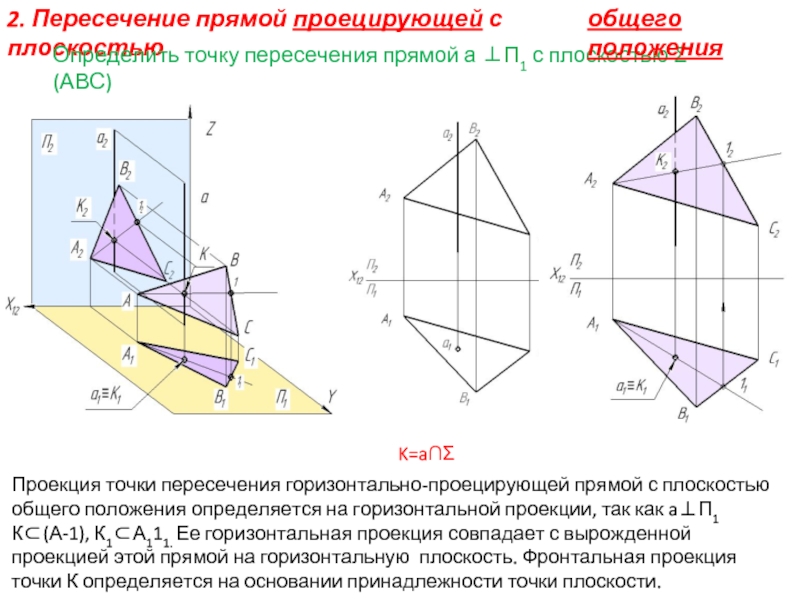
Слайд 142. Пересечение прямой проецирующей с плоскостью
Определить точку пересечения прямой а ⊥П1
Проекция точки пересечения горизонтально-проецирующей прямой с плоскостью
общего положения определяется на горизонтальной проекции, так как a⊥П1
К⊂(А-1), К1⊂А111. Ее горизонтальная проекция совпадает с вырожденной проекцией этой прямой на горизонтальную плоскость. Фронтальная проекция точки К определяется на основании принадлежности точки плоскости.
общего положения
K=a∩Σ
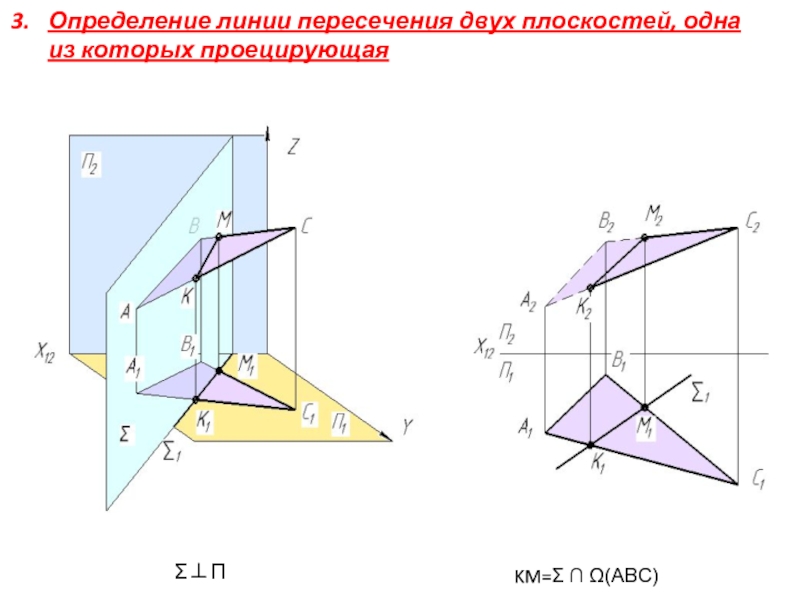
Слайд 15Определение линии пересечения двух плоскостей, одна из которых проецирующая
Σ⊥П1
KM=Σ ∩
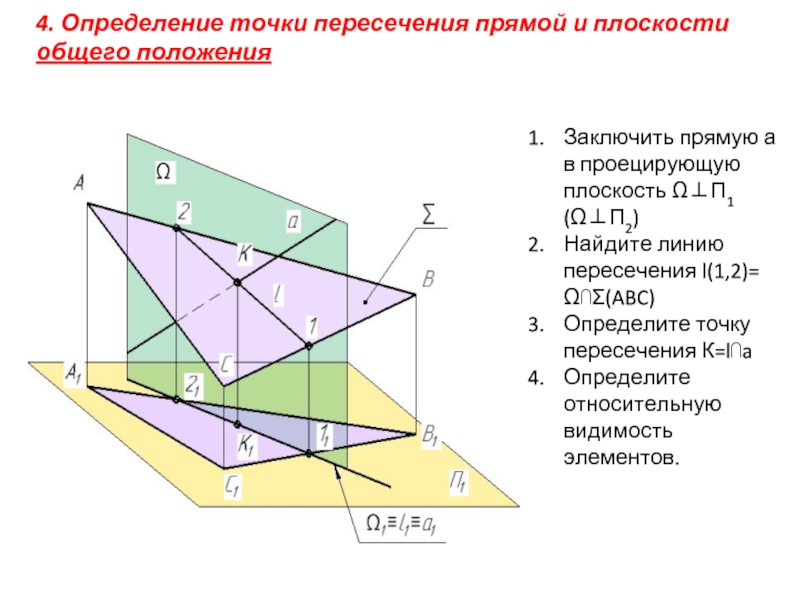
Слайд 164. Определение точки пересечения прямой и плоскости общего положения
Заключить прямую
Найдите линию пересечения l(1,2)= Ω⋂Σ(ABC)
Определите точку пересечения К=l⋂a
Определите относительную видимость элементов.
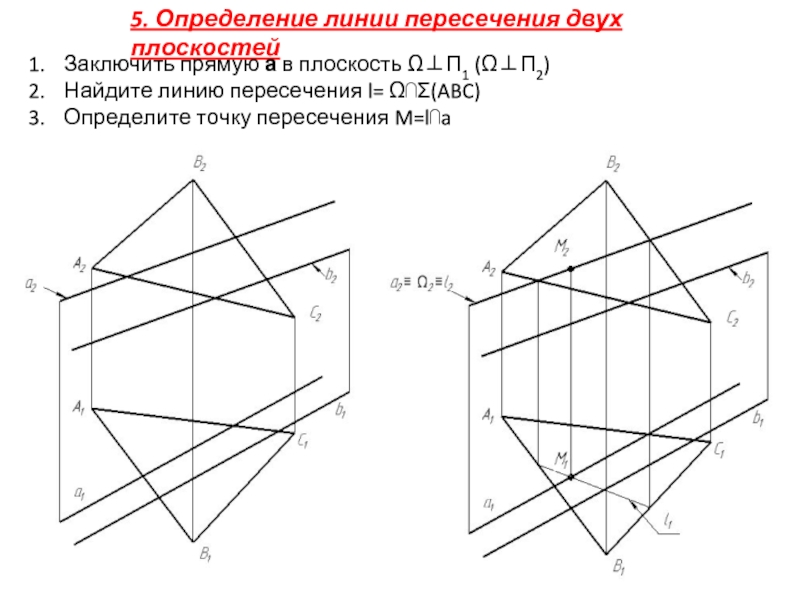
Слайд 185. Определение линии пересечения двух плоскостей
Заключить прямую а в плоскость Ω⊥П1
Найдите линию пересечения l= Ω⋂Σ(ABC)
Определите точку пересечения M=l⋂a
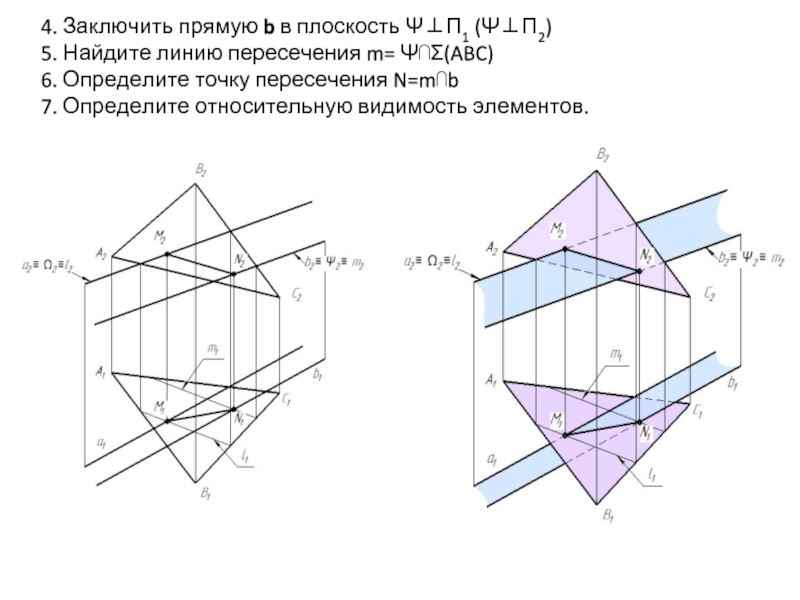
Слайд 194. Заключить прямую b в плоскость Ψ⊥П1 (Ψ⊥П2)
5. Найдите линию пересечения
6. Определите точку пересечения N=m⋂b
7. Определите относительную видимость элементов.
Слайд 206. Определение линии пересечения двух плоскостей методом секущих плоскостей
Проведите плоскость Г//П1
Постройте линии пересечения: m=Г⋂ Σ(а ⋂b); n=Г⋂ Ω
Определите точку пересечения М=m⋂n
Проведите плоскость Δ//П1
Постройте линии пересечения:
k= Δ ⋂ Σ(а ⋂b); j= Δ ⋂ Ω
Определите точку пересечения N=k⋂j
MN= Г ⋂ Δ
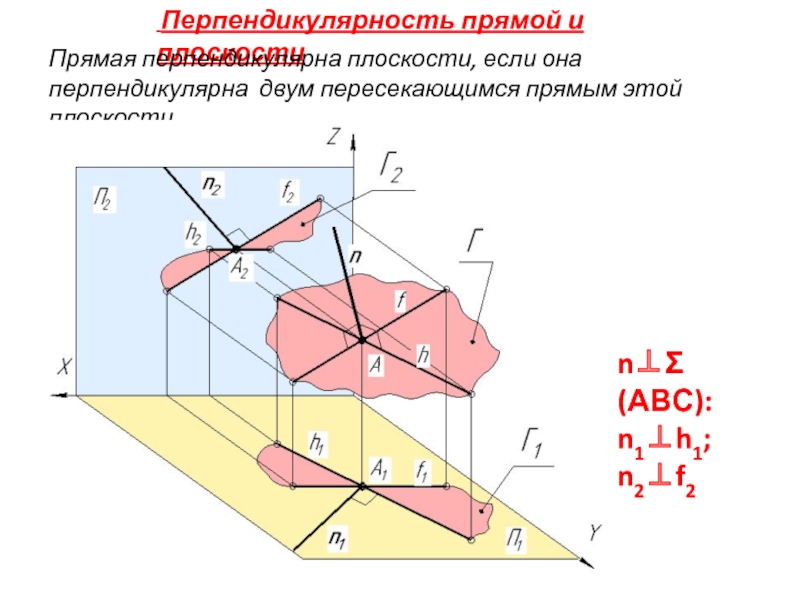
Слайд 21 Перпендикулярность прямой и плоскости
Прямая перпендикулярна плоскости, если она перпендикулярна двум
n⊥Σ(АВС):
n1⊥h1; n2⊥f2
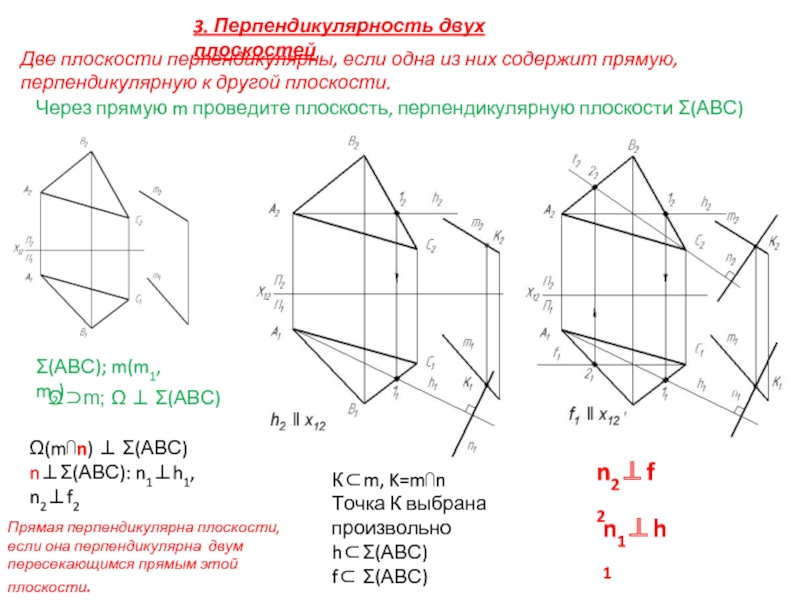
Слайд 233. Перпендикулярность двух плоскостей
Две плоскости перпендикулярны, если одна из них содержит
Через прямую m проведите плоскость, перпендикулярную плоскости Σ(АВС)
Ω(m⋂n) ⊥ Σ(АВС)
n⊥Σ(АВС): n1⊥h1, n2⊥f2
К⊂m, K=m⋂n
Точка К выбрана
произвольно
h⊂Σ(АВС)
f⊂ Σ(АВС)
n2⊥f2
Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым этой плоскости.
Σ(АВС); m(m1, m2)
Ω⊃m; Ω ⊥ Σ(АВС)
n1⊥h1
Слайд 244. Перпендикулярность прямых
Две прямые перпендикулярны, если одну из них можно заключить
Через точку М проведите прямую перпендикулярную а.
Через произвольную
точку К проведите
плоскость Σ(h⋂f) ⊥a;
В плоскости Σ(h⋂f)
проведите
прямую b⊂Σ(h⋂f).
Через точку М проведите
n параллельно b.