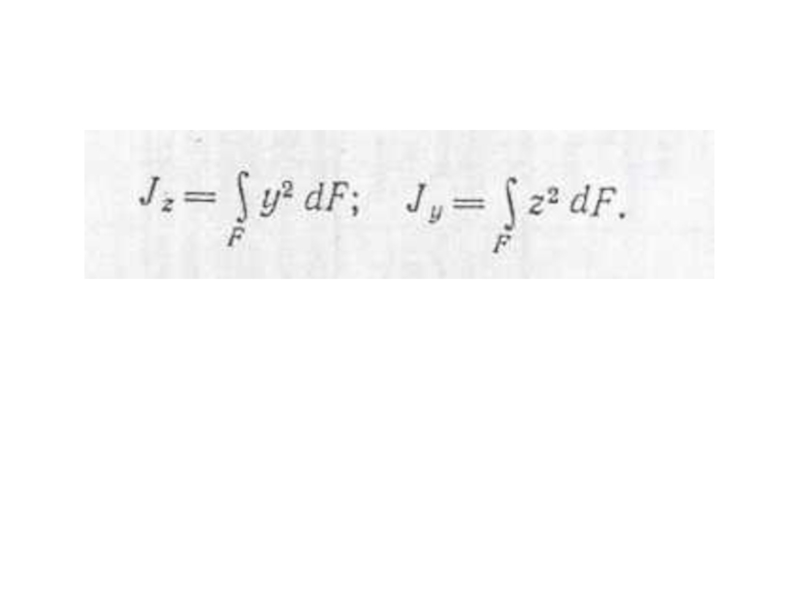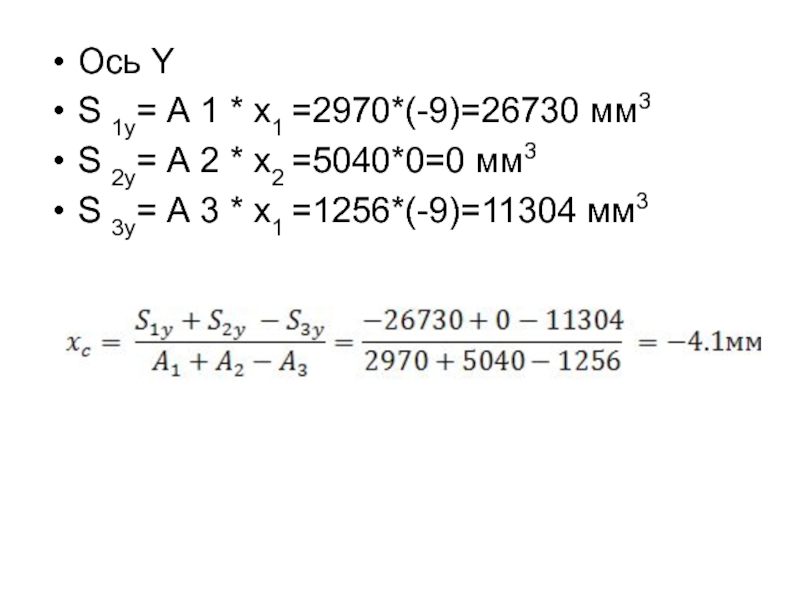- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Геометрические характеристики сечений презентация
Содержание
- 1. Геометрические характеристики сечений
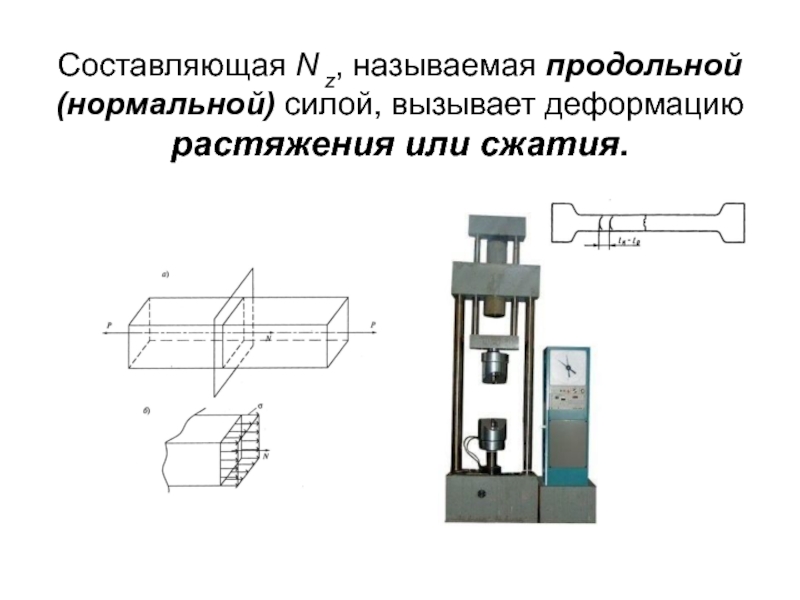
- 2. Составляющая N z, называемая продольной (нормальной) силой, вызывает деформацию растяжения или сжатия.
- 3. При деформации растяжения сжатия площадь поперечного сечений полностью характеризовала прочность и жесткость детали.
- 4. Момент M z скручивающий тело называют крутящим Кручение
- 5. Моменты M x и M y изгибают тело и называются изгибающими. Изгиб.
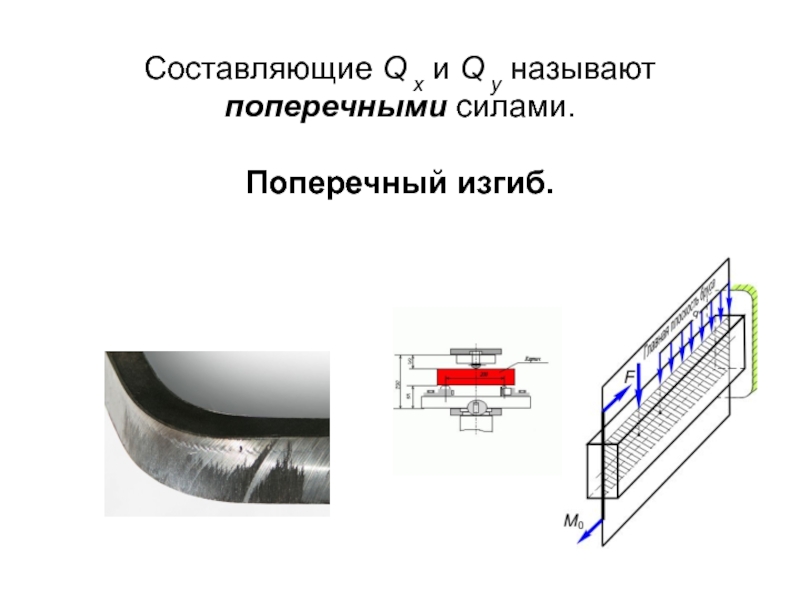
- 6. Составляющие Q x
- 7. Однако при деформации изгиба и кручения прочность
- 8. Статические моменты площадей Координаты zc и
- 10. Статический момент площади фигуры относительно какой-либо оси
- 11. Различают осевые, полярные и центробежные моменты инерции.
- 13. Полярным моментом инерции (моментом инерции относительно полюса)
- 14. Центробежным моментом инерции сечения называют взятую по
- 15. Из приведенных определений следует, что момент инерции
- 16. Момент инерции сечения относительно какой-либо оси равен
- 17. Центробежным моментом инерции сечения называют взятую по
- 19. Две взаимно перпендикулярные оси с началом в
- 20. главные центральные оси инерции фигуры могут быть
- 21. Моменты инерции относительно главных центральных осей инерции
- 22. Определим величины моментов инерции наиболее распространенных плоских сечений, встречающихся при расчетах и конструировании деталей механизмов.
- 23. Прямоугольник высотой h и шириной b. Выделим
- 24. Круговое кольцо с наружным диаметром D и
- 25. Обозначив d/D=C, после подстановки в
- 26. Для круга с учетом соотношения
- 27. Для кольца
- 29. Дано h1 = 45 мм b1
- 30. Статические моменты инерции относительно выбранных осей
- 31. Ось Y S 1y= А 1 *
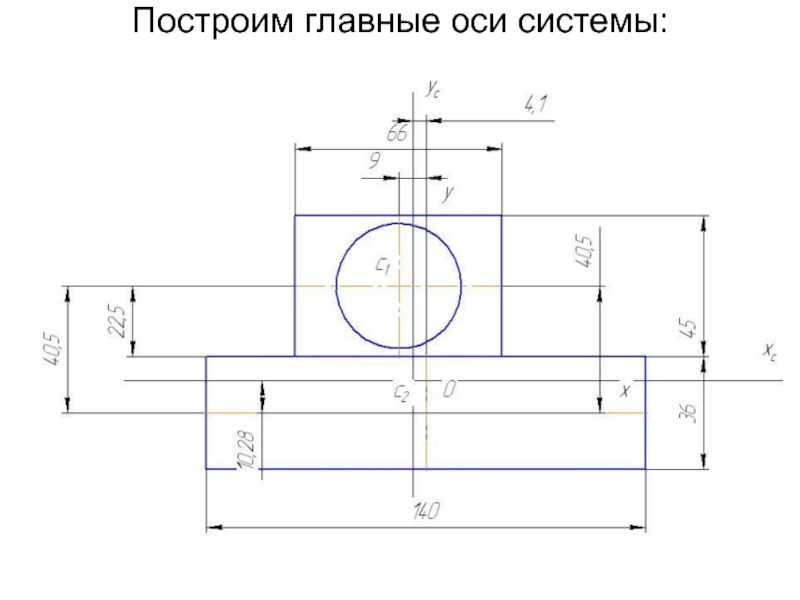
- 32. Построим главные оси системы:
- 33. Моменты инерции фигур относительно собственных осей: Ось X
- 34. Jxc = Jx1 +A1 *(y1 -yc )2
- 35. Ось Y
- 36. Jyc = Jy1 +A1 *(x1 -xc )2
- 37. Jxy2=A2 * (a2 -yc ) *(b2 -xc
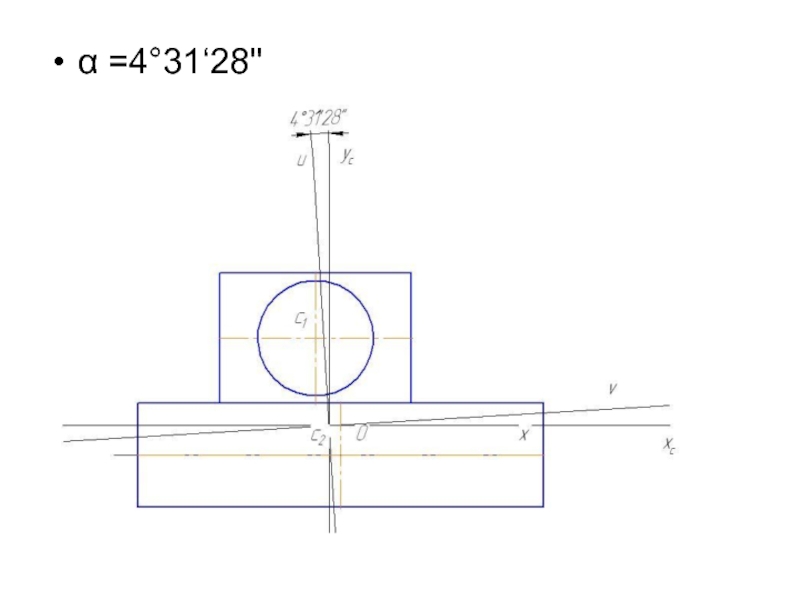
- 38. Определим угол поворота
- 39. α =4°31‘28''
- 40. Определим моменты инерции относительно главных осей:
- 42. Jmax = 11993195,12 мм4 Jmin = 52536,466 мм4
Слайд 2Составляющая N z, называемая продольной (нормальной) силой, вызывает деформацию растяжения или
сжатия.
Слайд 3При деформации растяжения сжатия площадь поперечного сечений полностью характеризовала прочность и
жесткость детали.
Слайд 7Однако при деформации изгиба и кручения прочность и жесткость характеризуются не
только размерами сечения, но и его формой. К числу геометрических характеристик сечения, учитывающих оба указанных фактора, относятся статические моменты, моменты инерции, моменты, сопротивления.
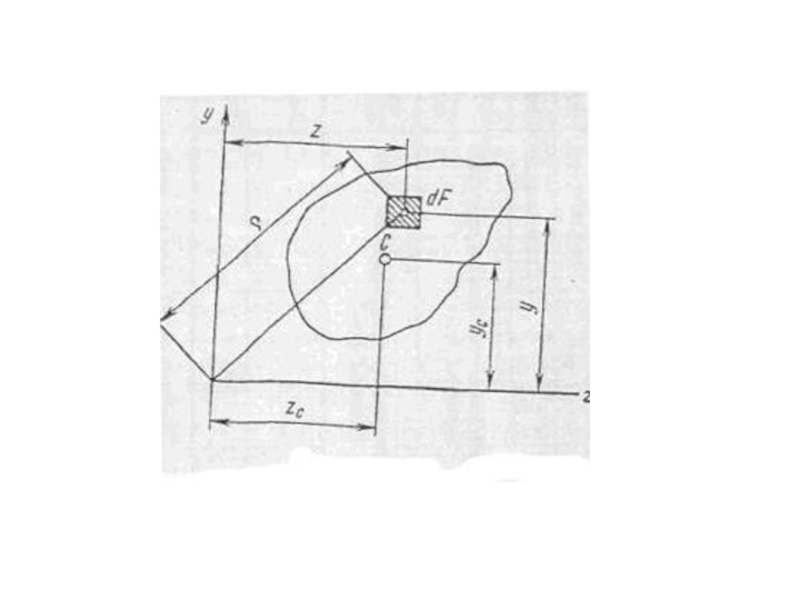
Слайд 8Статические моменты площадей
Координаты zc и ус центра тяжести плоской фигуры
определяются, как известно из общей механики формулами.
где F -площадь всей фигуры; dF - элемент площади.
где F -площадь всей фигуры; dF - элемент площади.
Слайд 10Статический момент площади фигуры относительно какой-либо оси равен сумме статических моментов
частей, из которых состоит фигура, относительно той же оси.
Оси, проходящие через центр тяжести фигуры, называют центральными осями. Статические моменты площадей относительно центральных осей равны нулю, так как zc = 0 или ус = 0.
Оси, проходящие через центр тяжести фигуры, называют центральными осями. Статические моменты площадей относительно центральных осей равны нулю, так как zc = 0 или ус = 0.
Слайд 11Различают осевые, полярные и центробежные моменты инерции.
Осевым моментом инерции сечения
называют взятую по всей площади сечения сумму произведений элементарных площадок на квадраты их расстояний до соответствующей оси. Обозначая моменты у инерции относительно осей z и y соответственно через J z и J y
Слайд 13Полярным моментом инерции (моментом инерции относительно полюса) называют взятую по всей
площади сечения сумму произведений элементарных площадок на квадраты их расстояний до данного полюса
Слайд 14Центробежным моментом инерции сечения называют взятую по всей площади сечения сумму
произведений элементарных пло-щадок на обе координаты в данной прямоугольной системе осей. Обозначая центробежный момент инерции через J zy имеем
Слайд 15Из приведенных определений следует, что момент инерции сложной фигуры равен сумме
моментов инерции ее частей.
Полярный момент инерции относительно полюса, являющегося началом прямоугольной системы координат, равен сумме моментов инерции относительно осей данной системы
Полярный момент инерции относительно полюса, являющегося началом прямоугольной системы координат, равен сумме моментов инерции относительно осей данной системы
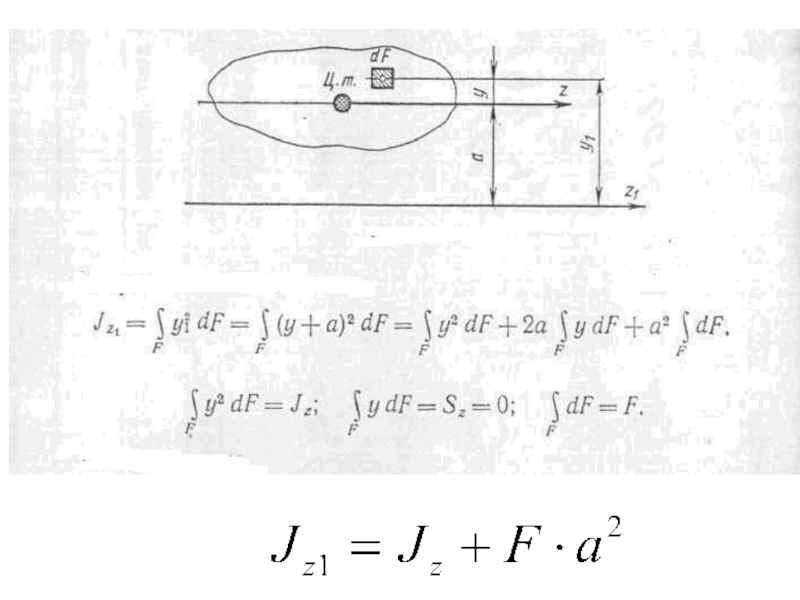
Слайд 16Момент инерции сечения относительно какой-либо оси равен моменту инерции этого сечения
относительно центральной оси, параллельной данной, сложенному с произведением площади сечения на квадрат расстояния между осями
Слайд 17Центробежным моментом инерции сечения называют взятую по всей площади сечения сумму
произведений элементарных площадок на обе координаты в данной прямоугольной системе осей.
Центробежный момент инерции J zy
Центробежный момент инерции J zy
Слайд 19Две взаимно перпендикулярные оси с началом в данной точке, для которых
центробежный момент инерции плоской фигуры равен нулю, называют главными осями инерции фигуры в этой точке.
Глазные оси инерции в центре тяжести фигуры называют главными центральными осями инерции.
Если хотя бы одна из двух взаимно перпендикулярных осей, проходящих через центр тяжести сечения, является осью симметрии, то такие оси являются главными центральными осями инерции.
Глазные оси инерции в центре тяжести фигуры называют главными центральными осями инерции.
Если хотя бы одна из двух взаимно перпендикулярных осей, проходящих через центр тяжести сечения, является осью симметрии, то такие оси являются главными центральными осями инерции.
Слайд 20главные центральные оси инерции фигуры могут быть найдены, если известны ее
центробежный J zy и осевые Jz и Jy моменты инерции относительно произвольно расположенных центральных осей z и у. Для этого систему осей zу необходимо повернуть на угол α, определяемый из соотношения.
Слайд 21Моменты инерции относительно главных центральных осей инерции называют главными моментами инерции:
они обладают тем свойством, что один из них имеет максимальное, а другой минимальное значение по сравнению с моментами инерции относительно остальных центральных осей.
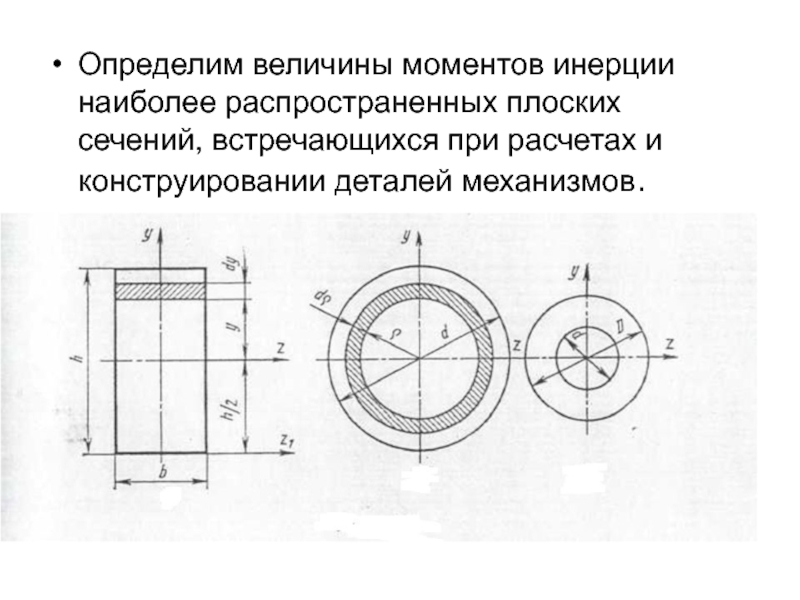
Слайд 22Определим величины моментов инерции наиболее распространенных плоских сечений, встречающихся при расчетах
и конструировании деталей механизмов.
Слайд 23Прямоугольник высотой h и шириной b. Выделим в прямоугольнике элементарную полоску
высотой dy и шириной b. Полоска отстоит от центральной оси г, параллельной основанию на расстоянии у, gри этом у изменяется в пределах
от + h/ 2 до - h/2
от + h/ 2 до - h/2
Слайд 24Круговое кольцо с наружным диаметром D и внутренним d.
В данном случае
полярный момент инерции может быть получен как разность полярных моментов инерции большого и малого круга
Слайд 25Обозначив d/D=C, после подстановки в выражение‘ получим из соотношения
находим осевые моменты инерции круга и кругового кольца
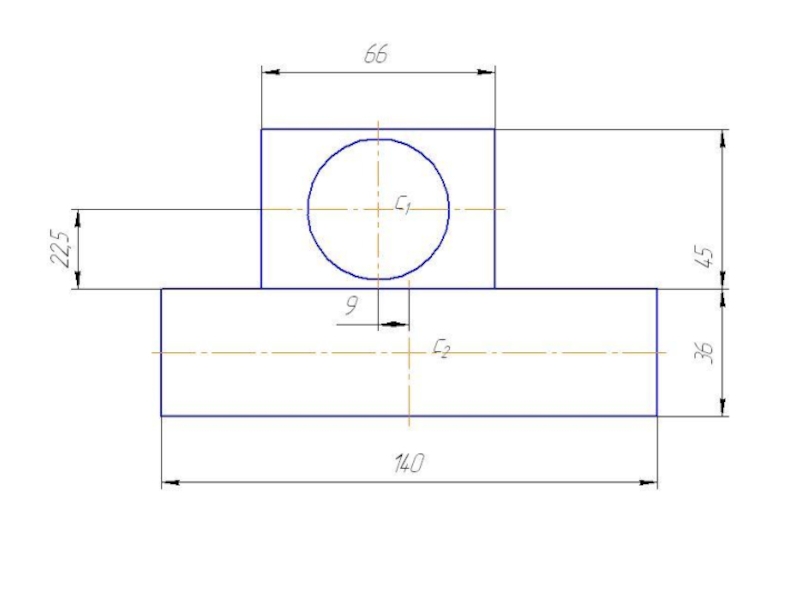
Слайд 29 Дано
h1 = 45 мм
b1 = 66 мм
h2 = 36 мм
b2=
140 мм
Отверстие d = 40 мм
Площади фигур
А 1 = h1* b1=45*66=2970 мм2
А 2 = h2* b2=36*140=5040 мм2
А 3 = πd2/4=3.14* 402 / 4 = 1256 мм2
Отверстие d = 40 мм
Площади фигур
А 1 = h1* b1=45*66=2970 мм2
А 2 = h2* b2=36*140=5040 мм2
А 3 = πd2/4=3.14* 402 / 4 = 1256 мм2
Слайд 30Статические моменты инерции относительно выбранных осей
Ось X
S 1x= А 1
* y1 =2970*40.5=120285 мм3
S 2x= А 2 * y2 =5040*0=0 мм3
S 3x= А 3 * y3 =1256*40.5=50868 мм3
S 2x= А 2 * y2 =5040*0=0 мм3
S 3x= А 3 * y3 =1256*40.5=50868 мм3
Слайд 31Ось Y
S 1y= А 1 * x1 =2970*(-9)=26730 мм3
S 2y= А
2 * x2 =5040*0=0 мм3
S 3y= А 3 * x1 =1256*(-9)=11304 мм3
S 3y= А 3 * x1 =1256*(-9)=11304 мм3
Слайд 34Jxc = Jx1 +A1 *(y1 -yc )2 -Jx2 - A2
*(y2 -yc )2+ Jx3 + A3 *(y3 -yc )2 =
= 1078110+2670*(40.5-10.277)2 -125600 – 1256*(40.5 -10.277) 2 +8232000 +
5040*(0-10.277)2 = 11007151,55мм4
= 1078110+2670*(40.5-10.277)2 -125600 – 1256*(40.5 -10.277) 2 +8232000 +
5040*(0-10.277)2 = 11007151,55мм4
Слайд 36Jyc = Jy1 +A1 *(x1 -xc )2 –Jy2 - A2
*(x2 -xc )2+ Jy3 + A3 *(x3 -xc )2 =
= 501187.5+2670*(9-4.1)2 -125600 – 1256*(9 -4.1) 2 +544320 +
5040*(0-4.1)2 = 1038580,04 мм4
Центробежные момент инерции:
Jxy1=A1 * (a1 -yc ) *(b1 -xc )=2670*(40.5-10.277)*(9-4.1)=395407,509 мм4
= 501187.5+2670*(9-4.1)2 -125600 – 1256*(9 -4.1) 2 +544320 +
5040*(0-4.1)2 = 1038580,04 мм4
Центробежные момент инерции:
Jxy1=A1 * (a1 -yc ) *(b1 -xc )=2670*(40.5-10.277)*(9-4.1)=395407,509 мм4
Слайд 37Jxy2=A2 * (a2 -yc ) *(b2 -xc )=1256*(40.5-10.277)*(9-4.1)=186004,4 мм4
Jxy3=A3 * (a3
-yc ) *(b3 -xc )=5040*(0-10.277)*(0-4.1)=212363,93 мм4
Jxy = Jxy1 + Jxy 3- Jxy2 =395407,509+212363,93-186004,4=793775,839мм4
Jxy = Jxy1 + Jxy 3- Jxy2 =395407,509+212363,93-186004,4=793775,839мм4