- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математические задачи компьютерной томографии презентация
Содержание
- 1. Математические задачи компьютерной томографии
- 2. Преобразование Радона — интегральное преобразование функции
- 13. Двумерное преобразование Фурье. Формула обращения. Двумерное преобразование
- 14. Обозначим новые переменные s = xcosα
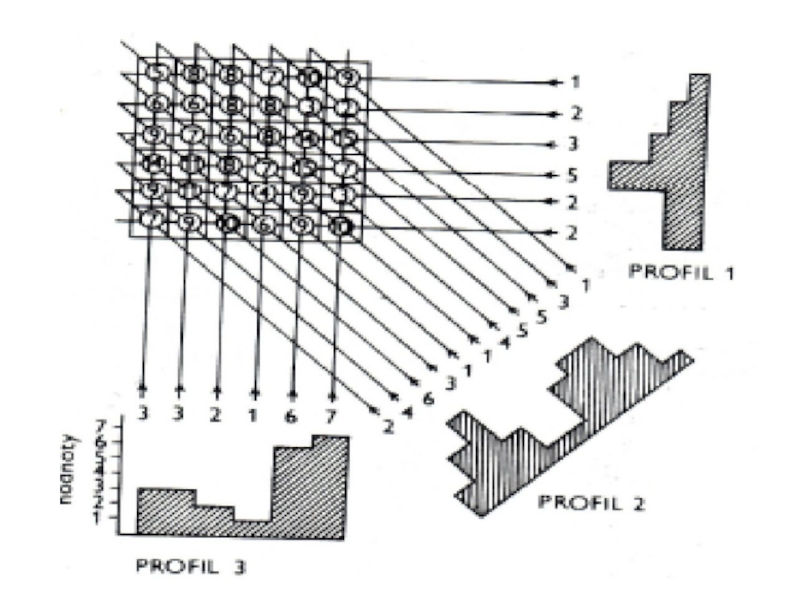
- 15. Получение компьютерной томограммы Получение компьютерной томограммы
- 16. РАЗРЕШАЮЩАЯ СПОСОБНОСТЬ Компьютерный томограф обладает двумя видами
- 17. ОТНОШЕНИЕ СИГНАЛ/ШУМ (ОСШ) Квантовая эффективность детектора η
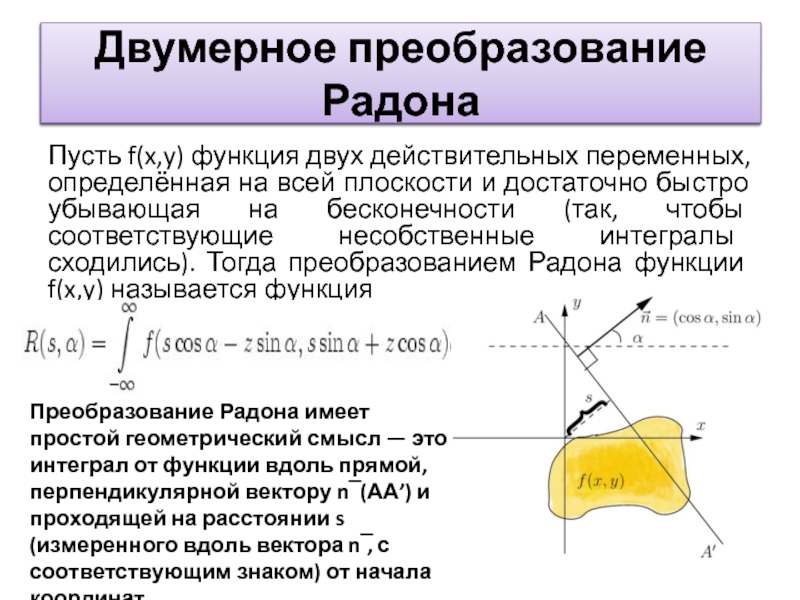
- 19. Двумерное преобразование Радона Пусть f(x,y) функция двух
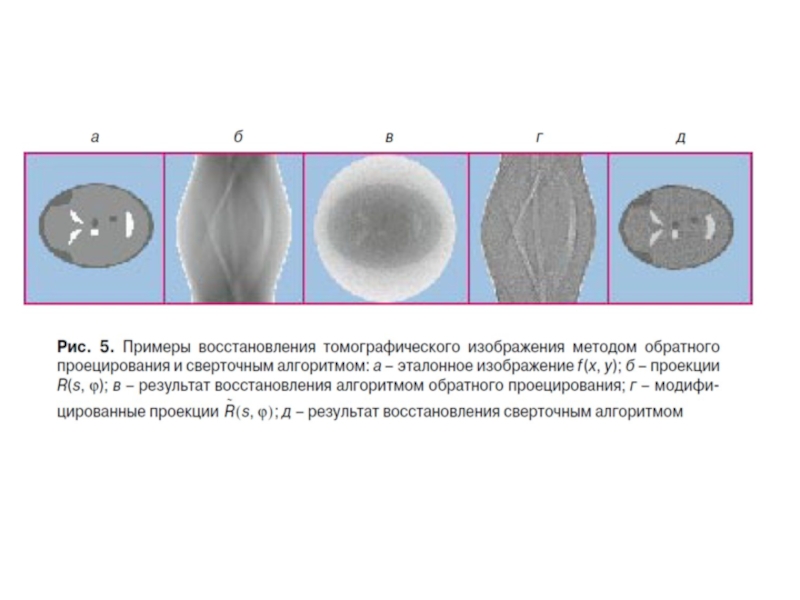
- 20. Артефакты При эффекте неполного заполнения Ужесточение излучения Движения пациента
- 23. Двумерное преобразование Фурье.
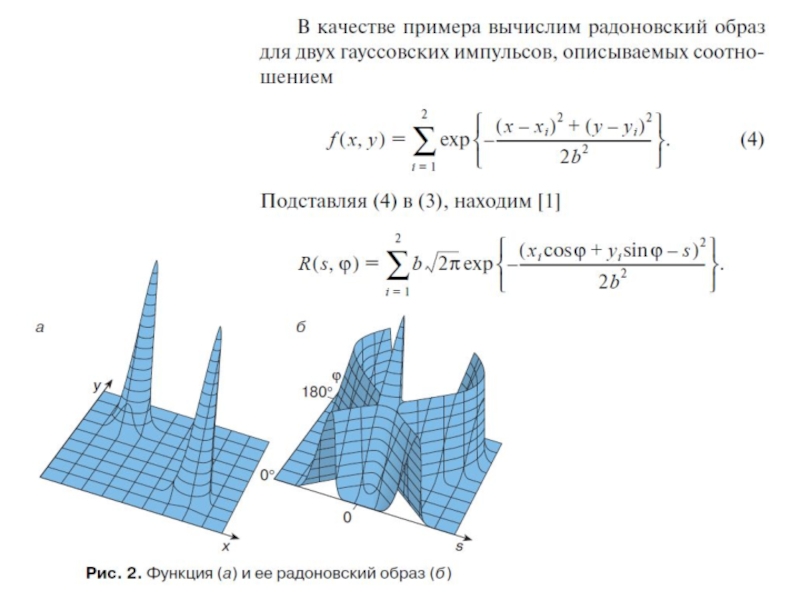
Слайд 2Преобразование Радона
— интегральное преобразование функции многих переменных, родственное преобразованию Фурье.
Важнейшее свойство преобразования Радона — обратимость, то есть возможность восстанавливать исходную функцию по её преобразованию Радона.
Слайд 13Двумерное преобразование Фурье. Формула обращения.
Двумерное преобразование Фурье от функции f(x,y)
Формула обращения
в полярных координатах
Слайд 14Обозначим новые переменные s = xcosα + ysinα, z = −
Таким образом, одномерное преобразование Фурье по переменной s от преобразования Радона функции f даёт нам двумерное преобразование Фурье от функции f. Формула обращения преобразования Радона
или
.
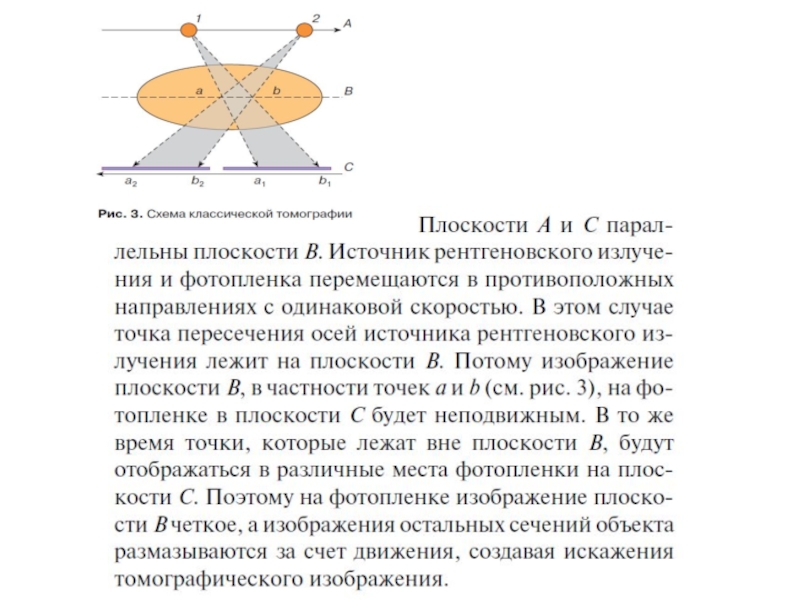
Слайд 15Получение компьютерной томограммы
Получение компьютерной томограммы основывается на выполнении следующих операций:
* формирования
* сканирования объекта пучком рентгеновского излучения, осуществляемого движением (вращательным и поступательным) вокруг пациента устройства излучатель – детекторы;
* измерения излучения и определения его ослабления с последующим преобразованием результатов в цифровую форму;
* машинного (компьютерного) синтеза томограммы по совокупности данных измерения, относящихся к выбранному слою;
* построения изображения исследуемого слоя на экране видеомонитора (дисплея).
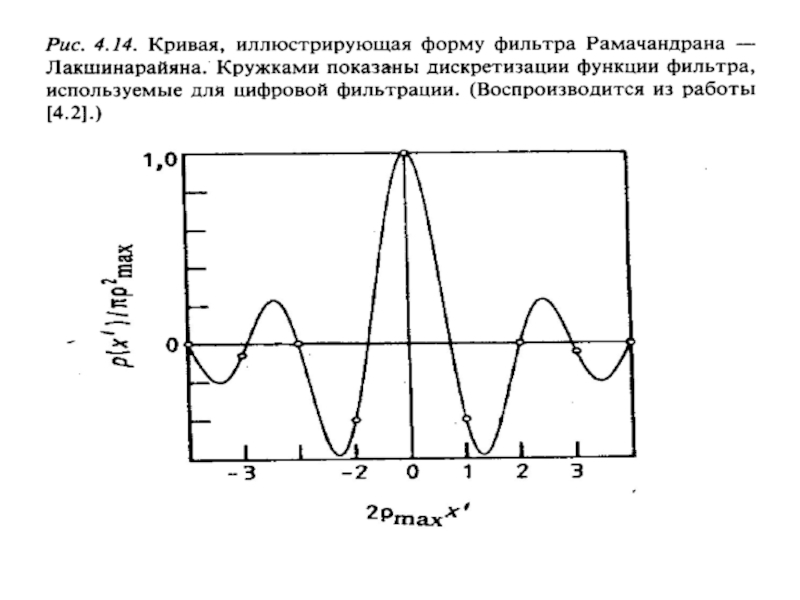
Слайд 16РАЗРЕШАЮЩАЯ СПОСОБНОСТЬ
Компьютерный томограф обладает двумя видами разрешающей способности: пространственной и по
Слайд 19Двумерное преобразование Радона
Пусть f(x,y) функция двух действительных переменных, определённая на всей
Преобразование Радона имеет простой геометрический смысл — это интеграл от функции вдоль прямой, перпендикулярной вектору n ̅ (АА’) и проходящей на расстоянии s (измеренного вдоль вектора n ̅, с соответствующим знаком) от начала координат.
Двумерное преобразование Радона