Подготовили:
Бедрак Анастасия
Хмелевская Анна
Натальченко Полина
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Функции (виды функций и их графики) презентация
Содержание
- 1. Функции (виды функций и их графики)
- 2. Степенная функция
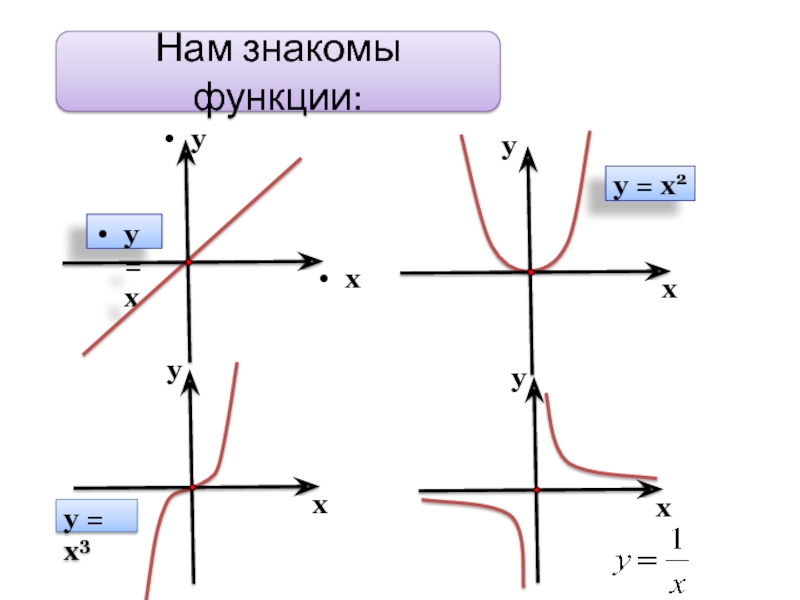
- 3. Нам знакомы функции:
- 4. Определение: Степенной функцией называется функция вида
- 5. у х 1 0
- 6. Степенная функция: Показатель р = 2n –
- 7. Показатель р = 2n-1 – нечетное натуральное
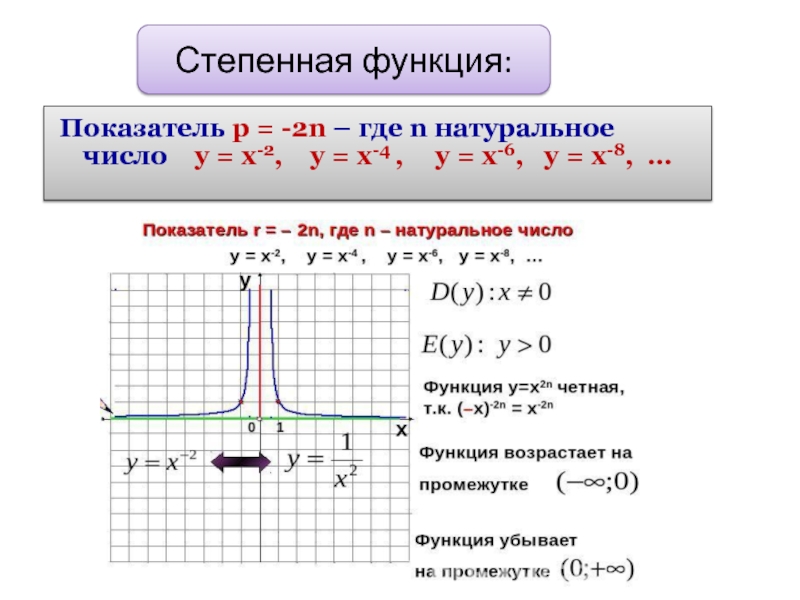
- 8. Показатель р = -2n – где n
- 9. Степенная функция: Показатель р = -2n –
- 10. Показатель р = -(2n-1) – где n
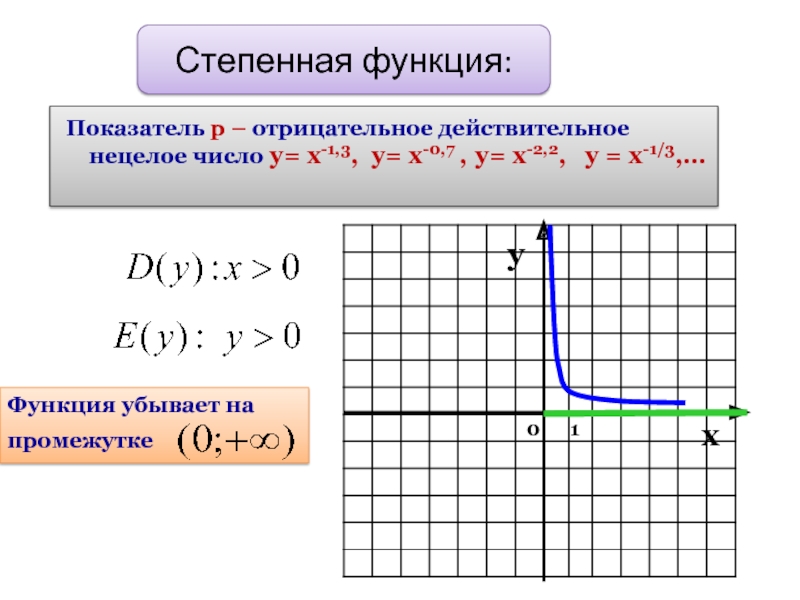
- 11. Показатель р – отрицательное действительное нецелое число
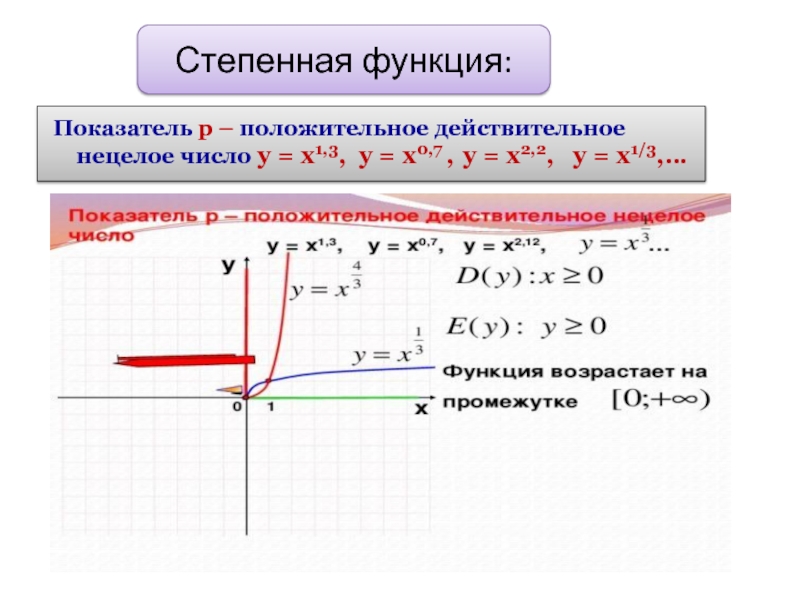
- 12. Степенная функция: Показатель р – положительное действительное
- 13. Показательная функция: Определение. Функция, заданная
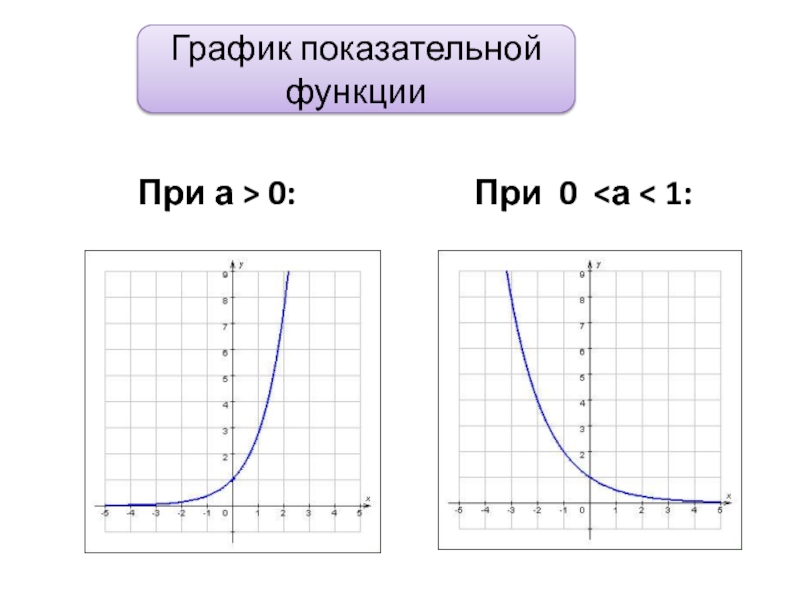
- 14. График показательной функции При а > 0: При 0
- 15. Свойства показательной функции при а>0: 1.Область определения
- 16. Свойства функции При а >1, 0 < а
- 17. А. Дистервег „Развитие и образование
Слайд 1 « Функции»
(виды функций
и их
графики)
Слайд 4Определение:
Степенной функцией называется функция вида
у = х
где р – заданное действительное
число
Свойства и график степенной функции зависят от свойств степени с действительным показателем, и в частности от того, при каких значениях х и р имеет смысл степень хр.
Слайд 5
у
х
1
0
у = х2
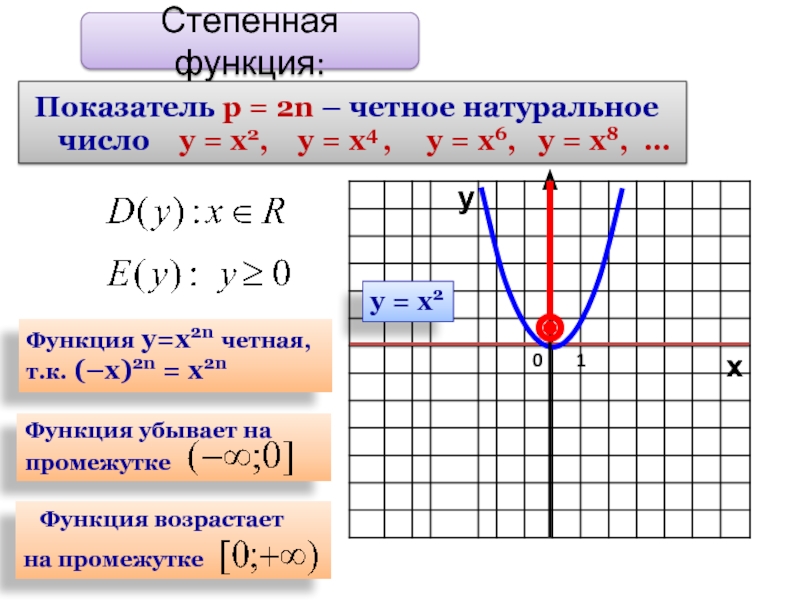
Степенная функция:
Показатель р = 2n – четное натуральное число
у = х2, у = х4 , у = х6, у = х8, …
Функция у=х2n четная,
т.к. (–х)2n = х2n
Функция убывает на
промежутке
Функция возрастает
на промежутке
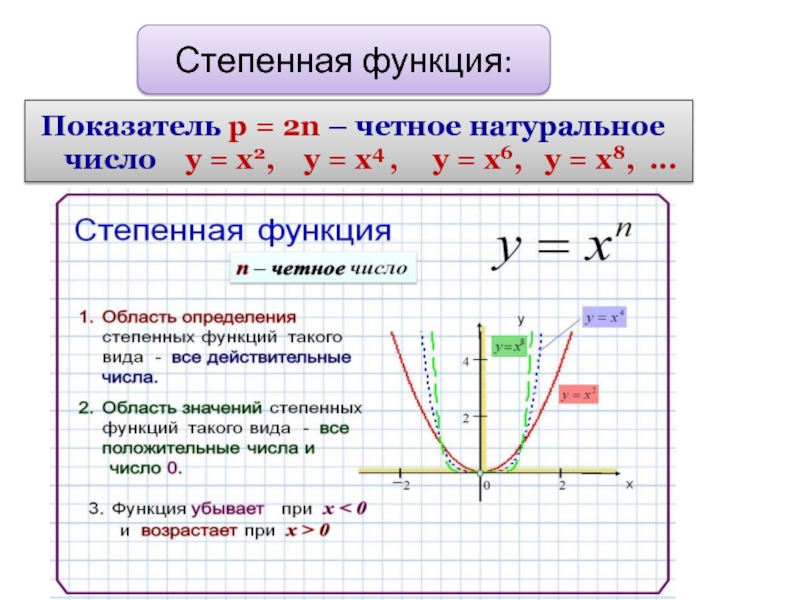
Слайд 6Степенная функция:
Показатель р = 2n – четное натуральное число у
= х2, у = х4 , у = х6, у = х8, …
Слайд 7Показатель р = 2n-1 – нечетное натуральное число у =
х3, у = х5 , у = х7, у = х9, …
Степенная функция:
Функция возрастает на
промежутке
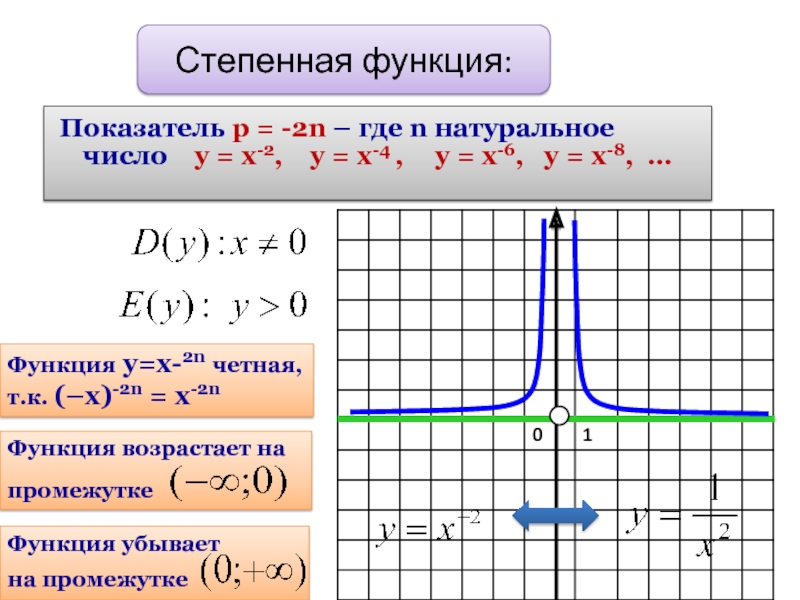
Слайд 8Показатель р = -2n – где n натуральное число у
= х-2, у = х-4 , у = х-6, у = х-8, …
Степенная функция:
Функция у=х-2n четная,
т.к. (–х)-2n = х-2n
Функция возрастает на
промежутке
0
1
Слайд 9Степенная функция:
Показатель р = -2n – где n натуральное число
у = х-2, у = х-4 , у = х-6, у = х-8, …
Слайд 10Показатель р = -(2n-1) – где n натуральное число у
= х-3, у = х-5 , у = х-7, у = х-9, …
Степенная функция:
Слайд 11Показатель р – отрицательное действительное нецелое число у= х-1,3, у= х-0,7
, у= х-2,2, у = х-1/3,…
Степенная функция:
0
1
у
х
Слайд 12Степенная функция:
Показатель р – положительное действительное нецелое число у = х1,3,
у = х0,7 , у = х2,2, у = х1/3,…
Слайд 13Показательная функция:
Определение.
Функция, заданная формулой у = ах (где а
> 0, а ≠ 1, х – показатель степени), называется показательной функцией с основанием а.
Слайд 15Свойства показательной функции
при а>0:
1.Область определения – множество действительных чисел.
2.Область значений –
множество положительных действительных чисел.
3.Функция возрастает на всей числовой прямой.
4.При х = 0, у = 1, график проходит через точку (0; 1)
3.Функция возрастает на всей числовой прямой.
4.При х = 0, у = 1, график проходит через точку (0; 1)
при 0 < а < 1:
1. Область определения – множество действительных чисел.
2. Область значений – множество положительных действительных чисел.
3. Функция убывает на всей числовой прямой.
4. При х = 0, у = 1, график проходит через точку ( 0 ; 1).
Слайд 16Свойства функции
При а >1, 0 < а
ах · ау = ах+у
2. ах : ау = ах-у
3. (а ·в)х = ах · вх
4. (а/в)х = ах/ вх
5. (ах)у = аху
2. ах : ау = ах-у
3. (а ·в)х = ах · вх
4. (а/в)х = ах/ вх
5. (ах)у = аху
Слайд 17А. Дистервег
„Развитие и образование ни одному человеку не могут
быть даны или сообщены. Всякий, кто желает к ним приобщиться, должен достигнуть этого собственной деятельностью, собственными силами, собственным напряжением”
Спасибо за внимание!!!
