Михайлова Ольга Юрьевна
E-mail: mikhajlova@mirea.ru
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Линейная алгебра и аналитическая геометрия презентация
Содержание
- 1. Линейная алгебра и аналитическая геометрия
- 2. Календарный план Учебный семестр длится до 7
- 3. Комментарии к календарному плану Все задания выполняются
- 4. Список литературы Высшая математика для экономистов: учебник
- 5. Базы данных, информационно-справочные и поисковые системы Справочно-информационная
- 6. Темы раздела линейная алгебра Тема 1. Система
- 7. Темы раздела аналитическая геометрия Тема 6. Элементы
- 8. Система линейных уравнений общего вида. Метод Жордана-Гаусса решения системы линейных уравнений. Тема 1
- 9. Система линейных уравнений. Понятие
- 10. Определения. О.1 Линейным уравнением (ЛУ) от n-переменных
- 11. Матрицы СЛУ. Основная матрица
- 12. Определения. О.7 СЛУ называется совместной, если она
- 13. О.9 Элементарными преобразованиями СЛУ называются следующие преобразования:
- 14. Рассмотрим преобразование типа (в)
- 15. Определения. О.10 Переменная в
- 17. Определения. О.11 Общим
- 18. Метод Жордана-Гаусса решения СЛУ Приведение системы линейных
- 21. Формулы преобразований Жордана – Гаусса: Элементы
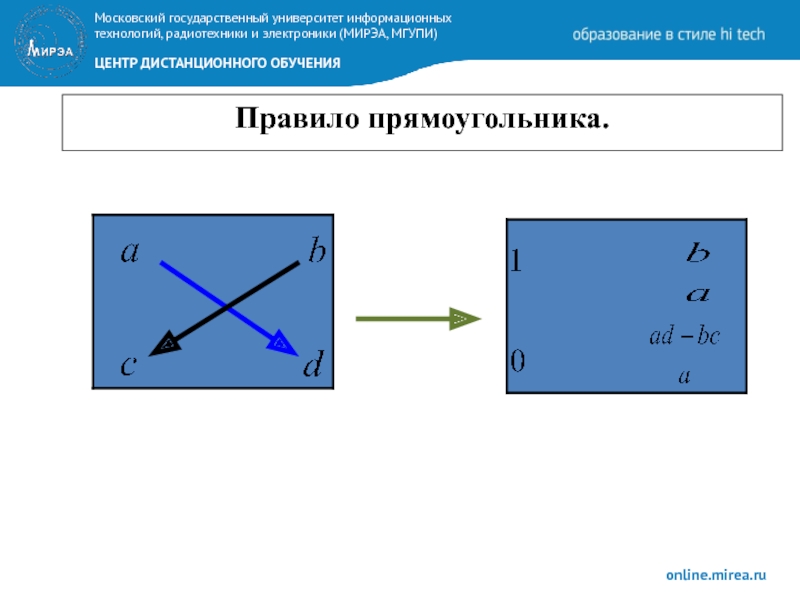
- 22. Правило прямоугольника.
- 23. Свойства преобразований Ж-Г. Л 2.1.
- 24. Алгоритм Жордана – Гаусса. Выберем уравнение, не
- 25. Анализ работы по методу Жордана - Гаусса.
- 26. Арифметическое n-мерное векторное пространство. Линейная зависимость и независимость системы векторов. Тема 2
- 27. Арифметическое n-мерное векторное пространство.
- 28. Определения О.5.1 Арифметическим вектором размерности n называется
- 29. Т.5.1 Выше перечисленные операции
- 30. О.5.3 Множество V , на котором
- 31. Определения О.5.4 Линейной комбинацией векторов
- 32. О.5.5 Упорядоченный набор векторов называется системой
- 33. Свойства линейной независимости и зависимости С.1 Линейная
- 35. Базис и ранг системы векторов Базис
- 36. Определения О.6.1. Подсистема Т:
- 37. О.6.3.Рангом системы векторов называется число векторов
- 38. Ранг и его свойства С.1. Ранг системы
- 39. О.6.4. Рангом матрицы А мы будем называть
- 40. Алгоритм вычисления ранга и нахождения базиса Составить
- 41. Матрицы. Операции над матрицами. Обратная матрица. Способы ее нахождения. Тема 3
- 42. Операции над матрицами. Матрицы. Операции
- 43. Определения. О.9.1 Матрицей размерности n x m
- 44. На множестве
- 45. Свойства операции сложения матриц: С.1 Коммутативность
- 46. О.9.4 Произведением матриц
- 47. О.9.5 Матрица называется квадратной порядка n,
- 48. О.9.7 Матрица
- 49. Алгоритм нахождения обратной матрицы: Расширить
- 50. Определители, их свойства и вычисление. Тема 4
- 51. Определители, их свойства и вычисление Определители
- 52. Определения. О.11.1 Определителем матрицы 2-го порядка
- 53. О.11.3 Минором
- 54. О.11.5 Определителем матрицы порядка n называется
- 55. Свойства определителей С.1 Определитель транспонированной матрицы равен
- 56. Алгоритм вычисления определителя n-го порядка с помощью
- 57. Л.12.1 Сумма произведений всех элементов строки
- 58. Алгоритм вычисления с помощью
- 59. Правило Крамера и матричный способ решения системы линейных уравнений. Тема 5
- 60. Различные способы решения квадратных СЛУ Правило Крамера
- 61. Найдем определитель матрицы системы: Правило Крамера решения квадратных СЛУ
- 62. Пусть ΔJ – определитель матрицы, полученной из
- 63. Матричная форма записи СЛУ. Матричный способ решения.
- 64. Тогда решением матричного уравнения будет матрица-столбец Х: Проверка:
- 65. Темы раздела аналитическая геометрия Тема 6. Элементы
- 66. Элементы векторной алгебры. Тема 6
- 67. Элементы векторной алгебры. Линейные операции над
- 68. Простейшие задачи аналитической геометрии. Тема 7
- 69. Простейшие задачи аналитической геометрии в
- 70. Уравнения прямой на плоскости и в пространстве. Тема 8
- 71. Уравнения прямой на плоскости и в пространстве.
- 72. Пусть прямая проходит через точку параллельно
- 73. и рассмотрим вектор Выберем на прямой произвольную
- 74. Пусть прямая проходит через две точки Выберем
- 75. Уравнение прямой на плоскости по точке и
- 76. уравнение прямой, проходящей через заданную точку и перпендикулярной заданному вектору
- 77. Уравнения плоскости в пространстве. Тема 9
- 78. Уравнения плоскости в пространстве. Уравнение плоскости
- 79. Пусть плоскость проходит
- 80. уравнение плоскости, проходящей через точку и параллельно двум векторам
- 81. Пусть задана плоскость, проходящая через три точки:
- 82. Уравнение плоскости по точке и нормальному вектору.
- 83. Пусть плоскость Р, проходит через заданную точку
- 84. уравнение плоскости, проходящей через заданную точку и перпендикулярной заданному вектору
- 85. Раскроем скобки в предыдущем уравнении: Обозначим: Общее уравнение плоскости общее уравнение плоскости
- 86. Взаимное расположение прямых и плоскостей. Тема 10
- 87. Взаимное расположение прямых и плоскостей. Взаимное
- 88. Пусть заданы две прямые Острый угол между
- 89. условия параллельности прямых условия перпендикулярности прямых
- 90. Пусть прямая задана уравнением:
- 91. Возможные случаи ориентации прямой и плоскости:
- 92. Календарный план Учебный семестр длится до 7
- 93. Желаю удачи!
Слайд 1Московский государственный университет информационных
технологий, радиотехники и электроники (МИРЭА, МГУПИ)
ЦЕНТР ДИСТАНЦИОННОГО ОБУЧЕНИЯ
Линейная
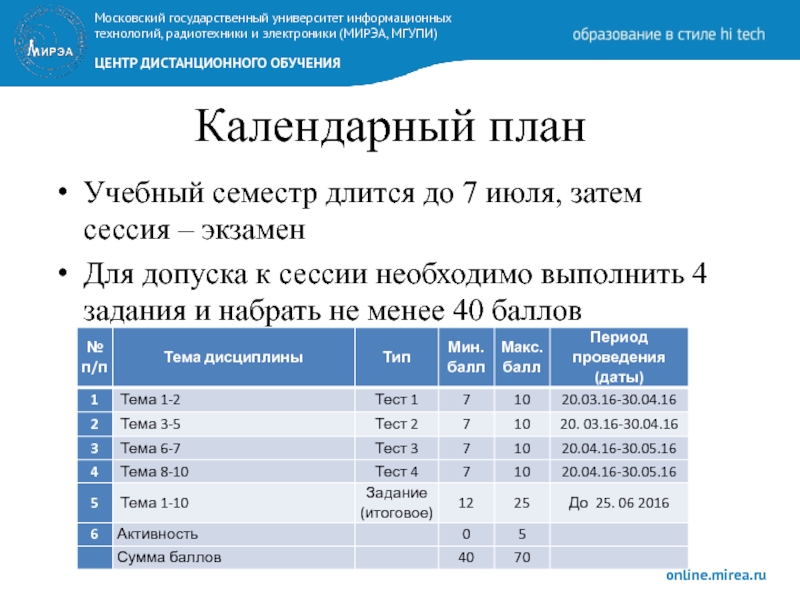
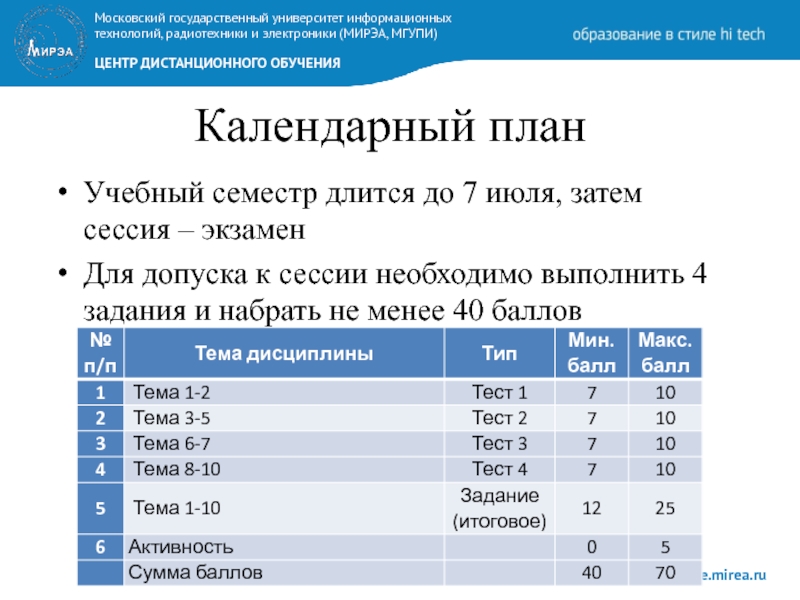
Слайд 2Календарный план
Учебный семестр длится до 7 июля, затем сессия – экзамен
Для
Слайд 3Комментарии к календарному плану
Все задания выполняются на Учебном портале online-edu.mirea.ru
Тесты выполняются
Задания выполняются в виде файла и прикрепляются на проверку на Учебном портале. Задания проверяются в период, указанный в календарном плане
По каждому заданию могут быть даны дополнительные вопросы и комментарии
Слайд 4Список литературы
Высшая математика для экономистов: учебник / под ред Н.Ш. Кремера
М.С. Красс, Б.П. Чупрынов. Основы математики и ее приложения в экономическом образовании. М. «Дело», 2003. – 625 с.
Высшая математика для экономистов: практикум / под ред Н.Ш. Кремера. – М.: ЮНИТИ, 2010. – 479 с.
Шипачев В.С. Высшая математика. Полный курс: учебник для бакалавров/ под ред А. Тихонова. – М.: Юрайт, 2012. – 479 с.
Высшая математика в упражнениях и задачах – 7-е изд. испр. – М.: ОНИКС; Мир и образование, 2008. – 816 с.
Клименко Ю.И. высшая математика для экономистов в примерах и задачах: учебник – 2-е изд. перераб. и доп. – М.: Экзамен, 2006. – 734 с.
Слайд 5Базы данных, информационно-справочные и поисковые системы
Справочно-информационная система Гарант, Консультант.
Электронная библиотечная система
Библиотека Genesis [Электронный ресурс]. – Электрон. дан. Режим доступа: http://gen.lib.rus.ec/.
Образовательный математический сайт [Электронный ресурс]. – Электрон. дан. – Режим доступа: http://www.exponenta.ru/.
Научная электронная библиотека [Электронный ресурс]. – Электрон. дан. – Режим доступа: http://www.elibrary.ru/.
Слайд 6Темы раздела линейная алгебра
Тема 1. Система линейных уравнений общего вида. Метод
Тема 2. Арифметическое n-мерное векторное пространство. Линейная зависимость и независимость системы векторов.
Тема 3. Матрицы. Операции над матрицами. Обратная матрица.
Тема 4. Определители, их свойства и вычисление.
Тема 5. Правило Крамера и матричный способ решения системы линейных уравнений.
Слайд 7Темы раздела аналитическая геометрия
Тема 6. Элементы векторной алгебры.
Тема 7. Простейшие
Тема 8. Уравнения прямой на плоскости и в пространстве.
Тема 9. Уравнения плоскости в пространстве.
Тема 10. Взаимное расположение прямых и плоскостей.
Слайд 8Система линейных уравнений общего вида. Метод Жордана-Гаусса решения системы линейных
Тема 1
Слайд 9Система линейных уравнений.
Понятие системы линейных уравнений
Понятие совместной и несовместной системы, равносильные системы.
Элементарные преобразования системы, их основное свойство.
Система линейных уравнений базисного вида. Общее, частное, базисное, опорное решения СЛУ.
Слайд 10Определения.
О.1 Линейным уравнением (ЛУ) от n-переменных называется выражение вида:
или
О.2 Решением уравнения называется упорядоченный набор n вещественных чисел ,
при подстановке которых в уравнение вместо неизвестных соответственно, уравнение превращается в верное числовое равенство.
О.3 Системой линейных уравнений (СЛУ) называется совокупность ЛУ вида:
или
О.4 Решением СЛУ называется упорядоченный набор n вещественных чисел ,
являющийся решением каждого из m уравнений, входящих в систему.
Слайд 12Определения.
О.7 СЛУ называется совместной, если она имеет хотя бы одно решение,
Совместная система называется определенной, если она имеет единственное решение и неопределенной, если имеет более одного решения.
СЛУ называется однородной, если все ее свободные члены равны нулю.
О.8 Две системы линейных уравнений от одинакового числа неизвестных называются равносильными, если множества их решений совпадают.
Слайд 13О.9 Элементарными преобразованиями СЛУ называются следующие преобразования:
а) перестановка местами i-го и
б) умножение на число λ ≠ 0 обеих частей i-го уравнения;
в) прибавление к левой и правой частям i-го уравнения соответствующих частей j –го уравнения, умноженных на число λ;
г) удаление из системы нулевого уравнения:
.
Т.1 Элементарные преобразования переводят СЛУ в равносильную ей систему.
Слайд 15Определения.
О.10 Переменная в СЛУ называется базисной, если она
Говорят, что СЛУ имеет базисный вид, если в каждом уравнении выделена базисная переменная.
В системе базисного вида переменные, не являющиеся базисными, будем называть свободными переменными.
Слайд 17Определения.
О.11 Общим решением СЛУ называют множество упорядоченных наборов
Частное решение СЛУ получается из общего путем придания свободным переменным конкретных действительных значений.
О.12 Частное решение, в котором свободные переменные равны 0, называют базисным.
О.13 Базисное неотрицательное решение называют опорным.
Слайд 18Метод Жордана-Гаусса решения СЛУ
Приведение системы линейных уравнений к базисному виду методом
Алгоритм метода Жордана-Гаусса.
Анализ работы по методу Жордана-Гаусса.
Преобразование однократного замещения.
Однородные системы линейных уравнений.
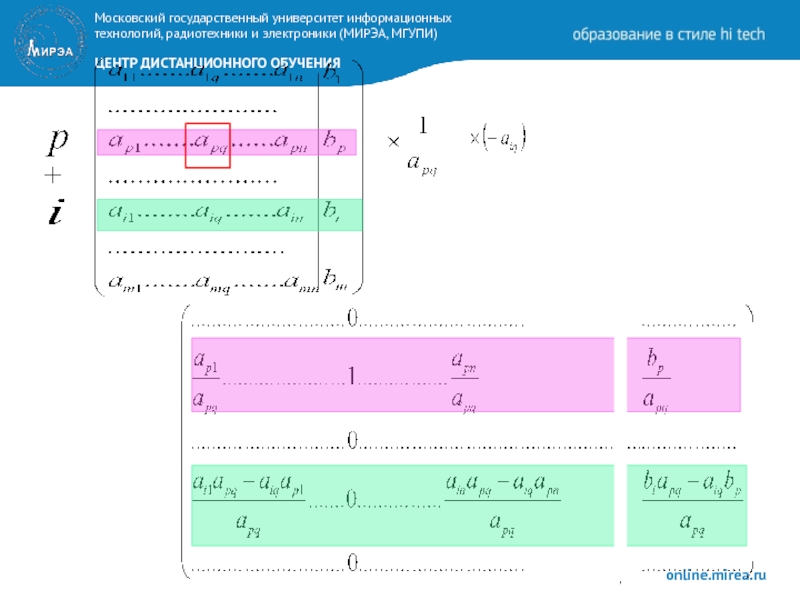
Слайд 21Формулы преобразований Жордана – Гаусса:
Элементы разрешающей строки делятся на разрешающий элемент
Элементы
Остальные элементы расширенной матрицы преобразуются по ” правилу прямоугольника”
Слайд 23Свойства преобразований Ж-Г.
Л 2.1. Преобразования Жордана - Гаусса переводят
Л 2.2. Если в разрешающей строке стоит 0, то соответствующий ему столбец не изменится при преобразовании Жордана - Гаусса.
Л 2.3. При преобразовании Жордана - Гаусса число базисных переменных не уменьшается.
Л 2.4. Если в разрешающем столбце стоит 0, то соответствующая ему строка расширенной матрицы не меняется при преобразовании Жордана - Гаусса.
Слайд 24Алгоритм Жордана – Гаусса.
Выберем уравнение, не содержащее базисной переменной. (Иначе СЛУ
Выберем в нем разрешающий элемент и сделаем шаг преобразований Жордана - Гаусса.
Преобразования проводим, пока в уравнениях без базисной переменной можно найти разрешающий элемент.
Получим два возможных исхода:
а) в каждом уравнении есть базисная переменная - тогда СЛУ приведена к базисному виду;
б) есть уравнение без базисной переменной, в котором нельзя выбрать разрешающий элемент:
Если в = 0, то это уравнение можно вычеркнуть из системы.
Если в ≠ 0, то уравнение не имеет решений, система несовместна.
Слайд 26Арифметическое n-мерное векторное пространство. Линейная зависимость и независимость
Тема 2
Слайд 27Арифметическое n-мерное векторное пространство.
Действия с арифметическими векторами,
Понятие линейной зависимости и линейной независимости системы векторов. Основные свойства линейной зависимости.
Векторная запись системы линейных уравнений.
Слайд 28Определения
О.5.1 Арифметическим вектором размерности n называется упорядоченный набор
О.5.2 Суммой векторов
и
называется вектор
Произведением вектора на число называется вектор
Слайд 29Т.5.1 Выше перечисленные операции обладают
сложение коммутативно, т.е.
сложение ассоциативно, т.е.
существует нулевой вектор , такой, что
существует противоположный вектор , такой , что
умножение унитарно, т.е.
умножение ассоциативно, т.е.
умножение дистрибутивно относительно сложения векторов, т.е.
умножение дистрибутивно относительно сложения чисел, т.е.
Слайд 30
О.5.3 Множество V , на котором заданы операции сложения и умножения
(1-8) теоремы 5.1. называется векторным (или линейным) пространством (над R). Элементы векторного пространства называют векторами.
Л.5.2 Для произвольных векторов справедливы равенства:
Слайд 31Определения
О.5.4 Линейной комбинацией векторов
называется выражение вида
или
Числа называются коэффициентами линейной комбинации.
О.5.5 Линейная комбинация называется тривиальной, если все коэффициенты в этой комбинации равны 0.
Слайд 32
О.5.5 Упорядоченный набор векторов называется системой векторов.
О.5.6 Система векторов
векторов этой системы
единственным образом – лишь в виде тривиальной комбинации, т.е.
О.5.7 Система векторов называется линейно зависимой , если нулевой вектор можно представить в виде линейной комбинации
векторов системы
не единственным образом, т.е.
Слайд 33Свойства линейной независимости и зависимости
С.1 Линейная независимость (зависимость) системы векторов не
С.2 Любая подсистема линейно независимой системы сама линейно независима.
С.3 Система, содержащая нулевой вектор, линейно зависима.
С.4 Система, содержащая два одинаковых вектора, линейно зависима.
С.5 Если система векторов содержит линейно зависимую подсистему, то сама система линейно зависима.
С.6 Система векторов линейно зависима, тогда и только тогда, когда хотя бы один вектор этой системы может быть представлен в виде линейной комбинации остальных векторов.
С.7 Если при добавлении к линейно независимой системе векторов какого-нибудь вектора получается линейно зависимая система, то добавленный вектор линейно выражается через остальные векторы новой системы.
Слайд 35Базис и ранг системы векторов
Базис системы векторов. Теорема о двух
Ранг системы векторов, его свойства. Ранг матрицы.
Вычисление ранга и нахождение базиса системы векторов.
Разложение векторов, не входящих в базис, по базисным векторам.
Слайд 36Определения
О.6.1. Подсистема Т:
S: называется системой образующих для S, если каждый вектор системы S линейно выражается (представляется в виде линейной комбинации) через векторы системы Т.
О.6.2. Базис системы S – это система ее образующих Т, являющаяся линейно независимой системой.
Теорема о двух базисах
Т.6.1. Число векторов в любом базисе данной системы векторов одно и то же.
Слайд 37 О.6.3.Рангом системы векторов называется число векторов в любом базисе этой
Л.5.2. Если к базису Т системы S добавить произвольный вектор , то полученная система будет линейно зависимой.
Л.5.3. Если из базиса Т удалить какой-либо вектор, то полученная система не будет системой образующих.
Слайд 38Ранг и его свойства
С.1. Ранг системы векторов – это максимальное число
С.2. Ранг системы векторов - это минимальное число элементов в системе образующих.
С.3. Ранг системы векторов не меняется при произвольной перестановке векторов системы.
С.4. Ранг системы векторов не меньше ранга любой ее подсистемы (свойство монотонности).
С.5. Ранг системы векторов не изменится, если к системе добавить (или удалить) произвольную линейную комбинацию векторов системы.
Слайд 39О.6.4. Рангом матрицы А мы будем называть ранг системы ее столбцов,
T.6.4. Ранг матрицы не меняется при элементарных преобразованиях.
Слайд 40Алгоритм вычисления ранга и нахождения базиса
Составить матрицу, записав векторы системы в
Элементарными преобразованиями (Жордана - Гаусса) привести матрицу к базисному виду.
Определить номера базисных столбцов.
Векторы с соответствующими номерами образуют базис, а их число равно рангу системы.
Слайд 42Операции над матрицами.
Матрицы. Операции над матрицами, их свойства.
Единичная матрица.
Способы нахождение обратной матрицы.
Матричные уравнения. Их решение.
Слайд 43Определения.
О.9.1 Матрицей размерности n x m называется таблица, состоящая из n
Элемент матрицы, расположенный на пересечении
i-ой строки и j-го столбца матрицы, обозначается .
Множество всех матриц размером n x m будем обозначать .
Слайд 44На множестве определены линейные операции: сложение
О.9.2 Суммой матриц и называется матрица
, элементы которой вычисляются по правилу .
О.9.3 Произведением матрицы на число называется матрица
.
Слайд 45
Свойства операции сложения матриц:
С.1 Коммутативность
С.2 Ассоциативность
С.3 Существует нулевая матрица
С.4 существует противоположная матрица
такая, что
Свойства операции умножения на число:
С.5 Унитарность
С.6 Ассоциативность
С.7 Дистрибутивность относительно сложения матриц
С.8 Дистрибутивность относительно сложения чисел
Слайд 46О.9.4 Произведением матриц
размерности k x n, в i-ой строке, j- ом столбце которой расположен элемент , вычисляемый по правилу:
=
Слайд 47
О.9.5 Матрица называется квадратной порядка n, если число ее строк равно
Множество квадратных матриц обозначается .
О.9.6 Квадратная матрица E порядка n называется единичной, если для любой матрицы A порядка n выполняется .
или
Л.9.1 Ранг единичной матрицы равен её порядку.
Слайд 48
О.9.7 Матрица
Обратная матрица к матрице А обозначается
Т.9.2 Для квадратной матрицы А обратная матрица существует тогда и только тогда, когда ранг матрицы А равен ее порядку.
Слайд 49Алгоритм нахождения обратной матрицы:
Расширить матрицу А справа единичной матрицей
Элементарными преобразованиями строк матрицу (A|E) преобразовать к виду ( |S).
Переменой строк матрицу ( |E) преобразовать к виду (Е|В).
Матрица В равна матрице .
Базисного
вида
Базисного
вида
Слайд 51Определители, их свойства и вычисление
Определители 2-го и 3-го порядков.
Понятие минора
Понятие определителя n-го порядка, его свойства и вычисление.
Нахождение обратной матрицы с помощью алгебраических дополнений.
Слайд 52Определения.
О.11.1 Определителем матрицы 2-го порядка называется число вычисляемое по правилу
О.11.2
Слайд 53
О.11.3 Минором , дополнительным к элементу
О.11.4 Алгебраическим дополнением к элементу называется дополнительный минор, взятый со знаком :
i
j
Слайд 55Свойства определителей
С.1 Определитель транспонированной матрицы равен определителю исходной.
С.2 Если матрица содержит
С.3 При перестановке двух соседних строк определитель меняет знак на противоположный.
С.4 Если матрица содержит две одинаковые строки, то ее определитель равен 0.
С.5 Если все элементы строки матрицы умножить на число k, то и определитель умножится на k.
С.6 Если в матрице все элементы некоторой строки представляют собой суммы двух чисел, то определитель матрицы может быть представлен как сумма двух определителей, соответствующая строка которых содержит 1 и 2 слагаемые, остальные строки, как в исходном определителе.
С.7 Если к строке матрицы прибавить другую строку матрицы умноженную на число, то определитель не изменится.
С.8 Определитель единичной матрицы равен 1.
С.9 Величина определителя не изменяется при преобразованиях Жордана – Гаусса с разрешающим элементом 1.
Слайд 56Алгоритм вычисления определителя n-го порядка с помощью преобразований Жордана – Гаусса.
Вынесем
Сделаем преобразование Ж-Г с разрешающим элементом 1, полученным в i-ой строке, j-ом столбце.
Исходный определитель равен произведению на алгебраическое дополнение преобразованного определителя.
Повторим п.1-3 для преобразованного определителя, пока его порядок не станет равен 2 или не появится нулевая строка.
Слайд 57
Л.12.1 Сумма произведений всех элементов строки (столбца) квадратной матрицы на алгебраические
или
Слайд 58Алгоритм вычисления с помощью алгебраических дополнений.
Вычислим определитель исходной
если , то для А не существует;
если , то
Построим матрицу , заменив каждый элемент матрицы А его алгебраическим дополнением.
Транспонируя матрицу , получим матрицу
Умножим матрицу на число
, тем самым получим
матрицу, обратную к А.
Слайд 60Различные способы решения квадратных СЛУ
Правило Крамера решения квадратных систем линейных уравнений.
Слайд 62Пусть ΔJ – определитель матрицы, полученной из матрицы А заменой j–го
Тогда, если , то СЛУ имеет единственное решение, которое определяется по формулам:
Слайд 65Темы раздела аналитическая геометрия
Тема 6. Элементы векторной алгебры.
Тема 7. Простейшие
Тема 8. Уравнения прямой на плоскости и в пространстве.
Тема 9. Уравнения плоскости в пространстве.
Тема 10. Взаимное расположение прямых и плоскостей.
Слайд 67Элементы векторной алгебры.
Линейные операции над геометрическими векторами.
Система координат на плоскости
Декартова система координат. Скалярное произведение и его свойства. Скалярное произведение в координатах. Угол между векторами. Длина отрезка.
Слайд 69Простейшие задачи аналитической геометрии в декартовой системе координат
Координаты вектора
Отрезок. Деление отрезка в данном отношении.
Скалярное произведение в координатах. Угол между векторами.
Длина отрезка.
Условия коллинеарности и перпендикулярности 2 векторов, компланарности 3 векторов.
Слайд 71Уравнения прямой на плоскости и в пространстве.
Уравнение прямой по точке
Уравнение прямой по двум точкам.
Уравнение прямой на плоскости по точке и нормальному вектору.
Общее уравнение прямой на плоскости. Задание полуплоскости.
Взаимное расположение прямых на плоскости.
Слайд 72Пусть прямая проходит через точку
параллельно вектору
Этот вектор называется направляющим вектором
Уравнение прямой по точке и направляющему вектору
Слайд 73и рассмотрим вектор
Выберем на прямой произвольную точку
Уравнения прямой могут быть
канонические уравнения прямой
Слайд 74Пусть прямая проходит через две точки
Выберем на прямой произвольную точку
Уравнения
уравнения прямой,
проходящей через две точки
Слайд 75Уравнение прямой на плоскости по точке и нормальному вектору.
Выберем на плоскости
Тогда и
Тогда скалярное произведение этих векторов должно быть равно нулю:
Распишем его в координатах:
Слайд 78Уравнения плоскости в пространстве.
Уравнение плоскости по точке и двум направляющим
Уравнение плоскости по 3-м точкам.
Уравнение плоскости по точке и нормальному вектору.
Общее уравнение плоскости. Линейное неравенство с тремя переменными.
Слайд 79Пусть плоскость проходит через точку
параллельно векторам
Возьмем точку на плоскости и рассмотрим вектор
Уравнение плоскости по точке и двум направляющим векторам
Уравнение плоскости может быть получено из условия компланарности этого вектора и двух направляющих векторов плоскости:
Слайд 81Пусть задана плоскость, проходящая через три точки:
Тогда уравнение этой плоскости можно
Уравнение плоскости по трем точкам
уравнение плоскости, проходящей
через точку и параллельно двум векторам
Слайд 83Пусть плоскость Р, проходит через заданную точку
и перпендикулярна вектору
Этот вектор называется
Выберем на плоскости произвольную точку
Тогда
Тогда скалярное произведение этих векторов
должно быть равно нулю:
Распишем его в координатах:
и
Слайд 85Раскроем скобки в предыдущем уравнении:
Обозначим:
Общее уравнение плоскости
общее уравнение плоскости
Слайд 87Взаимное расположение прямых и плоскостей.
Взаимное расположение прямых в пространстве.
Взаимное расположение
Взаимное расположение плоскостей пространства.
Различные уравнения прямой и плоскости.
Слайд 88Пусть заданы две прямые
Острый угол между этими прямыми находится из скалярного
угол между прямыми
в пространстве
Слайд 90Пусть прямая задана уравнением:
И пусть плоскость
Взаимное расположение прямой и плоскости
Тогда направляющий вектор прямой
нормальный вектор плоскости
точка принадлежащая прямой
Слайд 91Возможные случаи ориентации прямой и плоскости:
Если прямая параллельна плоскости, то
Если прямая
Прямая пересекает плоскость в одной точке, тогда
Если прямая перпендикулярна плоскости, то



![Базы данных, информационно-справочные и поисковые системыСправочно-информационная система Гарант, Консультант.Электронная библиотечная система КнигаФонд [Электронный ресурс]. Электрон.](/img/tmb/5/465455/436b6815ca1cb245383300dcc888ca1c-800x.jpg)