- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Цикломатика графов презентация
Содержание
- 1. Цикломатика графов
- 2. Свойства графов, которые мы будем изучать в
- 3. 4.1. Цикломатическое число
- 4. Определение
- 5. Цикловые ребра и перешейки Назовем ребро цикловым,
- 6.
- 7. Свойства цикломатического числа
- 8.
- 9. 4.2. Деревья
- 10. Определения Связный граф без циклов называется деревом
- 11. Свойства дерева
- 12.
- 13. Свойство 5. Добавление ребра (разумеется, без добавления
- 14. 4.3. Каркасы
- 15. Определение Каркас связного графа является деревом.
- 16. Алгоритм нахождения каркаса Алгоритм является модификацией волнового
- 17.
- 18.
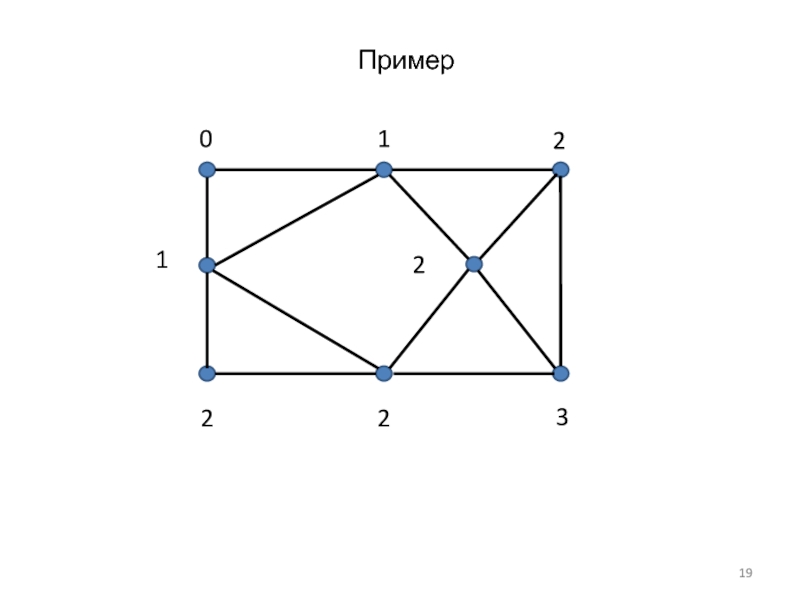
- 19. Пример 0 1 1 2 2 2 2 3
- 20. Кратчайший каркас графа
- 21. Алгоритм Прима
- 22. Robert C. Prim (b. 1921) along with
- 23.
- 24.
- 25.
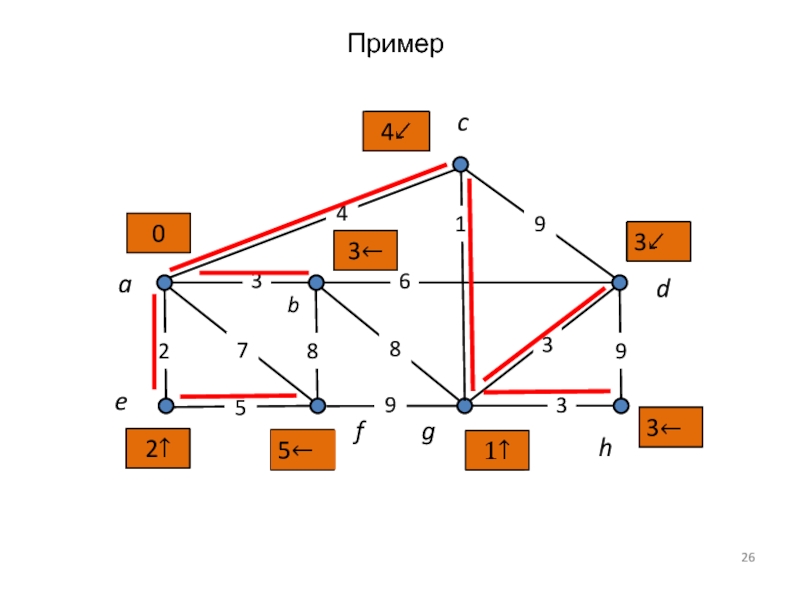
- 26. f
- 28. Теорема о хорде каркаса
- 29.
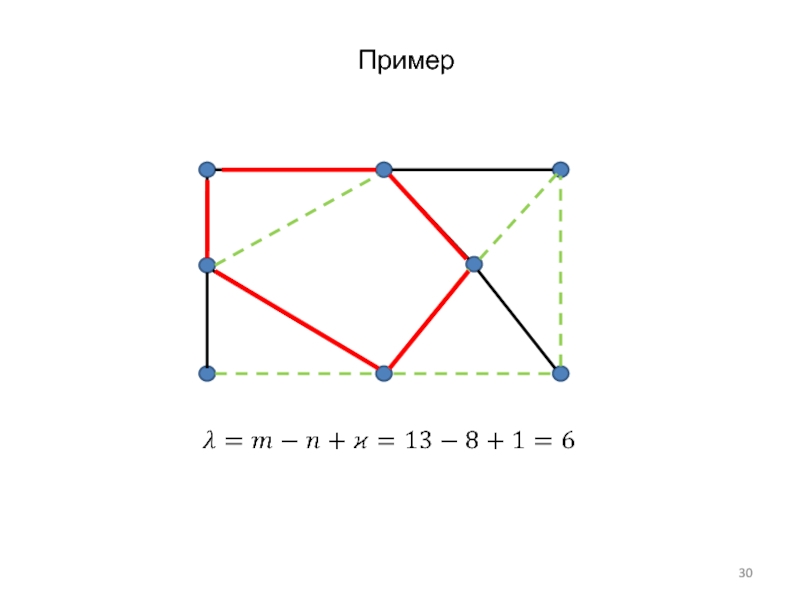
- 30. Пример
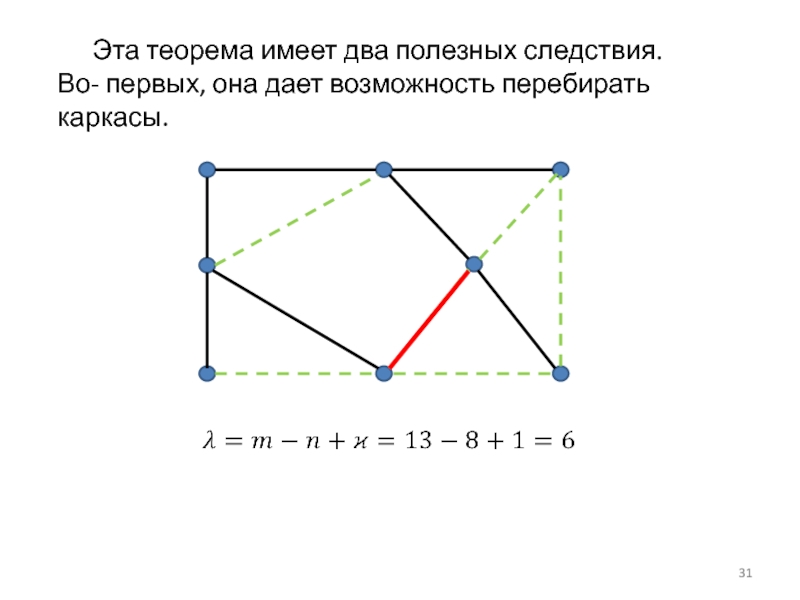
- 31. Эта теорема имеет два полезных следствия. Во- первых, она дает возможность перебирать каркасы.
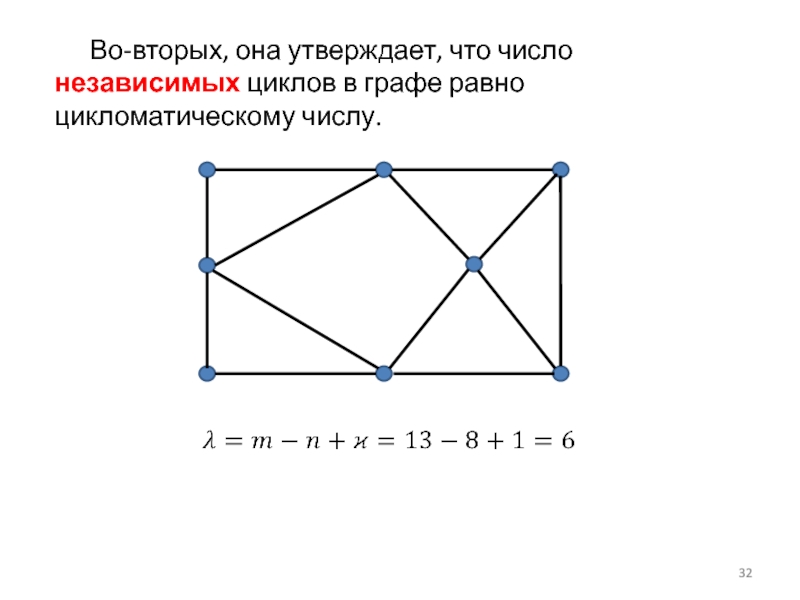
- 32. Во-вторых, она утверждает, что число независимых циклов в графе равно цикломатическому числу.
- 33. Каждому суграфу G ’=(V,E ’) графа G=(V,E)
- 34. Однореберные суграфы линейно независимы, а любой суграф
- 35. В этом разделе цикл определяется как суграф,
- 36. 2 4
Свойства графов, которые мы будем изучать в данной главе, присущи графам общего вида и не зависят от ориентации.
Слайд 2Свойства графов, которые мы будем изучать в данной главе, присущи графам
общего вида и не зависят от ориентации.
Слайд 5Цикловые ребра и перешейки
Назовем ребро цикловым, если оно содержится хотя бы
в одном цикле; в противном случае назовем его перешейком (bridge).
Точкой сочленения (шарниром) называется вершина, при
удалении которой число компонент увеличивается.
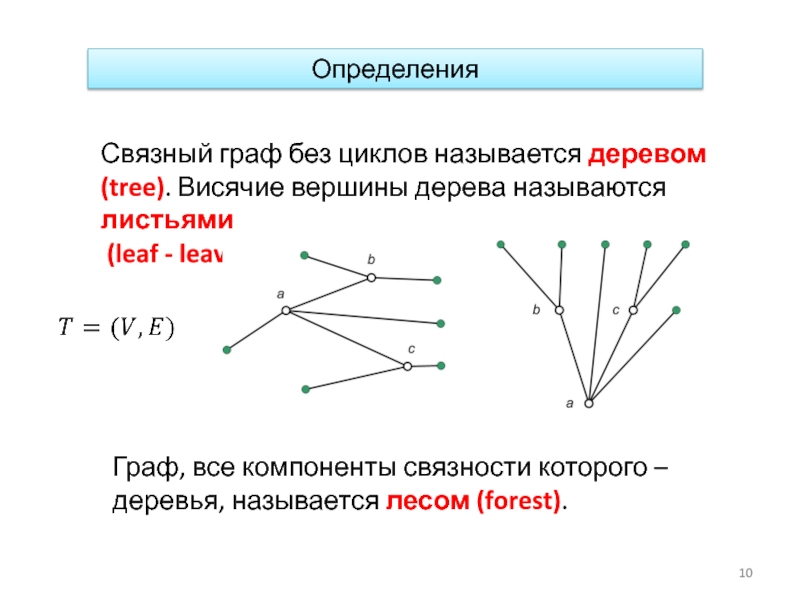
Слайд 10Определения
Связный граф без циклов называется деревом (tree). Висячие вершины дерева называются
листьями
(leaf - leaves).
(leaf - leaves).
Граф, все компоненты связности которого – деревья, называется лесом (forest).
Слайд 13Свойство 5. Добавление ребра (разумеется, без добавления
вершины) приводит к увеличению
λ на единицу,
то есть к появлению цикла.
Свойство 6 проверяется непосредственно: все вершины дерева,
кроме висячих, являются точками сочленения.
Свойство 7. В любом графе с числом вершин ≥2 есть по крайней
мере две вершины, не являющиеся точками сочленения.
Для дерева это висячие вершины.
то есть к появлению цикла.
Свойство 6 проверяется непосредственно: все вершины дерева,
кроме висячих, являются точками сочленения.
Свойство 7. В любом графе с числом вершин ≥2 есть по крайней
мере две вершины, не являющиеся точками сочленения.
Для дерева это висячие вершины.
Слайд 16Алгоритм нахождения каркаса
Алгоритм является модификацией волнового алгоритма нахождения кратчайшей цепи.
Шаг 1.
Выберем произвольную вершину и пометим ее меткой 0.
Шаг 2. Все непомеченные вершины, смежные с вершинами, имеющими метку k, помечаем меткой k + 1. Разметка продолжается до тех пор, пока все вершины не будут помечены. При такой разметке метки смежных вершин не могут отличаться более чем на единицу.
Шаг 2. Все непомеченные вершины, смежные с вершинами, имеющими метку k, помечаем меткой k + 1. Разметка продолжается до тех пор, пока все вершины не будут помечены. При такой разметке метки смежных вершин не могут отличаться более чем на единицу.
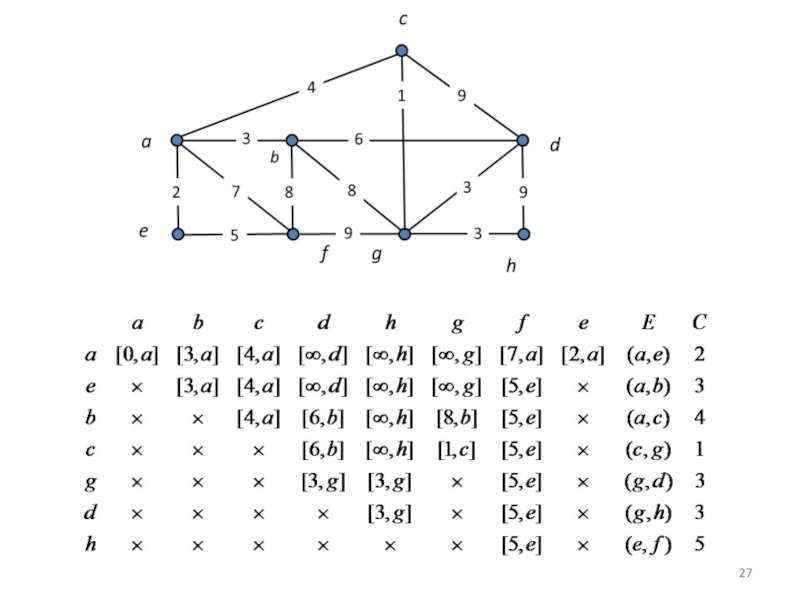
Слайд 22Robert C. Prim (b. 1921) along with coworker Joseph Kruskal developed
two different algorithms (see greedy algorithm) for finding a minimum spanning tree in a weighted graph, a basic stumbling block in computer network design. His self-named algorithm, Prim's algorithm, was originally discovered in 1930 by mathematician Vojtěch Jarník and later independently by Prim in 1957. It was later rediscovered by Edsger Dijkstra in 1959. It is sometimes referred to as the DJP algorithm or the Jarník algorithm
en.wikipedia.org/wiki/Robert_C._Prim
Слайд 31 Эта теорема имеет два полезных следствия.
Во- первых, она дает возможность перебирать
каркасы.
Слайд 32 Во-вторых, она утверждает, что число независимых циклов в графе равно цикломатическому
числу.
Слайд 33Каждому суграфу G ’=(V,E ’) графа G=(V,E) взаимно однозначно
соответствует подмножество ребер
E ’⊆E ; каждое E ‘ задается
вектором
вектором
,
у которого
Далее суграфом называют и E ‘, и
0⊕0=0, 1⊕0=1, 0⊕1=1, 1⊕1=0
Слайд 34Однореберные суграфы
линейно независимы, а любой суграф есть их линейная комбинация
=
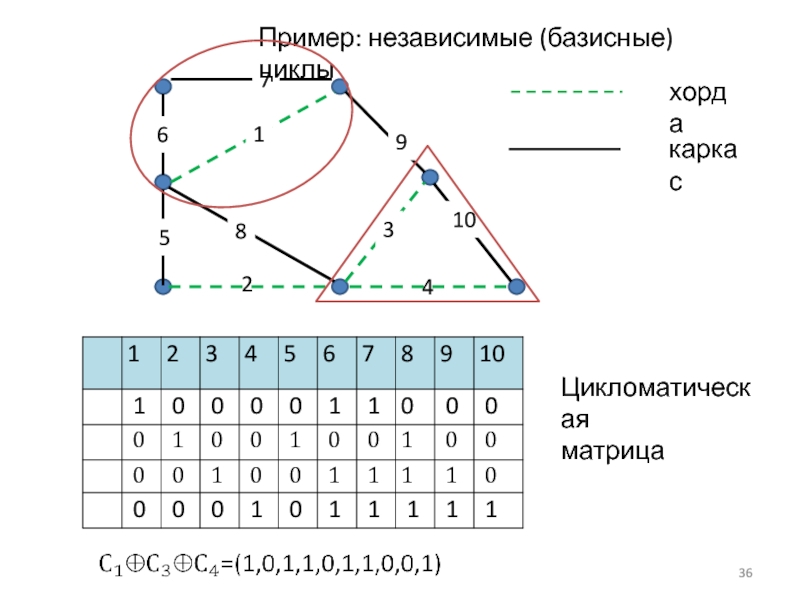
Пример:
сумма суграфов (1,1,0,1) ⊕(1,0,1,1)=(0,1,1,0)
Слайд 35В этом разделе цикл определяется как суграф, все вершины ко-
торого имеют
четные валентности. Сумма двух циклов есть цикл
(не обязательно цикл в обычном понимании: это могут быть два
цикла без общих вершин). Множество циклов образует линейное
пространство.
(не обязательно цикл в обычном понимании: это могут быть два
цикла без общих вершин). Множество циклов образует линейное
пространство.
Пусть теперь T -- некоторый каркас графа G. Каждой хорде этого
каркаса поставим в соответствие тот единственный цикл, который
она образует вместе с некоторыми ребрами T, и тем самым полу-
чим систему из λ(G ) циклов. Элементы этой системы линейно не-
зависимы и образуют базис пространства циклов размерности λ(G ).
Любой другой цикл может быть получен как линейная комбинация
независимых (базисных) циклов.
