- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Фрактали презентация
Содержание
- 1. Фрактали
- 2. Для тих, хто любить математику, для
- 4. Тип проекту: інформаційний. Мета проекту: Довести,
- 5. Задачі проекту: Закріпити знання отримані в
- 6. Етапи проведення проекту: «Проблема». (вересень) Формулювання проблеми,
- 7. «Планування» (проектування роботи в кінці вересня). Обговорення
- 8. «Пошук інформації». (жовтень). Самостійна робота з виконання
- 9. Група «Істориків» Все, що створено людиною,
- 10. Об'єкти, які тепер називаються фракталами, досліджувались
- 11. Ідею "рекурсивної самоподібності" було висунуто філософом Лейбніцом,
- 12. Ґеорг Кантор навів приклади підмножин дійсних чисел
- 13. Існують три поширені методи створення (генерування) фракталів:
- 14. Тетрікс (tetrix) – просторовий аналог трикутника Серпінського
- 15. Т-Квадрат
- 16. Другий метод — рекурентні відношення, це фрактали, що
- 17. палаючий корабель Цілий фрактал Багаторазове збільшення "кораблика" заднього плану
- 18. Третій метод — випадкові процеси, це фрактали, що
- 19. Приклад броунівського дерева Броунівське дерево, вирощене з мідного купорусу та броунівське дерево.
- 20. Група «Математиків» Фрактали можна класифікувати відповідно
- 21. Майже самоподібність — Слабка форма самоподібності; фрактал виглядає
- 22. Статистична самоподібність — Це найслабкіша форма самоподібності;
- 23. Слід зазначити, що не всі самоподібні об'єкти
- 24. Група «Науковців» В математиці концепція фракталів має
- 25. ФРАКТАЛИ НА КУХНІ: Можна припустити, що форма
- 26. Фрактальні морскі істоти: *
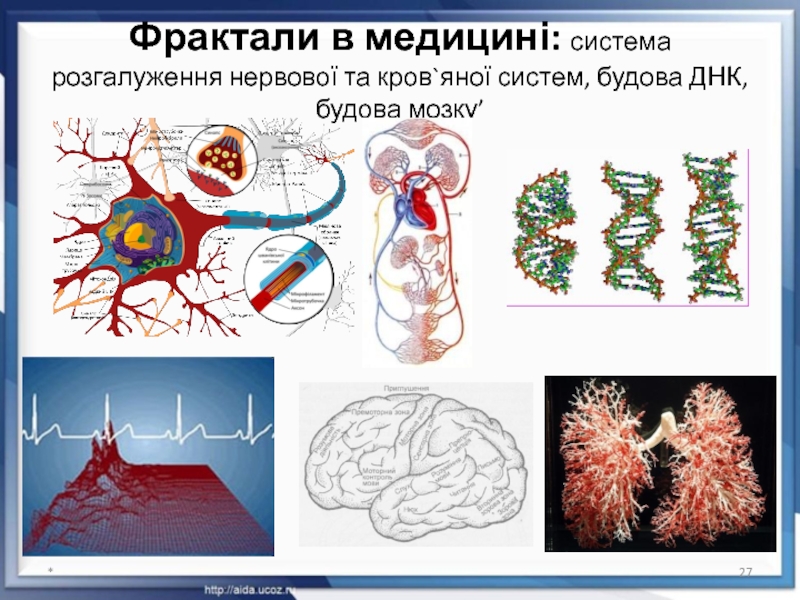
- 27. Фрактали в медицині: система розгалуження нервової та кров`яної систем, будова ДНК, будова мозку’ *
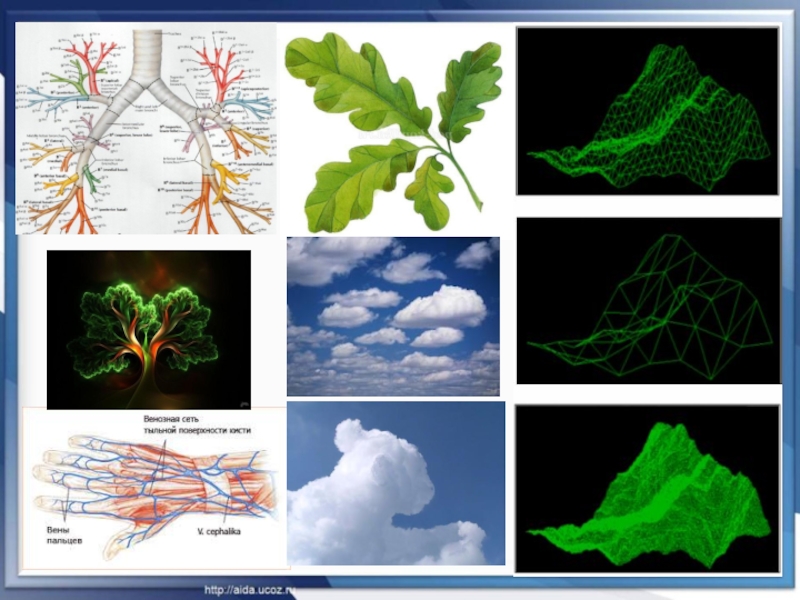
- 28. Географічні фрактали: гори, блискавки, берегові лінії островів і багато іншого. *
- 29. Літературні фрактали. Серед літературних
- 30. *
- 31. Група «Мистецтвознавців» Жодна сучасна креативна особистість не
- 32. У наш час все більше і
- 33. Сучасна поліграфія має надзвичайно широкий спектр послуг
- 34. Як ви вже знаєте, зараз досить
- 35. А інші аспекти творчо ї діяльності чи
- 36. Галерея фракталів
- 50. Дякуємо за увагу !
Слайд 2Для тих, хто любить математику, для тих, хто думає, що він любить
Слайд 4Тип проекту: інформаційний.
Мета проекту:
Довести, що фрактали є красивими та наглядними
Побачити світ фракталів навколо нас.
Розглянути види та способи побудови фракталів.
Розширити вміння та навики пошуку додаткової інформації, роботи з комп`ютером.
Слайд 5Задачі проекту:
Закріпити знання отримані в процесі навчання на уроках математики,
Розширити відомості учнів про історичне походження фракталів, про видатних математиків, минулого сторіччя, що внесли свої знання в тему фракталів.
Виховувати вміння працювати у групі, знаходячи компроміси та спільні рішення однієї проблеми.
Розвивати соціальні компетентності учнів, їх вміння презентувати свій «продукт» роботи.
Слайд 6Етапи проведення проекту:
«Проблема». (вересень)
Формулювання проблеми, яка стала темою проекту. Формування груп:
1-а «Історики»;
2-а «Математики»;
3-я «Науковці»;
4-а « Мистецтвознавці».
Слайд 7«Планування»
(проектування роботи в кінці вересня).
Обговорення та складання плану роботи кожною групою
«Історики» отримали завдання зібрати відомості про дослідження та виникнення поняття «фрактал», а також про вчених, які зробили внесок у розвиток цієї теми.
«Математики» повинні донести всю теоретичну основу знань відому сучасній науці з цієї теми.
«Науковці» отримали завдання знайти різноманітні науки, сфери життя людини та в оточуючому середовищі де фрактали несуть наукову ідею .
«Мистецтвознавці» отримали завдання знайти інші науки чи сфери людської діяльності, мистецтва де б використовували красу фракталів .
Слайд 8«Пошук інформації». (жовтень). Самостійна робота з виконання завдань.. «Продукт». (перша та друга декади
Слайд 9 Група «Істориків»
Все, що створено людиною, обмежено площинами. Коли зустрічається об’єкт
Фракта́л (лат. fractus — подрібнений, дробовий) — нерегулярна, самоподібна структура. В широкому розумінні фрактал означає фігуру, малі частини якої в довільному збільшенні є подібними до неї самої.
Слайд 10 Об'єкти, які тепер називаються фракталами, досліджувались задовго до того, як
Килим Серпінського
Слайд 11Ідею "рекурсивної самоподібності" було висунуто філософом Лейбніцом, який також розробив багато
мал.2 а б в
Слайд 12Ґеорг Кантор навів приклади підмножин дійсних чисел із незвичними властивостями —
мал.3
Слайд 13Існують три поширені методи створення (генерування) фракталів: Перший метод — ітераційні функції, які
сніжинка Коха
Килим Серпінського
трикутник Серпінського
крива Коха
крива дракона
Слайд 16Другий метод — рекурентні відношення, це фрактали, що визначаються рекурентним відношенням у
множина Мандельброта
фрактал Ляпунова.
Слайд 18Третій метод — випадкові процеси, це фрактали, що генеруються з використанням стохастичних,
Слайд 19Приклад броунівського дерева
Броунівське дерево,
вирощене з мідного купорусу
та броунівське дерево.
Слайд 20Група «Математиків»
Фрактали можна класифікувати відповідно до їхньої самоподібності.
Розрізняють три
Точна самоподібність — Це найсильніший тип самоподібності; фрактал виглядає однаково при любих збільшеннях. У фракталів, згенерованих з використанням ітераційних функцій, часто виявляється точна самоподібність.
Слайд 21Майже самоподібність — Слабка форма самоподібності; фрактал виглядає приблизно (але не точно)
Слайд 22 Статистична самоподібність — Це найслабкіша форма самоподібності; фрактал має чисельні або статистичні
*
Слайд 23Слід зазначити, що не всі самоподібні об'єкти є фракталами; наприклад, числова
*
Слайд 24Група «Науковців»
В математиці концепція фракталів має геометричну сутність, яка представляє систему
Багато природних об'єктів також самоподібні і складаються з повторюваних елементів різних розмірів. Очевидні приклади – дерева, кущ, колонії коралів. Навіть більш яскравим прикладом є суцвіття укропу, "парасолька", яка в свою чергу складається з маленьких парасольок. На рисунку 1. а суцвіття рослин, родини umbelliferae і на рисунку 1.b це схема, побудована з використанням фрактальної графіки.
Рис. 1 а Рис. 1 б.
Слайд 25ФРАКТАЛИ НА КУХНІ:
Можна припустити, що форма і структура будь-яких природних об'єктів,
Знайшли безліч природних об'єктів, структура, яких схожа на фрактали: гілки дерев, які повторюють великі гілки стовбура, сніжинки, судини крові і нерви, карта півкуль головного мозку і будь-які карти, і так далі.
*
Слайд 27Фрактали в медицині: система розгалуження нервової та кров`яної систем, будова ДНК,
*
Слайд 29Літературні фрактали. Серед літературних творів є ті, які мають
*