- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Монотонность и экстремумы функции презентация
Содержание
- 1. Монотонность и экстремумы функции
- 2. x2 > x1 ⇒ f (x2) >
- 3. Признак возрастания функции. Для того, чтобы функция
- 4. Определение. Точка х0 называется точкой максимума(max), если
- 5. Определение. Точка х0 называется точкой минимума(min), если
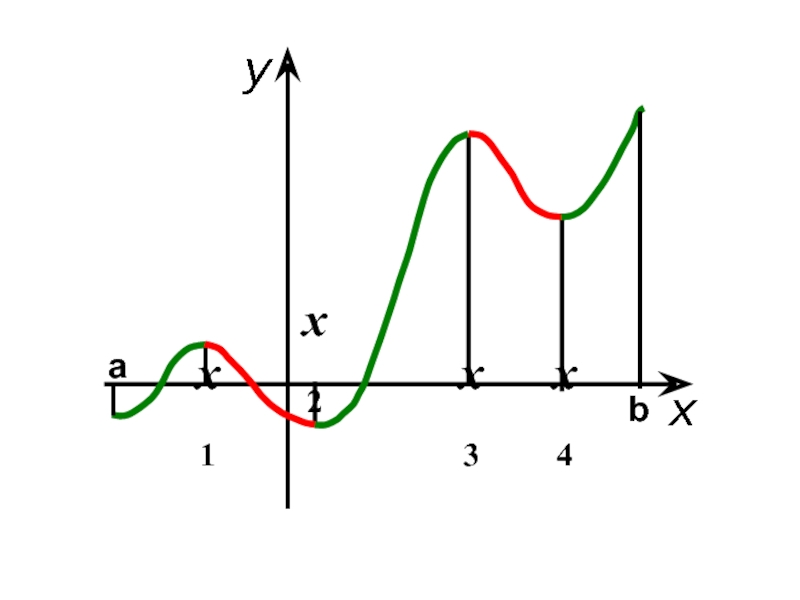
- 6. x1 x2 x3 x4
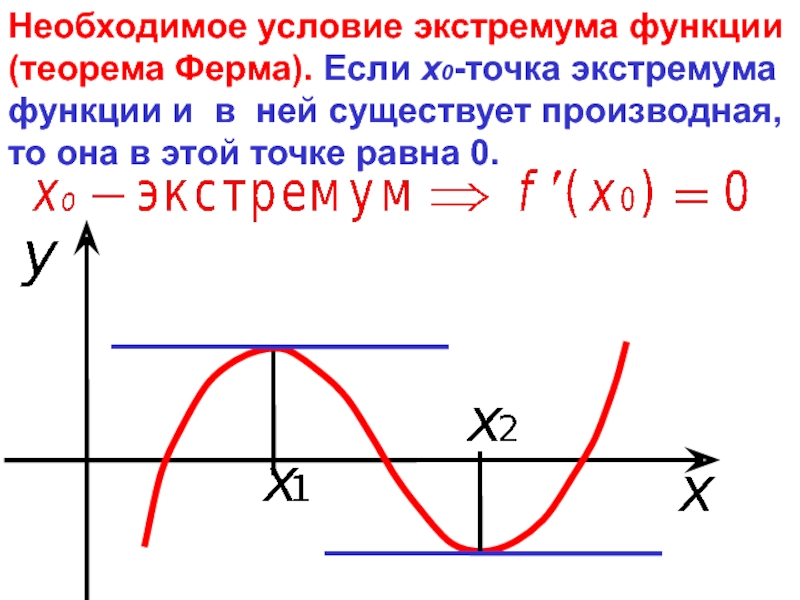
- 7. Необходимое условие экстремума функции (теорема Ферма). Если
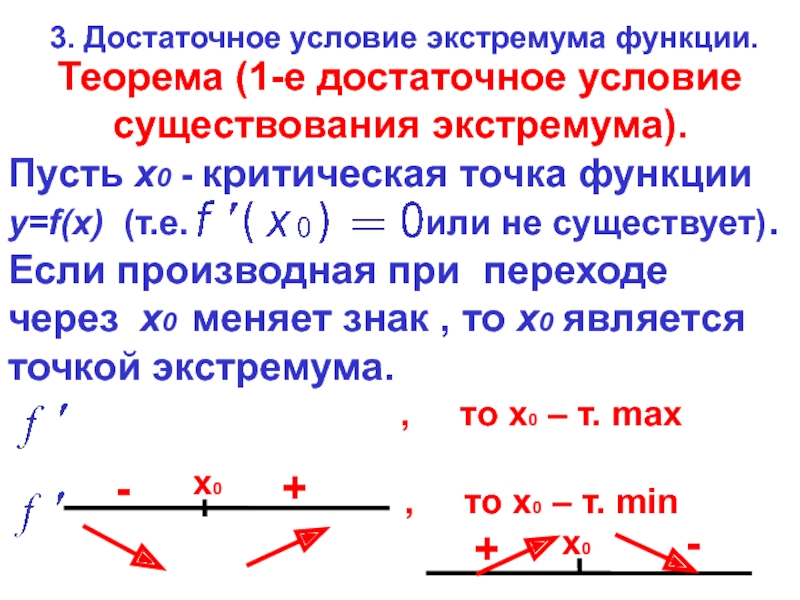
- 9. Теорема (1-е достаточное условие существования экстремума). Пусть
- 10. Схема исследования функции на монотонность и экстремумы.
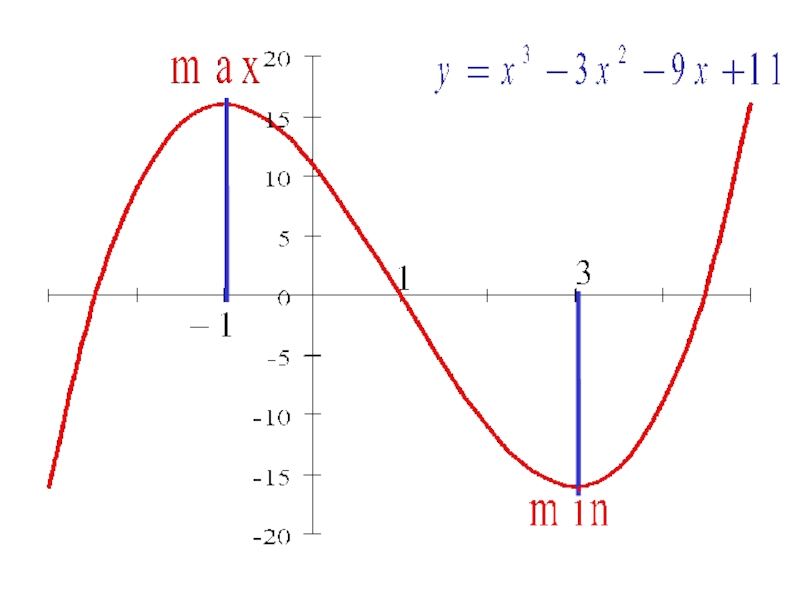
- 11. Пример. Исследовать функцию на монотонность,
- 13. Исследование на экстремум с помощью производных высших порядков.
- 14. Теорема (2-е достаточное условие существования экстремума). Пусть
- 15. Пример Функцию исследовать на точки экстремума по 2-му достаточному условию.
- 16. Задание на самоподготовку: 1) исследовать функцию на монотонность и экстремумы (2-мя способами) Дана функция
Слайд 1Тема 3/1. Монотонность и экстремумы функции.
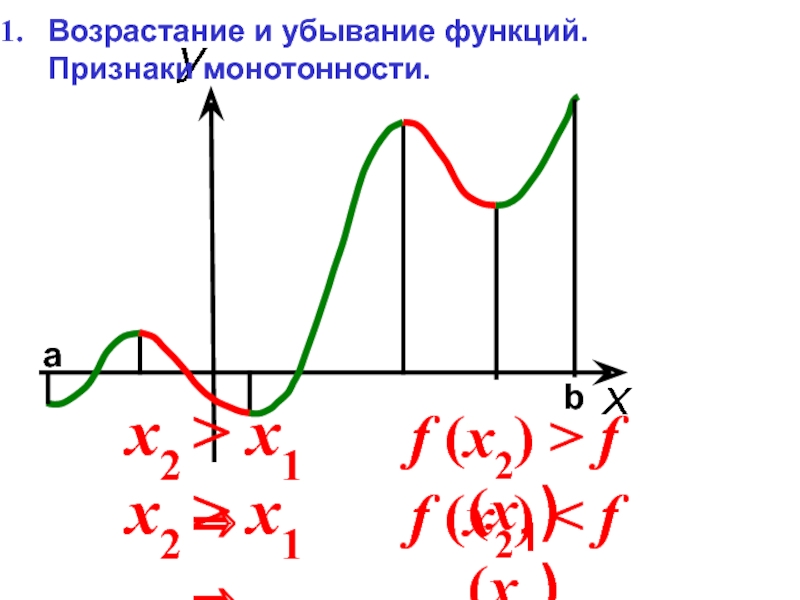
Возрастание и убывание функций. Признаки монотонности.
Точки
3. Достаточное условие экстремума.
Слайд 2x2 > x1 ⇒
f (x2) > f (x1)
x2 > x1 ⇒
f
Возрастание и убывание функций. Признаки монотонности.
Слайд 3Признак возрастания функции.
Для того, чтобы функция y=f(x) возраста-ла на промежутке, необходимо
Признак убывания функции.
Для того , чтобы функция y=f(x) убывала на промежутке, необходимо и достаточно, чтобы производная функции была отри-цательной на этом промежутке.
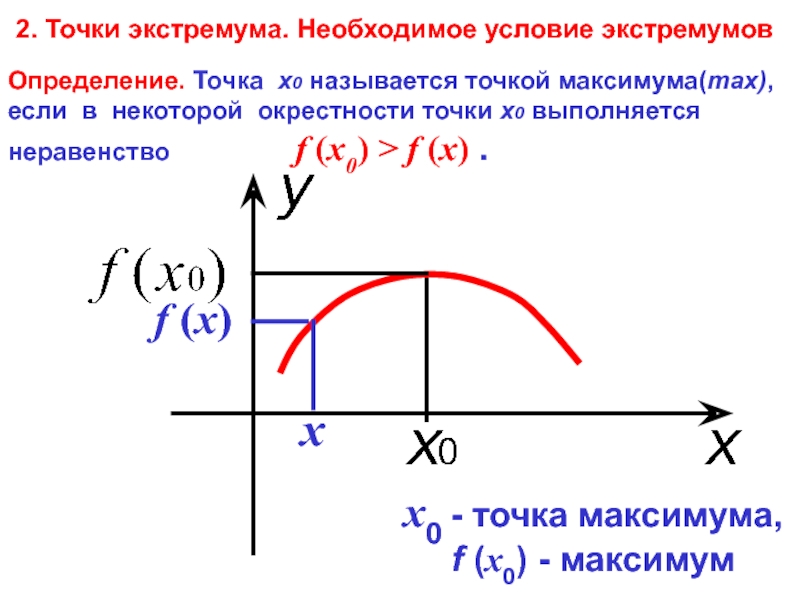
Слайд 4Определение. Точка х0 называется точкой максимума(max), если в некоторой окрестности точки
x0 - точка максимума, f (x0) - максимум
2. Точки экстремума. Необходимое условие экстремумов
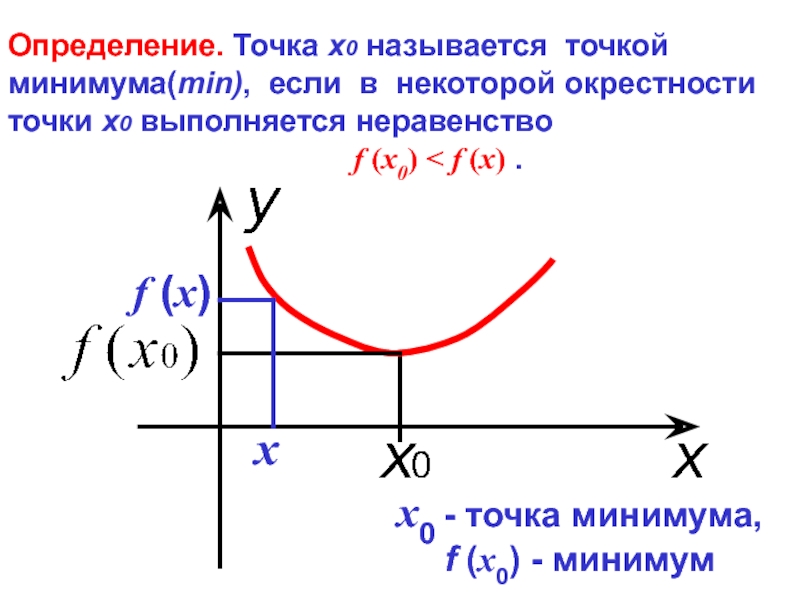
Слайд 5Определение. Точка х0 называется точкой минимума(min), если в некоторой окрестности точки
f (x0) < f (x) .
x0 - точка минимума, f (x0) - минимум
Слайд 7Необходимое условие экстремума функции
(теорема Ферма). Если х0-точка экстремума функции и в
Слайд 9Теорема (1-е достаточное условие существования экстремума).
Пусть x0 - критическая точка функции
Если производная при переходе через х0 меняет знак , то х0 является точкой экстремума.
3. Достаточное условие экстремума функции.
+
-
x0
, то х0 – т. max
x0
+
-
, то х0 – т. min
Слайд 10Схема исследования функции на монотонность и экстремумы.
1. Найти
2. Найти критические
(т.е. решить уравнение f ′ (x) = 0 )
3. Установить знаки производной при
переходе через критические точки и
определить точки экстремума.
4. Найти значения функции в точках
экстремума.
Слайд 14Теорема (2-е достаточное условие существования экстремума).
Пусть x0 - критическая точка функции,
Если вторая производная функции в точке х0 положительна , то х0 - точка минимума.
Если вторая производная функции в точке x0 отрицательна, то x0 - точка максимума.